Subsegments （线段树）

最新推荐文章于 2022-06-06 11:24:45 发布

原创最新推荐文章于 2022-06-06 11:24:45 发布 · 310 阅读

0 ·

CC 4.0 BY-SA版权

线段树专栏收录该内容

34 篇文章

订阅专栏

程序员Sasha需要在一个数组的每个固定长度的子段中找到恰好出现一次的最大元素。输入包含数组长度n和子段长度k，输出n-k+1行，每行对应一个子段中的唯一最大值。解题方法是采用双指针和线段树，线段树用于维护区间内出现一次的元素数量，并通过二分查找确定最大值。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

Subsegments

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

Programmer Sasha has recently begun to study data structures. His coach Stas told him to solve the problem of finding a minimum on the segment of the array in 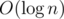, which Sasha coped with. For Sasha not to think that he had learned all, Stas gave him a new task. For each segment of the fixed length Sasha must find the maximum element of those that occur on the given segment exactly once. Help Sasha solve this problem.

Input

The first line contains two positive integers n and k (1 ≤ n ≤ 105, 1 ≤ k ≤ n) — the number of array elements and the length of the segment.

Then follow n lines: the i-th one contains a single number ai ( - 109 ≤ ai ≤ 109).

Output

Print n–k + 1 numbers, one per line: on the i-th line print of the maximum number of those numbers from the subarray ai ai + 1 … ai + k - 1that occur in this subarray exactly 1 time. If there are no such numbers in this subarray, print "Nothing".

Examples

input

Copy

output

Copy

1
3
2

input

Copy

output

Copy

4
Nothing
3

题目大意：一个序列，给出一个窗口大小为k，求每个窗口中只出现一次且最大的数是多少。

解题思路：双指针保证每次线段树中只有k个数被插入，然后线段树维护一下左右区间各有多少个只出现1次的数。

然后在线段树上二分，如果右区间有出现过一次的数就尽量走右区间，否则走左区间。

#include<bits/stdc++.h>
using namespace std;
#define inf 0x3f3f3f3f
#define pb(x) push_back(x)
 
const int N  = 1e5+5;
set<int>s;
map<int,int>mmp;
int a[N],b[N];
vector<int>v;
 
struct node
{
    int val,sz,kid;
}t[N*4];
 
void upd(int rt,int l,int r,int pos,int val)
{
    if(l==r)
    {
        t[rt].sz+=val;
        if(t[rt].sz==1)t[rt].kid=1;
        else t[rt].kid=0;
        return ;
    }
 
    int m=(l+r)>>1;
    if(pos<=m) upd(rt<<1,l,m,pos,val);
    else upd(rt<<1|1,m+1,r,pos,val);
    t[rt].kid=t[rt<<1].kid+t[rt<<1|1].kid;
    t[rt].val=t[rt<<1].val+t[rt<<1|1].val;
}
 
int ask(int rt,int l,int r)
{
    if(l==r)
    {
        return v[l-1];
    }
    int m=(l+r)>>1;
    if(t[rt<<1|1].kid!=0)
    {
        return ask(rt<<1|1,m+1,r);
    }
    else if(t[rt<<1].kid!=0)
    {
        return ask(rt<<1,l,m);
    }
    else return inf;
}
 
int main()
{
    int n,k;
    cin>>n>>k;
    for(int i=1; i<=n; i++)
    {
        scanf("%d",a+i);
        v.pb(a[i]);
    }
    sort(v.begin(),v.end());
    v.erase(unique(v.begin(),v.end()),v.end());
    for(int i=1;i<=n;i++)
    {
        b[i]=lower_bound(v.begin(),v.end(),a[i])-v.begin()+1;
    }
    int l=1,r=0;
    while(r<n)
    {
        if(r-l+1<k)
        {
            r++;
            upd(1,1,n,b[r],1);
        }
        else
        {
            upd(1,1,n,b[l],-1);
            l++;
        }
        if(r-l+1==k)
        {
            int tmp=ask(1,1,n);
            if(tmp==inf)puts("Nothing");
            else printf("%d\n",tmp);
        }
    }
}