You are given an array a consisting of n integers. A subarray (l, r) from array a is defined as non-empty sequence of consecutive elements al, al + 1, ..., ar.
The beauty of a subarray (l, r) is calculated as the bitwise AND for all elements in the subarray:
Your task is to calculate the summation of the beauty of all subarrays (l, r) (1 ≤ l ≤ r ≤ n):
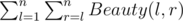
The first line contains an integer T, where T is the number of test cases.
The first line of each test case contains an integer n (1 ≤ n ≤ 105), where n is the size of the array a.
The second line of each test case contains n integers a1, a2, ..., an (1 ≤ ai ≤ 106), giving the array a.
For each test case, print a single line containing the summation of the beauty of all subarrays in the given array.
2 3 7 11 9 4 11 9 6 11
40 48
As input/output can reach huge size it is recommended to use fast input/output methods: for example, prefer to use scanf/printfinstead of cin/cout in C++, prefer to use BufferedReader/PrintWriter instead of Scanner/System.out in Java.
A bitwise AND takes two equal-length binary representations and performs the logical AND operation on each pair of the corresponding bits, by multiplying them. Thus, if both bits in the compared position are 1, the bit in the resulting binary representation is 1 (1 × 1 = 1); otherwise, the result is 0 (1 × 0 = 0 and 0 × 0 = 0). This operation exists in all modern programming languages, for example in language C++ and Java it is marked as &.
In the first test case, the answer is calculated as summation of 6 subarrays as follow:
#include<iostream>
#include<stdio.h>
#include<bitset>
#include<cmath>
using namespace std;
const int maxn=1e5+5;
bitset<31>a[maxn];
int main()
{
int T;
while(scanf("%d",&T)!=EOF)
{
while(T--)
{
int n,temp;
int set=0;
scanf("%d",&n);
for(int i=0;i<n;i++)
{
scanf("%d",&temp);
set=max(set,(int)log2(temp)+1);
a[i]=bitset<31>(temp);
}
long long ans=0;
a[n]=bitset<31>(0);
for(int i=0;i<set;i++)
{
long long rco=0;
int flag=0;
// cout<<"+++++++=flag="<<flag<<endl;
for(int j=0;j<n+1;j++)
{
if(flag==0)
{
if(a[j][i]==1)
{
rco++;
flag=1;
}
}
else
{
if(a[j][i]==1)
{
rco++;
}
else
{
flag=0;
ans+=(1<<i)*(long long)rco*(rco+1)/2;
rco=0;
}
}
// cout<<"j="<<j<<" "<<"flag="<<flag<<" "<<rco<<" "<<ans<<endl;
}
// cout<<"--------------------"<<endl;
}
cout<<ans<<endl;
}
}
} 




 本文介绍了一道算法题目,要求计算给定整数数组的所有子区间中元素按位与运算结果之和的方法。通过分析与运算特性,采用二进制位处理技巧,实现了高效的求解算法。
本文介绍了一道算法题目,要求计算给定整数数组的所有子区间中元素按位与运算结果之和的方法。通过分析与运算特性,采用二进制位处理技巧,实现了高效的求解算法。
















 1665
1665

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








