本文探讨了图像退化的原因及处理方法，包括线性位移不变的图像退化模型，噪声模型如高斯、瑞丽、伽马、指数、均匀、脉冲噪声，以及周期噪声。介绍了空间滤波复原技术，如均值、中值、自适应中值滤波器，和频域滤波消减周期噪声的方法。同时，讨论了点扩散函数的估计、逆滤波和维纳滤波在图像复原中的应用。
虽然写这个博客主要目的是为了给我自己做一个思路记忆录，但是如果你恰好点了进来，那么先对你说一声欢迎。我并不是什么大触，只是一个菜菜的学生，如果您发现了什么错误或者您对于某些地方有更好的意见，非常欢迎您的斧正！
目录
①图像退化/复原过程的模型
√什么是图像退化？
图像的质量变坏叫做退化。退化的形式有图像模糊、图像有干扰等
√图像退化的原因
无论是由光学、光电或电子方法获得的图像都会有不同程度的退化；退化的形式多种多样。如传感器噪声、摄像机未聚焦、物体与摄像设备之间的相对移动、随机大气湍流、光学系统的相差、成像光源或射线的散射等；
√图像退化的处理方法
·如果我们对退化的类型、机制和过程都十分清楚，那么就可以利用其反过程来复原图像。
·典型的图像复原方法是根据图像退化的先验知识建立一个退化模型，以此模型为基础，采用滤波等手段进行处理，使得复原后的图像符合一定的准则，达到改善图像质量的目的。
图像复原
·与图像增强相似，图像复原的目的也是改善图像质量。
·图像增强主要是一个主观过程，而图像复原是一个客观过程。
·图像增强被认为是一种对比度拉伸，提供给用户喜欢接收的图像；而图像复原技术追求灰度原始图像的最优估值。
·图像复原技术可以使用空间域或频域滤波器实现。
·图像复原可以看做是图像退化的逆过程，是将图像退化的过程加以估计，建立退化的数学模型后，补偿退化过程造成的失真。
1、线性位移不变的图像退化模型
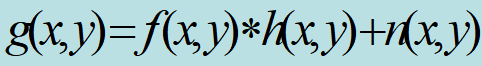
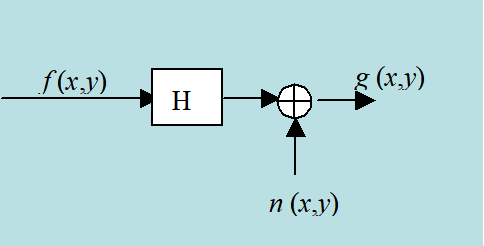
·f(x,y)表示一幅输入图像
·g(x,y)是f(x,y)产生的一幅退化图像
·H表示退化函数
·n(x,y)表示外加噪声
②噪声模型
2 .1噪声模型
√数字图像的噪声主要来源于图像的获取和传输过程
·图像获取的数字化过程，如图像传感器的质量和环境条件。
·图像传输过程中传输信道的噪声干扰，如通过无线网络传输的图像会受到光或其它大气因素的干扰。
√一些重要的噪声的概率密度函数（PDF）
√高斯噪声
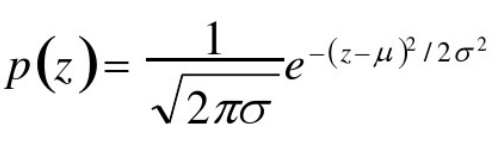
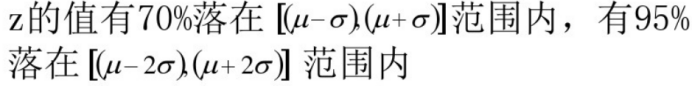
√瑞丽噪声
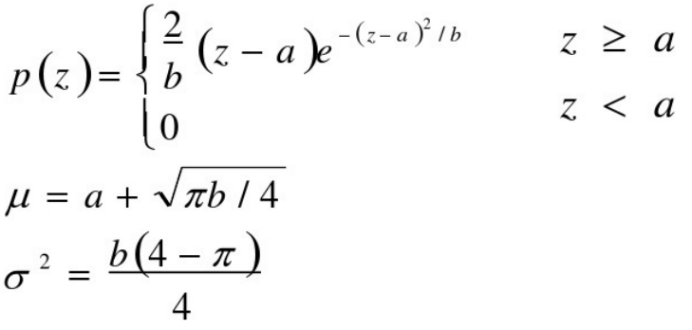
·距离原点的位移是a
·函数曲线向右变形
√伽马（爱尔兰）噪声
√指数噪声
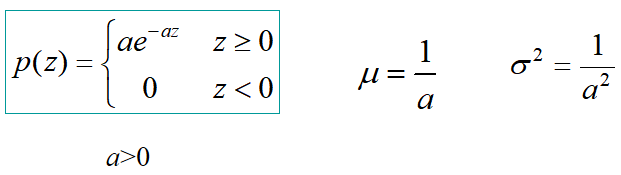
·指数分布的PDF是当b=1时爱尔兰分布的特殊情况。
√均匀噪声
√脉冲（椒盐）噪声
·如果Pa或Pb为0，则脉冲噪声称为单极脉冲。
·如果Pa或Pb均不为0，则脉冲噪声称为双极脉冲噪声或椒盐噪声。
·脉冲噪声可以为正，也可以为负
·标定以后，脉冲噪声总是数字化为最大值（纯黑或纯白）
·通常，负脉冲以黑点（胡椒点）出现，正脉冲以白点（盐点）出现。
√几种噪声的运用
·高斯噪声源于电子电路噪声和由低照明度或高温带来的传感器噪声
·瑞利噪声对分布在图像范围内特征化噪声有用
·伽马分布和指数分布用于激光成像噪声
·均匀密度分布作为模拟随机数产生器的基础
·脉冲噪声用于成像中的短暂停留中，如错误的开关操作。
√周期噪声
·周期噪声是在图像获取中从电力或极电干扰中产生。
·周期噪声可以通过频率域滤波显著减少。
2.2空间滤波复原
均值滤波器 | ||
| 算术均值滤波器 |
| ·Sxy表示中心在(x,y)，尺寸为m×n的矩形窗口 ·平滑了一幅图像的局部变化 ·在模糊了结果的同时减少了噪声 |
| 几何均值滤波器 |
| ·几何均值滤波器所达到的平滑度可以与算数均值滤波器相比 ·但几何均值滤波器在滤波过程中，与算数均值滤波器相比，会丢失更少的图像细节——相对锐化 |
| 谐波均值滤波器 |
| ·谐波均值滤波器对于“盐”噪声效果好，但不适用与“胡椒”噪声 ·善于处理高斯噪声等 |
| ·算数均值滤波器和几何均值滤波器适合于处理高斯或均匀等随机噪声 ·谐波均值滤波器适合于处理脉冲噪声。 | ||
|
| ||
顺序统计滤波器 | ||
| 中值滤波器 |
| ·在相同尺寸下，比起均值滤波器引起的模糊少。 ·对单极或双极脉冲噪声非常有效 |
| 最大值滤波器 |
| ·用于发现图像中的最亮点 ·可以有效过滤“胡椒”噪声（因为“胡椒”噪声是非常低的值） |
| 最小值滤波器 |
| ·用于发现图像中的最暗点 ·可以有效过滤“盐”噪声（因为“盐”噪声是非常高的值） |
| 中点滤波器 |
| ·结合了顺序统计和求平均 ·对于高斯和均匀随机分布这类噪声有最好的效果 |
|
| ||
自适应中值滤波器 | ||
| 目的： ·除去“椒盐”噪声（冲激噪声） ·平滑其它非冲激噪声 ·减少物体边界细化或粗化等失真 | ||
|
| ||
2.3频域滤波消减周期噪声
·周期噪声是在图像获取过程中从电力或机电干扰中产生的。
·这是唯一的一种空间依赖型噪声
·可以通过专用的带阻、带通和陷波滤波器来削减或消除周期性噪声干扰。
√带阻滤波器
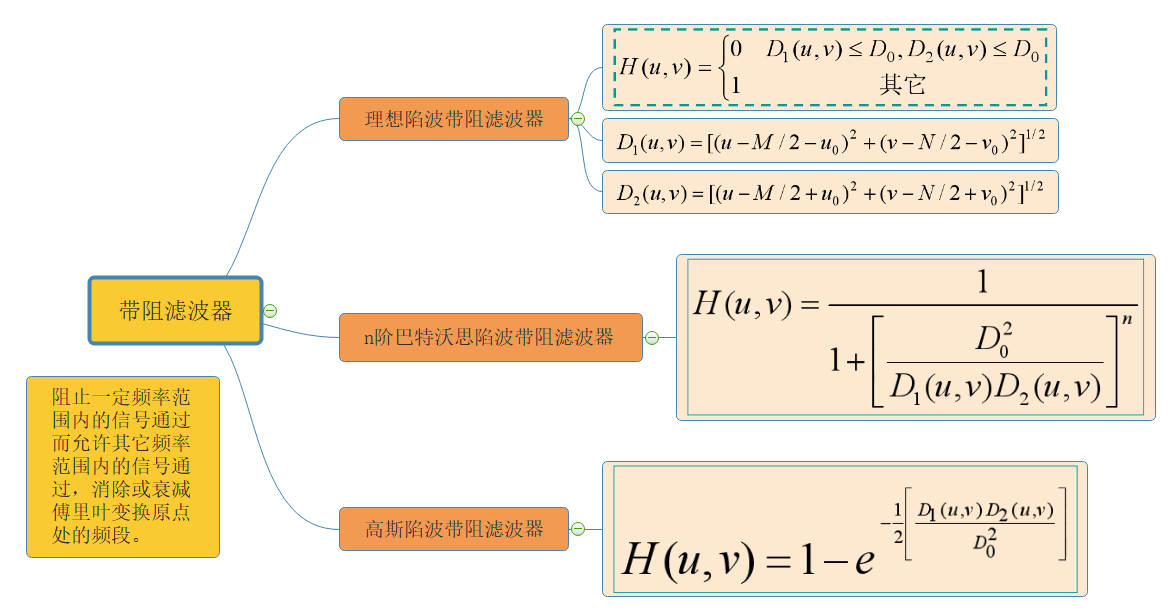
√带阻滤波器的透视图
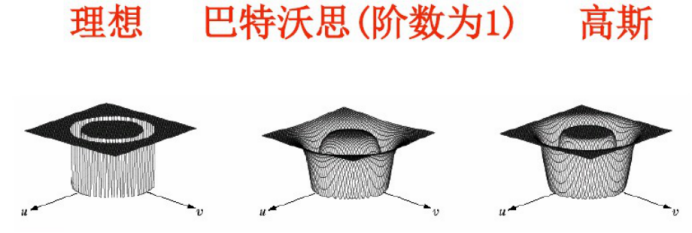
√应用举例
√陷波滤波器
·阻止或通过事先定义的中心频率邻域内的频率
·由于傅里叶变换是对称的，陷波滤波器必须以关于原点对称的形式出现
·如果陷波滤波器位于原点处，则以它本身形式出现
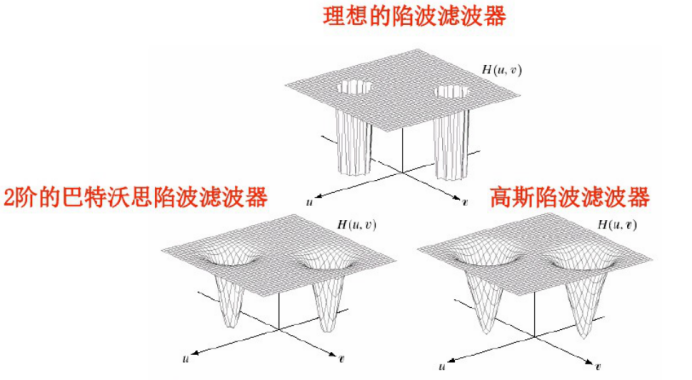
√陷波滤波器消除周期噪声的实例
③点扩散函数的估计
1、图像观察估计法
·根据已知的退化图像，收集图像自身的信息。可以通过选取图像中的包含简单结构或强信号区的子图来估计，从而找到退化模型H。
2、试验估计法
·通过系统装置得到与退化图像相似的图像，从而获得退化模型。
·具体做法：通过系统装置，成像一个脉冲（小亮点），得到其退化的冲激相应。该冲激的傅里叶变换是一个常数，则：
3、模型估计法
·通过分析退化原因，根据退化原理运用数学手断推导出退化模型。例如①匀速直线运动造成的模糊，即可通过该方法推导而得；②基于大气湍流的物理特性而得到的退化模型：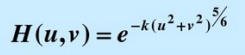
k是一个与湍流性质相关的函数
④逆滤波
·对于图像退化模型
两边取傅立叶变换
H(u,v)又称为系统的转移函数(或滤波函数)，它使图像退化。
在无噪声的情况下，上式可以简化为：
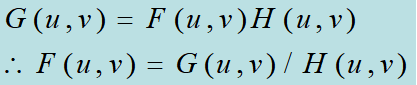
这种1/H(u,v)的形式称为逆滤波。再进行傅立叶逆变换就可以得到f(x,y)。
这种1/H(u,v)的形式称为逆滤波。再进行傅立叶逆变换就可以得到f(x,y)。
·实验证明，当退化图像的噪声较小，即轻度降质时，采用逆滤波恢复的方法可以获得较好的结果。
·当噪声作用范围很大时，逆滤波不能从噪声中提取图像。
·逆滤波恢复方法对噪声极为敏感，要求信噪比较高，通常不满足该条件。
·为了解决高噪声情况下的图像恢复问题，可采用最小均方滤波器来解决，其中，用得最多的是维纳滤波器。
·逆滤波实例：
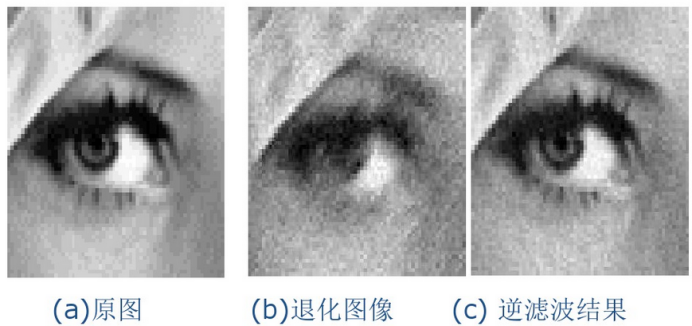
⑤维纳滤波
√维纳滤波器的传递函数
√特点
·自动抑制噪声 
不会被0除
·逆滤波是维纳滤波的特例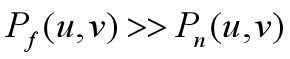 
·猛烈湍流退化退图像；逆滤波；频率受限逆滤波；纳维斯滤波复原
扫一扫
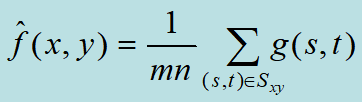
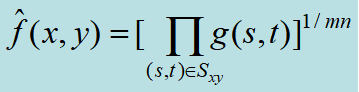
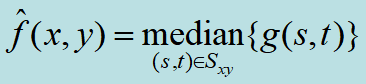
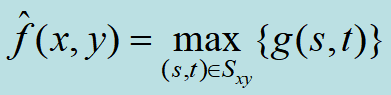
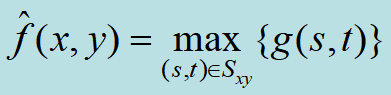
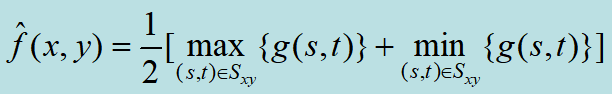
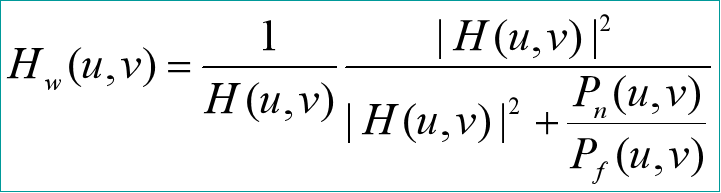
1679
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
