算法（1）

一、数组循环移位算法

设计一个算法，把一个含有 N 个元素的数组循环右移 K 位，要求时间复杂度为

O（N），且只允许使用两个附加变量。

（1）问题：什么时数组循环移位呢？

比如，A={1，2，3，4}循环右移1位，结果为，4，1，2，3

A循环右移两位结果为，3，4，1，2

（2）如何实现？

如果移动1位，我们容易想到，将最后一个元素先存起来，然后将其余元素后移一位，再将之前存起来的元素放入第一个位置

移动两位，将倒数第1个存起来，其余元素移动两位，再将之前存起来的元素放入第一个位置

      （下面都是从初始状态进行的移动）

初始	1	2	3	4
m1	4	1	2	3
m2	3	4	1	2
m3	2	3	4	1
m4	1	2	3	4

void rightShift(int* arr, int n, int k)
{	int i;
	while(k--)
	{
	int t = arr[n-1];
	for( i = n-1; i > 0; i--)
	arr[i] = arr[i-1];
	arr[0] = t;	 
	 }
}

右移k位，比如要移动2位，先移动一位一次，然后在移动一位一次。（k--的作用）

（3）如何达到题目要求
上面的解法比较简单，但是达不到题目的复杂度要求。

比如 12345abcde，向右移 4 个位置后变为 bcde12345a, bcde 和 12345a 顺序都不

变，仔细观察后，可以这样处理：

(1)12345a 反转得 a54321；

(2) bcde 反转得 edcb，此时数组 a54321edcb；

(3) 再反转 bcde12345a；复杂度 O(N)。

关键：逆序代码，比如A={1，2，3，4}，5对应数组下标为0，1，2，3

设temp,temp=A[0]=1,A[0]=A[3]=4,A[3]=temp=1    结果为  4，2，3，1

             temp=A[1]=2,A[1]=A[2]=3,A[3]=temp=2    结果为  4，3，2，1

#include<stdio.h>
void reverse(int*arr,int begin,int end)
{
for( ; begin<end; begin++, end--) //实现逆序
{
	int temp=arr[begin];
	arr[begin]=arr[end];
	arr[end]=temp;
}
}
void rightShift1(int* arr,int k,int n)
{
k%=n;
reverse(arr,0,n-k-1);
reverse(arr,n-k,n-1);
reverse(arr,0,n-1);
}

void rightShift2(int* arr, int n, int k)
{	int i;
	while(k--)
	{
	int t = arr[n-1];
	for( i = n-1; i > 0; i--)
	arr[i] = arr[i-1];
	arr[0] = t;
	 
	 }
}
void Print(int arr[],int n){
	int i;
	for(i=0;i<n;i++){
	printf("%d ",arr[i]);	
	}	
}
int main()
{ 	int A[]={1,2,3,4};
	int B[]={1,2,3,4,5,6,7,8,9,10}; 
 	int l1=sizeof(A)/sizeof(A[0]);
 	int l2=sizeof(B)/sizeof(B[0]);
	rightShift2(A,l1,1);
	printf("方法1:\n");
	Print(A,l1);
	printf("\n");
	rightShift2(B,l2,5);
	printf("方法2:\n");
	Print(B,l2);	
 	return 0;
}

二、实现矩阵转置

（1）问题分析

矩阵转置，把矩阵的行环成同序数的列得到新矩阵，如下图对角线

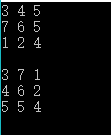
观察可得，(aij代表位置)即为a12与与a21互换，a13与与a31互换，a23与a32互换

实质为交换：设temp,temp=A[i][j], A[i][j]=A[j][i],A[j][i]=temp

（2）实现

此处设立一个数组来存储转置矩  ↵

示例：

i=0,

j=0 ,  temp[0] [0]=arr[0][0] ,

j=1, temp[0] [1]=arr1][0] ,

j=2, temp[0] [2]=arr[2][0] ,

#include<stdio.h>
#define row 3
#define col 3
void Tran(int arr[row][col]){
	int i,j,temp[row][col];
	for(i=0;i<col;i++){
		for(j=0;j<row;j++)
			temp[i][j]=arr[j][i];
	}
	//打印转置后的数组 
	for(i=0;i<row;i++){
		for(j=0;j<col;j++){
			printf("%d ",temp[i][j]);
			}
		printf("\n");	
		}		
}
int main(void){
	int arr[row][col]={{3,4,5},{7,6,5},{1,2,4}};
	Tran(arr);
}

三、完数

编程实现给出指定整数范围  【a,b】内的所有完数，一个数恰好等于除它本身外的所有因子和，此数称为完数，例如6=1+2+3

（1）分析

因子和，则需求出因子，6%1=0,6%2=0，6%3=0，6%4!=0,6%5!=0,因子和1+2+3=6

一层循环指定遍历区间

二层循环求因子和，1为任何数的因子，从2开始到指定范围

if语句判断是否为完数

（2）实现

#include<stdio.h>
void FindWS(int begin,int end){
	int i,j,temp;
	for(i=begin+1;i<end;++i)
	{	temp=1;
		for(j=2;j<i;++j){
		if(i%j==0){
			temp=temp+j;
			}
		}
		if(temp==i){
		printf("%d\n",i);
		}
	}
}
int main(void){
	FindWS(2,30);	 
}

四、压缩字符串

对于字符串中连续出现的同一字符，用该字符加上连续出现的次数来表示（连续出现次数小于3的不压缩）

   设计程序将采用该压缩方法后的字符串解压还原为原  字符串并输出

注意字母后方跟的数字不一定是一位的 

连续出现 2 次直接写即可（题目说连续出现次数小于 3 不压缩）

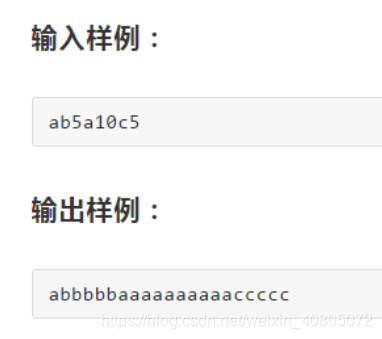
第一个a出现一次，输出一个a;b后面为5，输出5个5;a后面为10输出10个a;c后面为5，输出5个c

#include<stdio.h>

int main(void){
	int i=0,sum,count,k;
	char s[100];
	gets(s);
	while(s[i]){
		printf("%c",s[i]);
		i++;
		sum=0;
		count=0;
		while(s[i]>='0'&&s[i]<='9'){
			sum=sum*10+s[i]-'0';
			i++;
			count++;
		}
		for(k=0;k<sum-1;k++){
			printf("%c",s[i-count-1]);
		}
	}	 
}