统计学习方法笔记（一）

1. 统计学习方法三要素：模型，策略，算法
2. 统计学习方法步骤;(a)得到一个有限训练集（b）确定所有的可能模型（学习模型的集合）（c）确定学习的策略（即模型选择的准则）（d）学习最优模型的算法（e）最优模型对新数据的预测和分析。
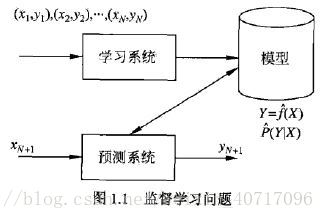
3. 监督学习：利用训练数据集学习一个模型，再用模型对测试样本进行预测。（训练数据集往往是人工给出）
4. 损失函数：度量预测错误的程度。损失函数是f(x)和Y的非负实值函数，记作L(Y,f(X)).
   
   损失函数值越小，模型就越好。
5. 风险函数（期望损失）：有图模型的输入，输出（X,Y）是随机变量，遵循联合分布，所以损失函数的期望是
   

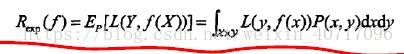
6.模型f(X)关于训练数据集的平均损失称为经验损失或者经验风险：

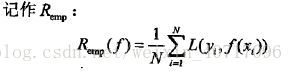
7. 期望风险Rexp(f)是模型关于联合分布的期望损失；经验风险Remp(f)是模型关于训练样本集的平均损失。
8. 大数据定律：当样本容量N趋于无穷是，经验风险趋于期望风险。
9. 利用经验风险估计期望风险（由于样本数目有限，所以用经验风险估计期望风险并不理想）
10. 对经验风险进行一定程度矫正，采用两个策略*（经验风险最小化和结构风险最小化）*
11. 经验风险最小化（ERM）策略认为，经验风险最小的模型就是最优模型。（转化求解最优化问题）

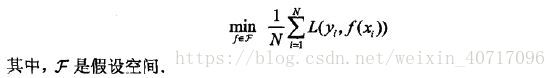
12.极大似然估计就是经验风险最小化的例子。（当模型是条件概率分布，损失函数是对数函数时，经验风险最小化就等于极大似然估计。）；但是当样本过小时，会出现“过拟合现象”。
13. 结构风险最小化：是为了防止过拟合而提出的策略。结构风险最小化等于正则化。增加一项正则化或者罚项。

14. 结构风险需要经验风险和模型复杂度同时小。结构风险小的模型往往对训练数据以及未知预测数据都有较好的预测。
15. 将学习方法对未知数据的预测能力称为泛化能力（后补充）。
16. 过拟合：一味追求提高对训练数据的预测能力，所选的模型的复杂度往往会比真模型更高，这种现象称为过拟合（over-fitting）。对已知数据预测的很好，但是对未知数据预测很差的现象。
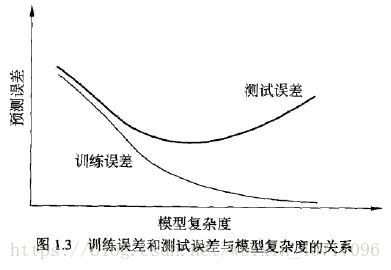
17. 随着模型复杂度的增加，训练误差会减小，直至趋于0；但是测试误差却不会如此；测试误差会随着模型复杂度的增加先减小而后增大。但是最终的目的是使测试误差达到最小。因此要选择合适的多项式次数，以达到这一目的。