解决回文串问题的两种模板解法

我们可以发现leetcode中有很多回文相关的问题，是常考点。这些题目大多是求回文子串长度或输出所有回文字串又或是分割回文串等，而大部分和回文串相关的问题都可以由两种模板方法解决。
以最经典的leetcode第五题为例子：

模板方法一：动态规划

我们定义dp[i][j]表示字符串i～j是否是回文子串，那么我们可以得出状态转移方程

if(dp[i+1][j-1] == 1 && s[i] == s[j])
	dp[i][j] = 1

完整代码：

class Solution {
public:
    string longestPalindrome(string& s) {
        string res = "";
        vector<vector<int>> dp(s.size(),vector<int>(s.size(),0));
        for(int len=0;len<s.size();len++){
            for(int index=0;index+len<s.size();index++){
                int i=index;
                int j=index+len;
                if(len == 0)
                    dp[i][j] = 1;
                else if(len == 1){
                    if(s[i] == s[j])
                        dp[i][j] = 1;
                }
                else{
                    if(dp[i+1][j-1] == 1 && s[i] == s[j])
                        dp[i][j] = 1;
                }
                if(dp[i][j] == 1 && (len+1)>res.size())
                    res = s.substr(i,len+1);
            }
        }
        
        return res;

    }
};

这种方法的效率比较低

模板方法二：中心扩展法

我们可以枚举出所有可能的子串，然后对每个子串来判断是否是回文串，但是这样做就太搓了。
下面的解释来自官方题解析：https://leetcode-cn.com/problems/palindromic-substrings/solution/hui-wen-zi-chuan-by-leetcode-solution/
我们可以：枚举每一个可能的回文中心，然后用两个指针分别向左右两边拓展，当两个指针指向的元素相同的时候就拓展，否则停止拓展。
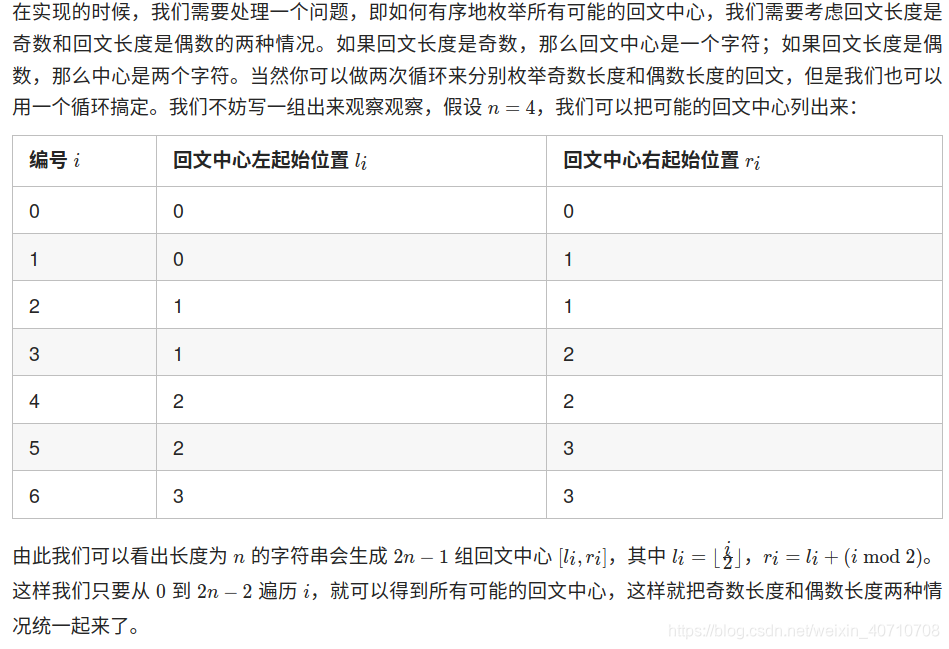代码：

class Solution {
public:
    string longestPalindrome(string s) {
        int len = s.size();
        string res = "";
        for(int i = 0;i<2*len-1;i++){
            int l = i/2;
            int r = l+(i%2);
            while(l>=0 && r<len && s[l]==s[r]){
                if(r-l+1>res.size())
                    res = s.substr(l,r-l+1);
                l--;
                r++;
            }
        }
        return res;
    }
};