牛客网错题记录（不断更新中~

最新推荐文章于 2025-06-09 09:32:51 发布

原创最新推荐文章于 2025-06-09 09:32:51 发布 · 483 阅读

1 ·

CC 4.0 BY-SA版权

文章标签：

#笔试题

js 同时被 2 个专栏收录

12 篇文章

订阅专栏

html/css

8 篇文章

订阅专栏

本文探讨了前端开发中常见的陷阱及解决方法，包括Boolean类型的误判、浮动元素的行为、构造函数的返回值、事件监听的阶段等问题，并提供了优化建议。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

1.一个值为false的Boolean对象被if强制转换时为true

        var x = new Boolean(false);//x为Boolean引用类型
        var y = Boolean(false);//y为Boolean原始类型        
        console.log(x);//Boolean {false}
        console.log(y);//false

此时用if(x)进行判断，会将x判断为true

2.当一个行内元素浮动的时候相当于设置display：inline-block

<div style=”width:400px;height:200px;”>
  <span style=”float:left;width:auto;height:100%;”>
           <i style=”position:absolute;float:left;width:100px;height:50px;”>hello</i>
  </span>
</div>

问题：span标签的width和height分别为多少？

首先，span作为一个行内元素本来是没法设宽高的，但是因为有float:left所以它被变为一个行内块级元素，高度为父亲高度的100%，宽为auto也就是随着内部元素的大小走；其次，内部position:absolute脱离文本流所以没有宽。所以span的width为0，height为200px。

在这里我犯了一个错误虽然不影响结果，但是问题本身错的非常离谱。后经查证，浮动的块虽然脱离的正常的文档流，但是没有脱离文本流。而position:absolute既脱离文档流也脱离文本流，是绝对脱离。虽然二者都会带来高度塌陷，但float没有宽度塌陷（父元素宽随float的子元素），而position:absolute还有宽度塌陷（父元素宽为0），这些塌陷都是对父元素有影响，并不会改变自己的宽。

出个脑筋急转弯：

    <div style="width:400px;height:200px;">
        <div style="width:auto;height:100%;">
            <i style="float:left;width:100px;height:50px;">hello</i>
        </div>
    </div>

这时候里面的div应该是多宽多高呢？应该是宽400px，高200px因为div是块级元素听他爹的。

<div style="width:400px;height:200px;">
   <div style="width:auto;height:100%;display:inline-block;">
       <i style="float:left;width:100px;height:50px;">hello</i>
   </div>
</div>

加了行内块级才能让他听孩子决定宽（因为宽是auto）！如果高是auto，高也由儿子决定。但现在高是100%，所以由父亲决定。

我们整理一下上面的内容：

inline-block默认auto，让子元素进行决定；一旦改为100%，则由父元素进行决定。
float不会造成父元素宽度塌陷，absolute会造成父元素宽度塌陷。

提到float不由得让我想起去头条面试时的一道基础题……非常基础……但我答得非常差劲

两列布局(左固定右自适应)

①使用float+margin

        #div1 {
            border: 2px dashed red;
            width: 200px;
            float: left;
        }
        #div2 {
            border: 5px solid deepskyblue;
            margin-left: 204px;
        }

此方法还可使用absolute+margin-left方法，异曲同工之妙。

②使用float+overflow:hidden

        #div1 {
            border: 2px dashed red;
            width: 200px;
            float: left;
        }
        #div2 {
            border: 5px solid deepskyblue;
            overflow: auto;//或者hidden
        }

③使用inline-block以及cal()

        #div1 {
            border: 2px dashed red;
            width: 200px;
            display: inline-block;
        }
        #div2 {
            border: 5px solid deepskyblue;
            display: inline-block;
            width:calc(100% - 204px);   
            box-sizing: border-box; //很重要，否则div2会下去，因为默认是content-box     
        }

注意去除inline-block元素之间的空隙：letter-spacing（字符间距）、word-spacing（单词间距）、font-size:0等。

④父元素使用flex

        body {
            display: flex;
        }
        #div1 {
            border: 2px dashed red;
            width: 200px;
        }
        #div2 {
            border: 5px solid deepskyblue;
            flex: 1;
        }

3.var test='4399'-0;

js解释器会将字符串‘4399’调用Number()转成4399再去计算。

4.搞明白虽然数组是个对象，但给他的属性都和length是并列的。

答案是：2，因为对象不能用length返回其拥有的属性数量。

5.img标签的onerror事件

当img中的src图片加载失败（或是根本没有），则触发onerror事件。

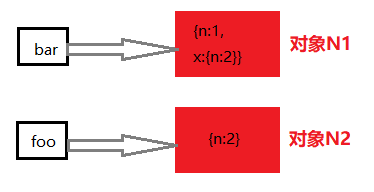
6.连续赋值与求值顺序

var foo = {n:1};
var bar = foo;
foo.x = foo = {n:2}

这道题考察的知识点是计算顺序：从左到右将每个引用替换为真实的对象的属性，从右到左将值赋给每个引用；以及运算符的优先级，**.**点的运算优先级是最高的。

具体的过程是这样的：

①foo指向对象N1，这个N1里面的内容是{n:1}

②bar指向对象N1，这个N1里面的内容是{n:1}

③因为点的运算优先级高所以我们会先“计算”foo.x，也就是给N1里面加了一个x属性，但是没有给值，于是N1里的内容为：{ n:1, x:undefined }

④计算顺序是从右到左赋值，所以第一个赋值是改变foo指向，foo指向一个新的对象N2，N2里面的内容是{n:2}

⑤终于到了给我们的foo.x赋值了，这个时候由于已经将foo.x解析过了，其实相当于给N1这个具体的对象赋值，此时N1：{n:1, x:{ n:2 } }

如下图所示：

7.构造函数返回了个啥

使用new为构造函数创建实例的时候，会隐含返回一个this，也就是构造函数创造的Object，如果我们自行添加一个返回，它会看你返回的是不是个对象，如果是个对象就用你返回的了。

        var xuuu = 123;
        function  test() {
            var xuuu = 456;
            this.aa = 6666;     
            return function() {
                console.log(xuuu);
                console.log(this.aa);
                console.log(this.xuuu); 
            };
        };
        var sdf = new test();
        console.log(sdf);//f()
        console.log(sdf.aa);//undefined
        sdf();//456 undefined 123

8.forEach和map

个人感觉forEach能做的事情，map都可以干，所以还是用map保险点。而且forEach和map对原数组作出更改，如果我们想获取新数组只能用map，因为map返回新数组，而forEach没有返回值。

而且map最后一定是return 这个新的ele，形如：

var arr = ["1","2","3"];
arr = arr.map(ele=>{
    return +ele;
});

牛客网上的数据都是字符串所以需要这一步进行转换成number型。

9.事件三个阶段

<div id="div2">

    <div id="div1">点我</div>

</div>

var div2=document.getElementById('div2');

var div1=document.getElementById('div1');

 

div1.addEventListener('click', function(event){console.log("A");}, true);

div2.addEventListener('click', function(event){console.log("B");});

div1.addEventListener('click', function(event){console.log("C");}, false);

div2.addEventListener('click', function(event){console.log("D");}, true);

事件三阶段包括：

捕获阶段
目标阶段
冒泡阶段

addEventListener的第三个参数表示是否会在事件捕获阶段进行触发，默认为false，所以正确顺序为：DACB

10.arguments只是类数组

arguments不是真正的数组，因为它有自己的属性，它只是像数组一样有length，但不可以使用数组的方法去操作它。

arguments转化成数组通过Array.prototype.slice.apply(null,arguments)

11.addEventListener异步调用的i值

是阿里的一道题，此题目前没有标答，题目描述如下：
下面HTML中的内嵌JS代码会生成一个列表，格式为"{index}. {点击目标的全名}"。于此同时当点击列表中的某个名字会在控制台中输出"click on no.{点击目标的index} {firstName},{lastName}"。请尝试指出代码中存在的BUG以及可能会发生的性能问题，并从优雅、高效、可读性以及性能方面进行优化，在指出问题的同时请尽量给出修正代码。

<meta charset="UTF-8">
<title>Title</title>
  
  
<ul id="list">
  
</ul>
  
<script>
  maxLength = 4;
  list = document.querySelector('#list');
  
  function processName(name) {
    return {
      firstName: name[0],
      lastName: name[1],
      getFullName() {
        return this.firstName + ' ' + this.lastName;
      },
    };
  }
  
  var names = [
    ['Gregor', 'Bachmann'],
    ['Anita', 'Bruns'],
    ['Anke', 'Dorn'],
    ['Ulrich', 'Koch'],
    ['Dietrich', 'Riedl'],
    ['Wolfgang', 'Jahn'],
    ['Gesine', 'Sturm'],
    ['Theodor', 'Petersen'],
  ];
  
  var validCount = 0;
for (var i = 0; i < names.length; i += 1) {
    var flag1 = names[i][0].indexOf('A') !== 0;
    var getFullName;
    if (flag1 && names[i][0].length >= 4) {
      getFullName = processName(names[i]).getFullName;
      var lastName = processName(names[i]).lastName;
      var firstName = processName(names[i]).firstName;
      var span = document.createElement('li');
      var textNode = document.createTextNode(i + 1 + '. ' + getFullName());
      span.appendChild(textNode);
      span.addEventListener('click', function () {
        console.log('click on no.' + i + ' ' + firstName + ',' + lastName);
      });
      if (validCount + 1 > maxLength) {
        continue;
      }
      validCount += 1;
      list.appendChild(span);
    }
  }
</script>

我的更改是：

var validCount = 0;
 
var docFrag = document.createDocumentFragment();//文档碎片，减少回流和重绘
 
for (var i = 0; i names.length; i += 1) {
 
    var flag1 = names[i][0].indexOf('A') !== 0;//第一位不是A的
 
    var getFullName;
 
    if (flag1 && names[i][0].length > 4) {
 
      getFullName = processName(names[i]).getFullName;
 
      var lastName = processName(names[i]).lastName;
 
      var firstName = processName(names[i]).firstName;
 
      var span = document.createElement('li');
 
      var textNode = document.createTextNode(i + 1 + '. ' + getFullName());
 
      span.appendChild(textNode);
 
      span.index = i;
 
      span.first = firstName;
 
      span.last = lastName;
 
      span.addEventListener('click', function (ev) {
 
        console.log('click on no.' + (ev.target.index+1) + ' ' + ev.target.first + ',' + ev.target.last);
 
      });
 
      if (validCount + 1 > maxLength) {
 
        break;//直接跳出循环
 
      }
 
      validCount += 1;
 
      docFrag.appendChild(span);
 
    }
 
  }
 
list.appendChild(docFrag);

我觉得问题主要出在addEventListener是异步的，读的i肯定是循环完毕的i值，而不是每一次的i值，firstName和lastName也是同理。还有性能优化方面可以避免多次的回流重绘，可以使用文档碎片；以及跳出循环使用break就不要使用continue了，因为continue是只跳出这一次而break是停止整个循环。差不多我就想到这么几个。希望大家帮我多多指出不足~