关键路径法是进度网络分析技术的一种。
它在不考虑任何资源限制的情况下,沿着进度网络:
-
先使用顺推的方法计算出所有活动的最早开始、最早结束时间。
-
再使用逆推的方法计算出所有活动的最晚开始、最晚结束时间。
-
随后用两者的差值计算出每个活动可以推迟或拖延的浮动时间。
以此在进度模型中:
-
估算项目的最短工期;
-
并确定逻辑网络路径的总浮动时间(进度灵活性)。
-
同时,找出项目的关键路径(“总浮动时间=0的路径);
关键路径之所以重要,是因为在该路径上的任意一个活动的推迟完成都会拖延整个项目的进度;同理,其上任意一个活动的提前完成也会加速整个项目的进度。
因此,项目经理应该重点关注在关键路径上的所有活动。
下文将借用《PMBOK指南》第六版中的一个例子做详细说明。
在一个项目中,一共有A,B,C,D四个活动,已知:
-
活动A的持续时间为5天;
-
活动B的持续时间为5天,活动C的持续时间为10天,且活动B和C在活动A完成后才能开始;
-
活动D的持续时间为15天,且只有在活动B和C都完成后才能开始;
-
活动D完成后,整个项目才算完成。
第一步:绘制活动进度网络图,并填入持续时间
-
根据活动之间的逻辑关系,绘制活动进度网络图;
-
并在每个活动的“持续时间”格内填入该活动的持续时间。
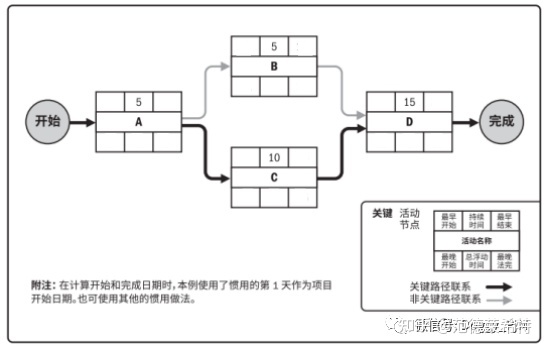
(图中“最晚法完”应为“最晚结束”)
第二步:“顺推”出所有活动的最早开始、最早结束时间
在“顺推”中假设每个活动都能根据逻辑顺序尽可能早的开始,以此来估算完成项目所需的最短工期。
-
“顺推”的几个规则
-
在初始活动的“最早开始”格内填入时间“1”,也就是第一天。
-
根据“持续时间”格内的数据推算出“最早结束”格内的时间。
“最早结束” = “最早开始” + “持续时间” - 1 -
下一活动的“最早开始”时间是所有前置活动的“最早结束”时间中的最大值之后一天。
下一活动“最早开始” = max{前置活动“最早结束”} + 1
这是因为,所有活动都是根据逻辑顺序尽可能早的开始,-
当某个活动只有一个前置活动时,其都在前置活动结束后一天开始。
-
当遇见某个活动有多个前置活动的时候,其在最后结束的前置活动之后一天开始
-
-
根据上述描述的顺推规则,填写每个活动的“最早开始”和“最早结束”时间。
-
最后一个活动的“最早结束”时间也就是项目的最短工期。
最短工期 = 最后一个活动“最早结束”
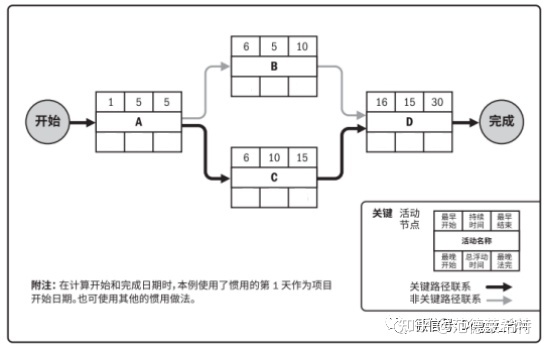
(图中“最晚法完”应为“最晚结束”)
第三步:“逆推”出所有活动的最晚开始、最晚结束时间
在“逆推”中假设每个活动都能根据逻辑顺序尽可能晚的结束,为之后研究每个活动的浮动时间打下基础。
-
“逆推”的几个规则
-
在项目“完成”的前置任务的“最晚结束”格内填入“最短工期”。
-
根据“持续时间”格内的数据推算出“最晚开始”格内的时间。
“最晚开始” = “最晚结束” + 1 - “持续时间” -
上一活动的“最晚结束”时间是所有后置活动的“最晚开始”时间中的最小值之前一天。
上一活动“最晚结束” = min{后活动“最晚开始”} - 1
这是因为,所有活动都是根据逻辑顺序尽可能晚的结束,-
当某个活动只有一个后置活动时,其都在后置活动开始前一天结束。
-
当遇见某个活动有多个后置活动的时候,其在最早开始的后置活动之前一天开始
-
-
根据上述描述的顺推规则,填写每个活动的“最晚结束”和“最晚开始”时间。
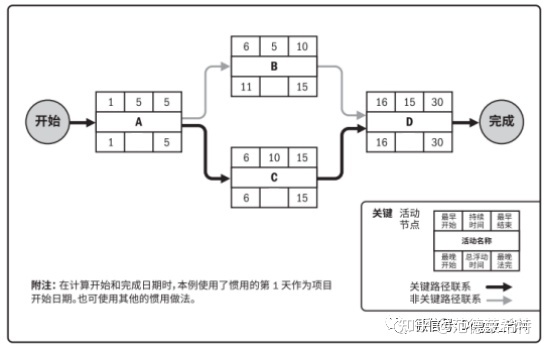
(图中“最晚法完”应为“最晚结束”)
第四步:根据“差值”确定所有活动的浮动时间
-
根据“顺推得出的最早活动时间”与“逆推得出的最晚活动时间”之间的差值,可以确定每个活动的“浮动时间”
“浮动时间” = “最晚开始” - “最早开始”,或者
“浮动时间” = “最晚结束” - “最早结束” -
“浮动时间”是指某活动在不延误任何后置活动的最早开始日期或不违反制约因素的前提下,其可以推迟的时间量。
-
当某一活动路径上的所有活动的“浮动时间”之和,即“总浮动时间”,为“0”的时候,该路径为“关键路径”。
-
关键路径是项目中时间最长的活动顺序,决定着可能的项目最短工期。

(图中“最晚法完”应为“最晚结束”)
当我们将用关键路径法绘制完成的活动进度网格图转化成甘特图,我们就能清晰的知道,在该项目中:
-
活动B可以有5天的浮动时间;
-
活动A,C,D没有任何活动时间,需要格外的关注。
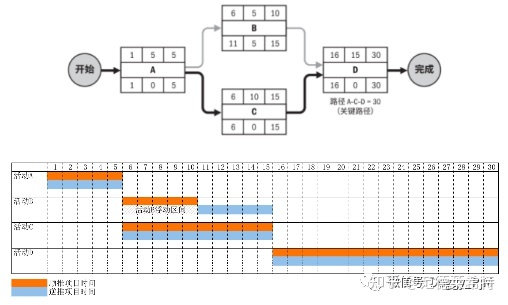
如此在做项目进度规划和进度监控的时候,或者到项目资源出现意料外的状况的时候,我们就可以知道哪些活动是可以放一放,哪些活动是一定要按时完成的。但是,“关键路径法”只是项目进度规划的工具之一,想要真正做好项目进度规划,一定要和其它工具配合使用。

























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








