39. Combination Sum 回溯算法简析_compounded sofr回溯2天怎么计算-优快云博客

本文介绍了一种使用回溯算法解决LeetCode上的组合求和问题的方法，通过深度优先遍历并设置适当的终止条件来寻找所有可能的解。文章还详细解释了如何避免重复解及无效遍历。

这道题要求给你一组正数 C，然后给你一个目标数 T，让你从那组C中找到加在一起等于 T 的那些组合。

例如：给你 [2，3，6，7] 和 7，则返回 [[2，2，3]，[7] ] 。

想解决这个问题前，我们首先引入一个新问题，图（树）的遍历问题。

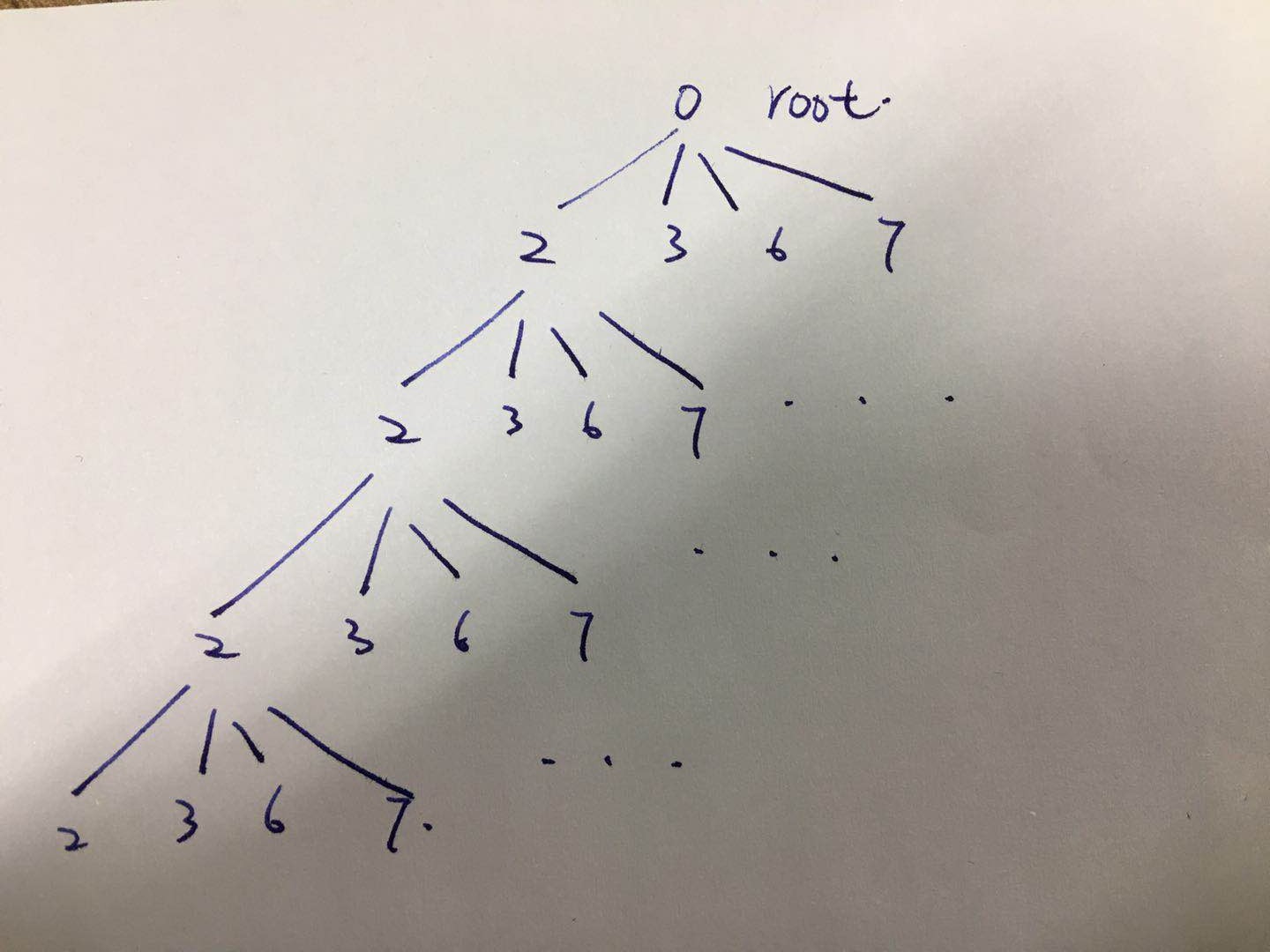
假如我们想要深度优先遍历这个树，返回[ [2,2,2,2] , [2,2,2,3] , [...] ... ]，我们需要从左边一直访问下去，进入第四层，得到[2, 2, 2, 2]，然后返回到第三层得到 [2, 2, 2 ]，再进入到第四层，得到 [2, 2, 2, 3] ... 得到[ 2, 2, 2, 7 ]之后，第三层的 “2” 及其子树就全部遍历完成，这时候就需要返回到第二层，得到[2，2]，进入第三层的 [2, 2, 3] ... 知道全部遍历完成。

即一个典型的回溯算法，对于回溯算法（探索与回溯法），是一种选优搜索法，又称为试探法，按选优条件向前搜索，以达到目标。但当探索到某一步时，发现原先选择并不优或达不到目标，就退回一步重新选择，这种走不通就退回再走的技术为回溯法，而满足回溯条件的某个状态的点称为“回溯点”。。

以深度遍历为例，当访问到第四层时，我们得到了一个正确结果，除了正确结果意外的点，都是“回溯点”。

代码实现：

class Solution(object):
    def SampleHuisu(self, candidates, temp, level, result):
        if level == 4: #正确结果
            result.append(temp[:])
        else:
            for i in candidates:
                if 1: #与之后比较使用
                    temp.append(i)
                    self.SampleHuisu(candidates, temp, level+1, result)
                    temp.pop()

result = []
A = Solution()
A.SampleHuisu([2, 3, 6, 7], [], 0, result)
print(result)

下面，我们来解决之前的问题，只需要在遍历问题上加一些条件：

1. 正确结果，应该是遍历得到的节点之和等于 target

2. 如果遍历得到的节点之和大于 target，则不需要继续向下遍历

3. 为了保证输出的结果没有重复，我们要求向下遍历时，节点的值必须是非递减的（假设），即不会访问 [2, 2, 3, 2] 或者 [2, 3, 2, ? ] 这样的节点。

代码如下：

class Solution(object):
    def huisu(self, candidates, temp, target, result):
        sum = 0
        for i in temp:
            sum += i
        if sum >= target:
            if sum == target:
                result.append(temp[:])
        else:
            for i in candidates:
                if temp == [] or i >= temp[-1]:
                    temp.append(i)
                    self.huisu(candidates, temp, target, result)
                    temp.pop()

    def combinationSum(self, candidates, target):
        result = []
        self.huisu(candidates, [], target, result)
        return result

result = []
A = Solution()
result = A.combinationSum([2, 3, 6, 7], 7)
print(result)

问题解决！