选择排序

• 算法思想
  首先选出最小（或最大）的一个数与第一个位置的数交换；在剩下的数当中找最小的与第二个位置的数交换，即顺序放在已排好序的数列的最后，如此循环，直到全部数据元素排完为止。
• 实现思路
  1、第1趟比较：拿第1个元素依次和它后面的每个元素进行比较，如果第1个元素大于后面某个元素，交换它们，经过第1趟比较，数组中最小的元素被选出，它被排在第一位
  2、第2趟比较：拿第2个元素依次和它后面的每个元素进行比较，如果第2个元素大于后面某个元素，交换它们，经过第2趟比较，数组中第2小的元素被选出，它被排在第二位
  …
  3、第n-1趟比较：第n-1个元素和第n个元素作比较，如果第n-1个元素大于第n个元素，交换它们
• 示例
  
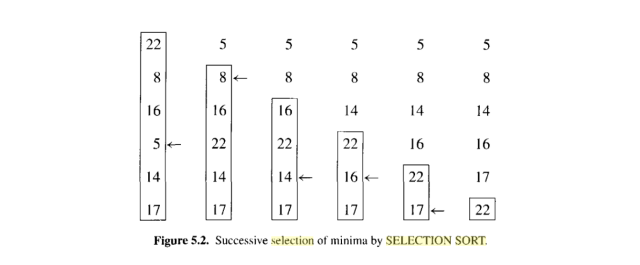
• 代码实现

public static void selectionSort(int[] arr) {
    //一定要记住判断边界条件，很多人不注意这些细节，提高代码健壮性。
    if (arr == null || arr.length < 2) {
        return;
    }
    //第一个循环控制比较总次数
    for(int i = 0; i < arr.length - 1; i++) {
        //第二个循环依次选择元素和第一个元素比较
        for(int j = i + 1; j < arr.length; j++) {
            if(arr[i] > arr[j]) {
                int temp = arr[i];
                arr[i] = arr[j];
                arr[j] = temp;
            }
        }
    }
}

选择排序的核心是，在每趟比较中，找到本趟中**最小的元素**放在本趟比较的第1个位置，所以选择排序的每趟比较只需要交换一次即可。但是，上述代码在每趟比较过程中，一旦发现某个元素比第1位的元素小，就交换它们。徒增了交换的次数。

改进（增加最小元素的下标）：

public static void selectionSort(int[] arr) {

    if (arr == null || arr.length < 2) {
        return;
    }

    for(int i = 0; i < arr.length - 1; i++) {
        //增加最小元素的下标
        int minIndex = i;
        for(int j = i + 1; j < arr.length; j++) {
            if(arr[i] > arr[j]) {
                minIndex = arr[j] < arr[minIndex] ? j : minIndex;
            }
        }

        int temp = arr[i];
        arr[i] = arr[minIndex];
        arr[minIndex] = temp;
    }
}

• 选择排序的不稳定性
  在一趟选择，如果当前元素比一个元素小，而该小的元素又出现在一个和当前元素相等 的元素后面，那么交换后稳定性就被破坏了。比较拗口，举个例子，序列[5 8 5 3 9]，我们知道第一遍选择第1个元素5会和3交换，变成[3 8 5 5 9]。那么原序列中2个5的相对前后顺序就被破坏了，所以选择排序不是一个稳定的排序算法。