求杨辉三角的前n行数据_挖掘习题内涵 渗透数学文化 ——“杨辉三角”的教学实践...

教学背景

数学是人类文化的重要组成部分，数学文化是数学教学不可分割的部分。人教版数学教材里编排了丰富的数学文化知识，除了在“你知道吗”栏目集中呈现外，练习题里也有不少和数学文化有关的题目。如六年级上册第八单元《数与形》的练习里，就有一道关于“杨辉三角”的题目(练习二十二第7题，第111页)：

“杨辉三角”是我国南宋末年杰出的数学家杨辉的一个重要数学研究成果，是二项式系数在三角形中的一种几何排列。它把二项式系数排成三角形的形式，把组合数内在的一些代数性质直观地从图形中体现出来，是一种离散型的数与形的结合。西方有与之相似的“帕斯卡三角”，但杨辉比帕斯卡的发现约早了400年。

在数学教学中渗透数学文化，能“帮助学生了解数学在人类文明发展中的作用，激发数学学习兴趣，感受数学家治学的严谨，欣赏数学的优美。”张奠宙教授指出，数学文化应当结合课程内容来展开。如果仅按照题目的要求，让学生发现数之间的关系并按照发现的规律继续写下去，学生并不能体会“杨辉三角”的伟大，也不能理解其在数学史上为什么会具有如此重要的地位。所以，教师应该采取有效的教学策略，设计与习题相关的问题，帮助学生在问题解决中感受数学文化，在规律探究中欣赏数学文化。

教学实践

1.发现规律

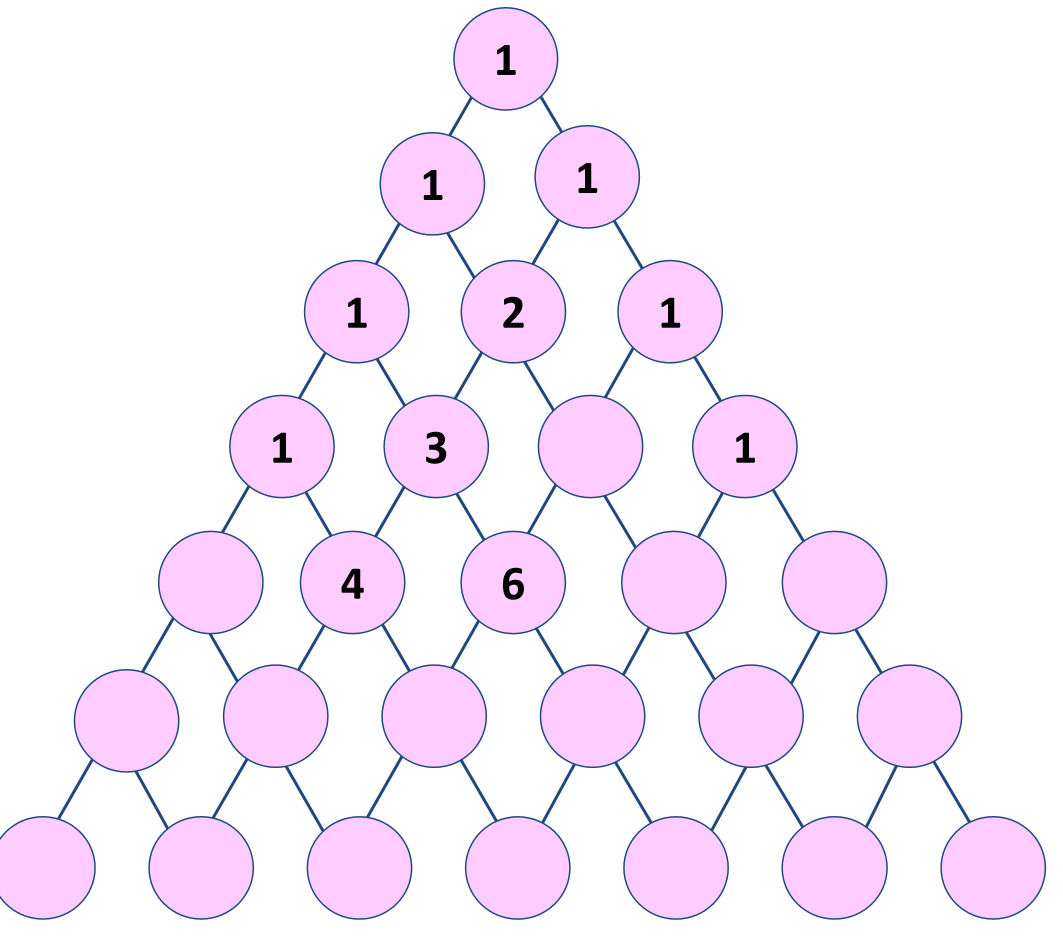
逐层出示下图，师：这是一张三角形的表。把数字排成三角形形状，是我国南宋末年数学家杨辉的创举。数学史上把这样的三角形表称为“杨辉三角”(板书)。大家观察一下，杨辉三角中数字的排列有什么规律？

生答(略)。

师：请大家按照发现的规律，在空的圆圈里填上适当的数。

学生操作，教师根据学生的汇报把三角形表填完整。

2.感受杨辉三角的美

师：有的同学在嘀咕了，这么简单的数字排列，居然被称为创举？同学们，“杨辉三角”的数字和排列规律都非常简单，在数学学习中却又非常有用。虽然相关的一些知识要到中学才学习，但“杨辉三角”一些优美的规律，我们小学生也能去探究。

(1)和2的幂的关系

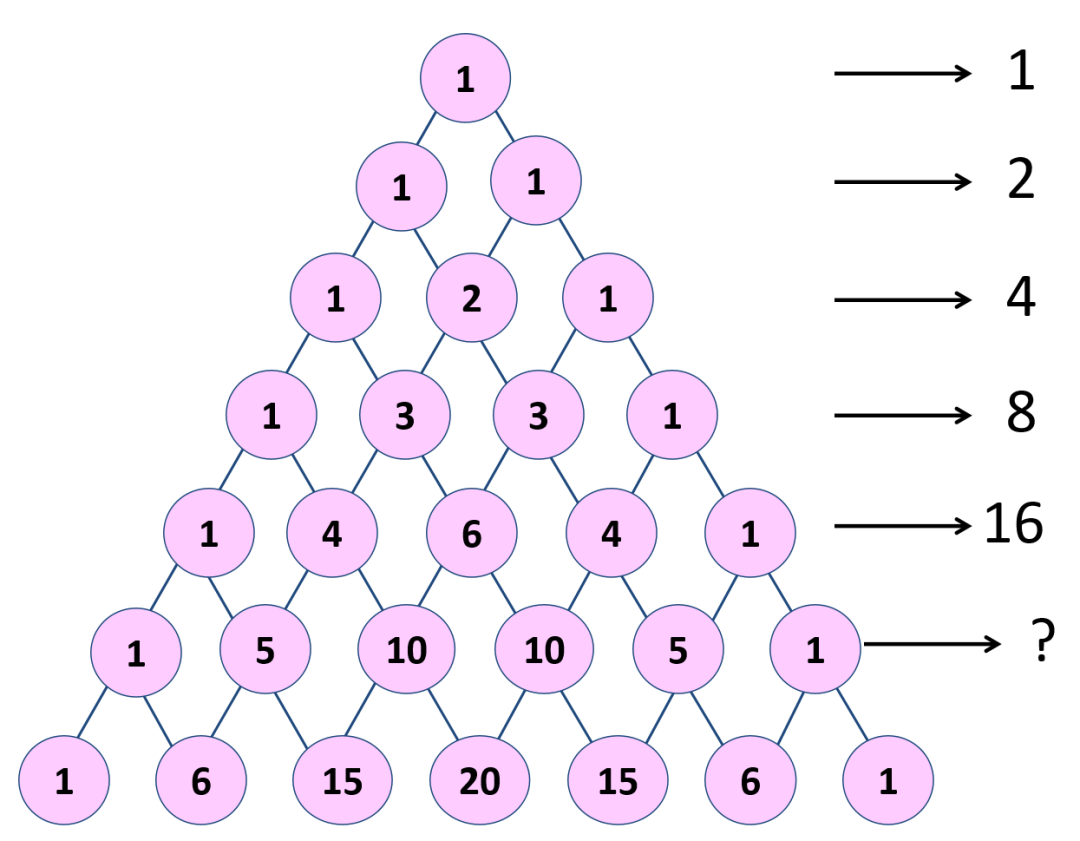
师：请大家横着把前5行每一行数分别相加。

学生操作，反馈，在ppt上呈现答案。

师：有什么发现？能把这些数写成2的几次方的形式吗？

师：猜一猜，下一行整行数的和是几？

生1：32。16×2＝32。

生2：32也就是2的5次方。

师：让我们验证一下。(学生验证)。

师：在数学上，2的0次方就是1。这里每一行的数的和，都可以写成2的几次方形式，第n行数的和就是2的n-1次方。实际上，“杨辉三角”最初就是用来解决两个数或字母相加和的几次方的问题的。

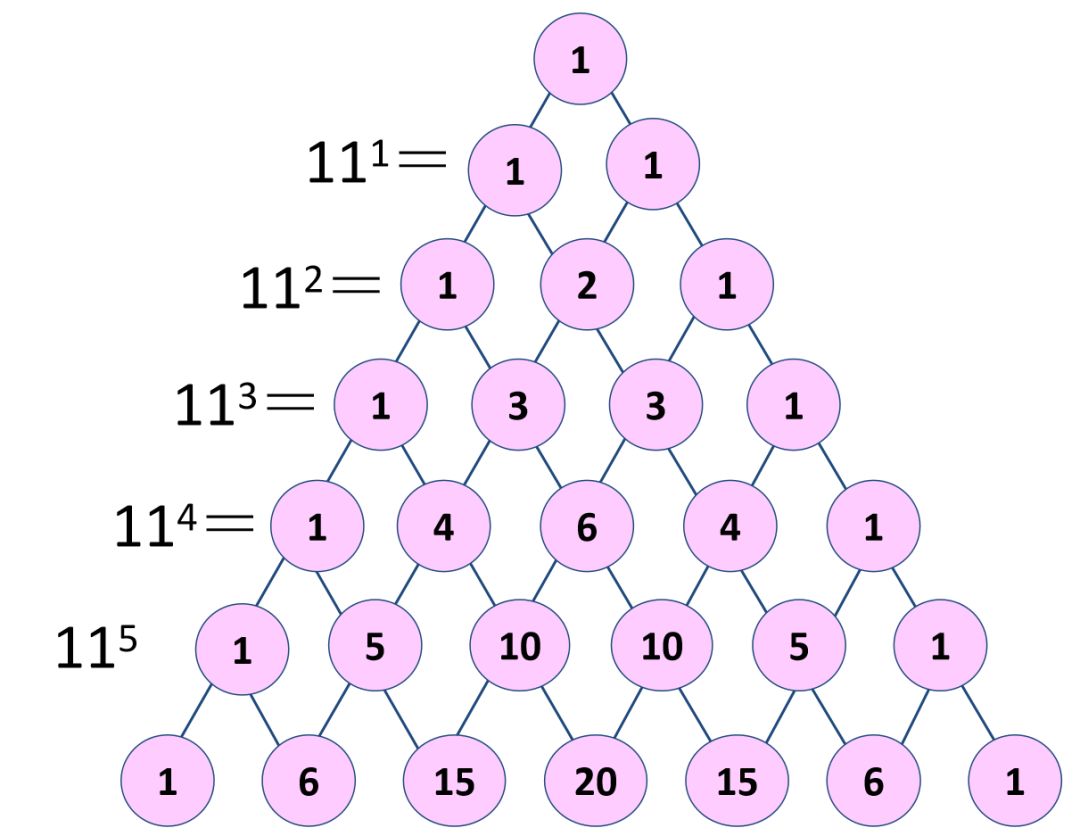
(2)和11的幂的关系

师：你们能口算11的平方吗？

学生马上回答：121。

师：11的3次方呢？

学生迟疑，有的口算，有的列竖式计算。过一会儿，报出答案：1331。

教师微笑着指指“杨辉三角”的第4行，学生一片哗然。

师：11的4次方呢？

生：14641！

师：你怎么算得这么快？

生：杨辉三角的第5行就是这个数。

师：真会思考。我们用计算器验证一下。

师：11的5次方呢？

生：15101051！

教师用计算器计算14641乘11，得到161051。

师：怎么回事？

生：我知道了。这里的6＋4等于10，其实是要向前一位进1的。然后4加6等于10，加上1是11，写1进1；5加1等于6，所以是161051。

教师在ppt上演示，得出杨辉三角中的数字是正确的，但由于要满十进一，所以最后写出来的数发生了变化。

(3)和三角形数、四面体数的关系

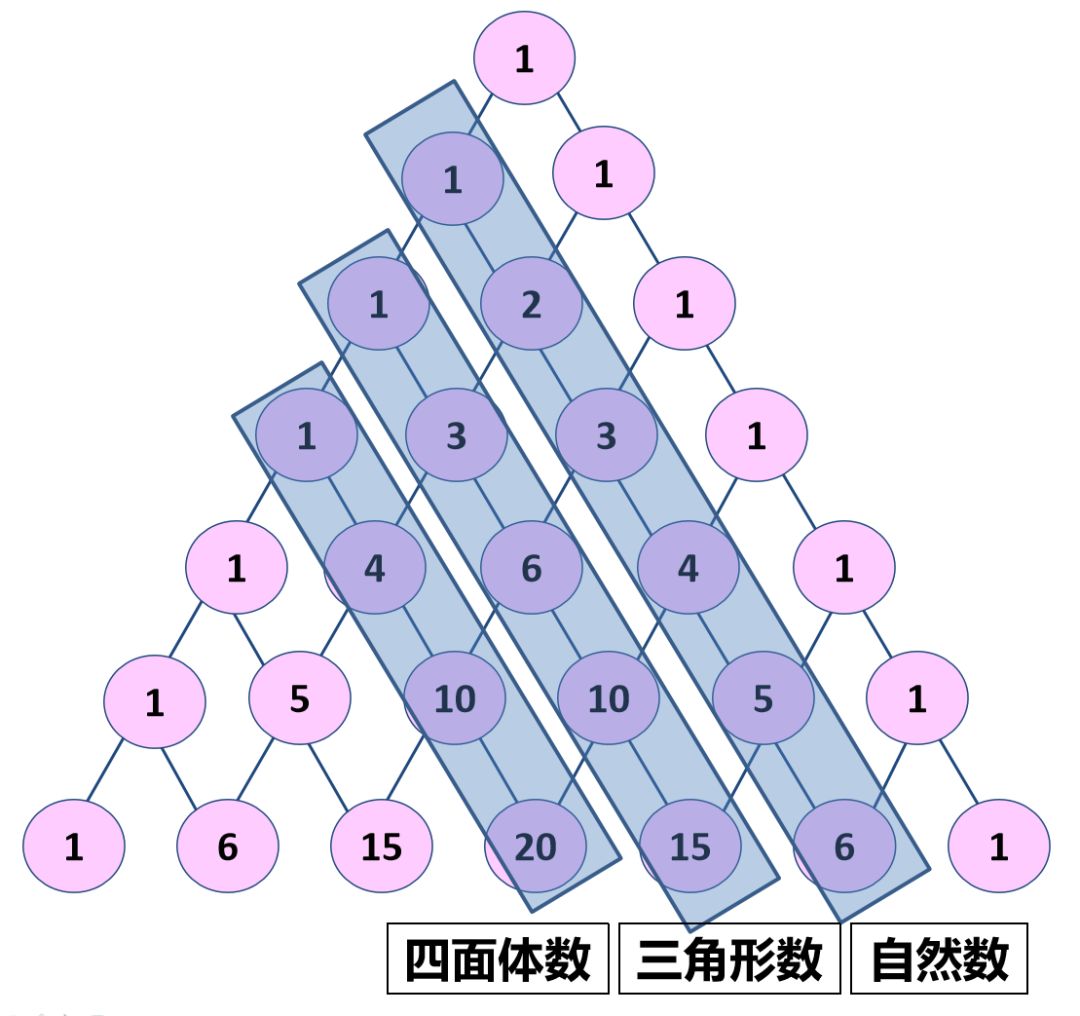
教师演示：斜着看，有什么发现？

生：第一列都是1，第二列一个一个大起来，第三列是加2、加3、加4，第四列是加3、加6、加10……，都是有规律的。

师：右边(或左边)第二列都是自然数序列，右边(或左边)第三列都是三角形数序列。请大家翻到书本第109页，看到练习二十二第2题。

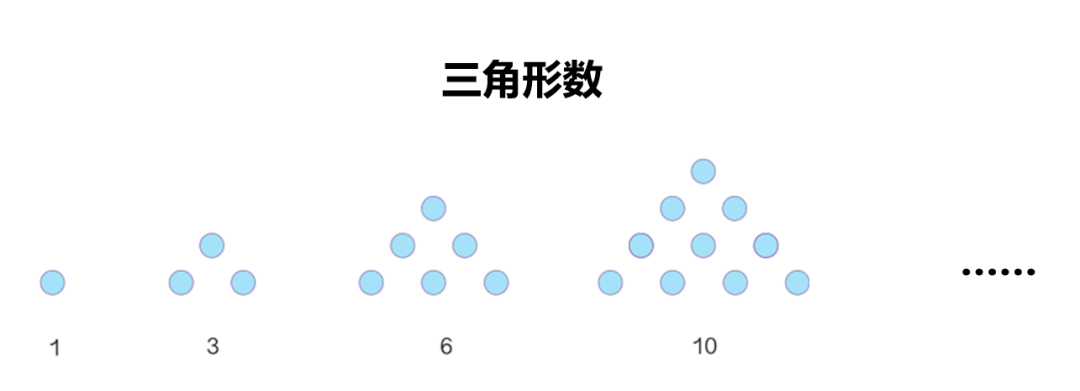
师：接下来的一个三角形数是15，请同学们用图表示出15。(学生画，略)

师：下两个三角形数分别是什么？请画图表示。

学生操作(略)。

师：右边(或左边)第四列都是四面体数，我们欣赏一下

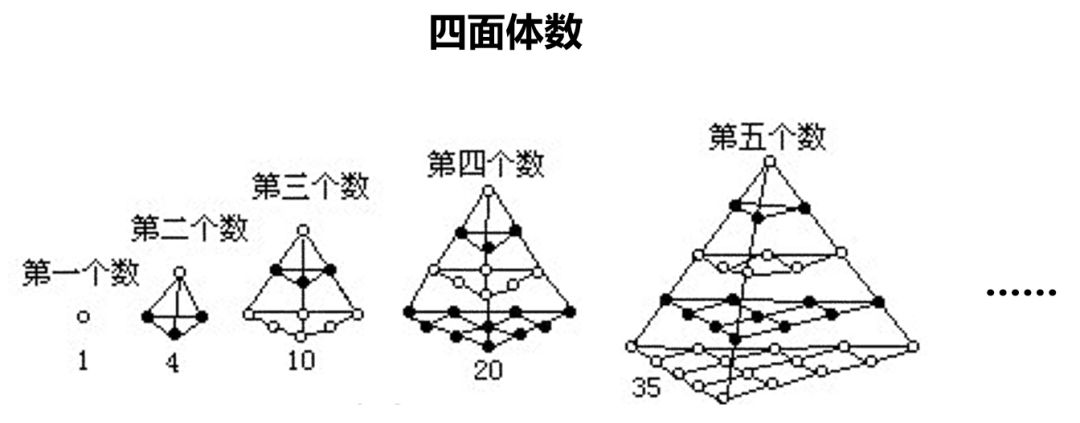
(4)和斐波那契数列的关系

把杨辉三角形适当变形，观察图中的数据，发现这是一个斐波那契数列。

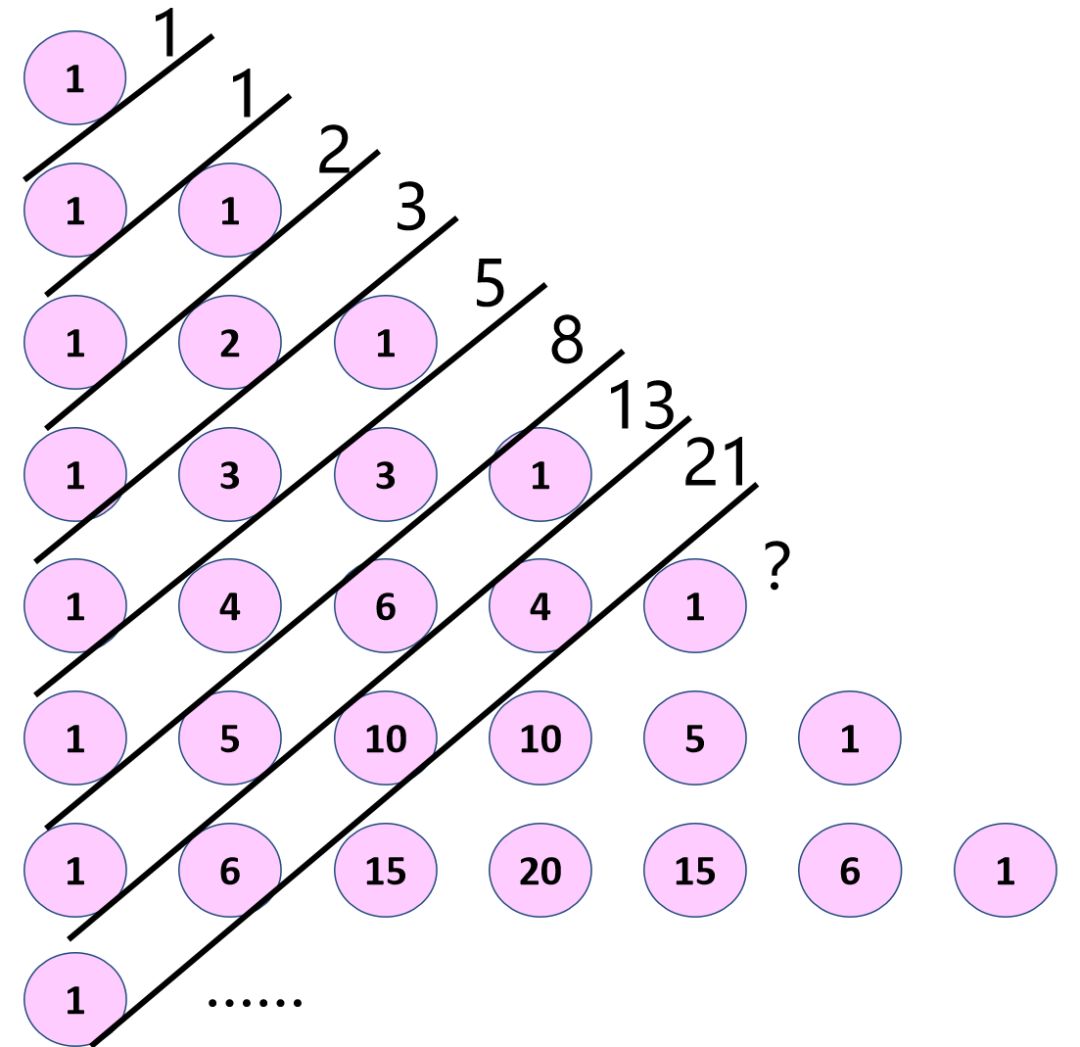
3.杨辉三角的应用

师：“杨辉三角”利用数与形的巧妙统一，在解决一些数学问题时可以起到很好的作用。我们来看下面的例子：

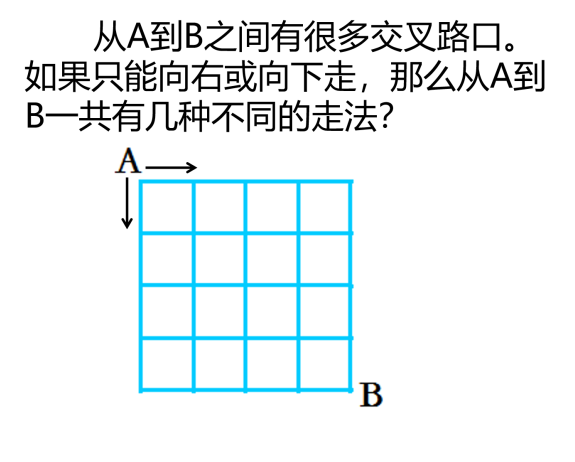
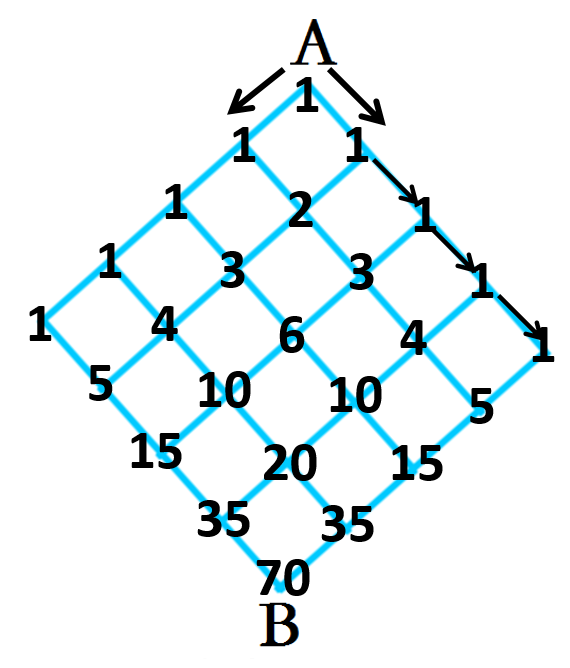
学生尝试操作，会发现比较困难。教师提示：把图顺时针旋转45°，转化为类似“杨辉三角”的图形，把每一个交叉点上的走法标出来，用“杨辉三角”的知识来解决(图5-2)。

教后体会

“杨辉三角”是中国古代数学史上光辉灿烂的一页。带领学生探寻“杨辉三角”的奥秘，不仅能加深对“杨辉三角”的认识，还可以让学生更好地感受数与形之间的相互作用，受到数学文化的熏陶。英国数学家格雷舍指出：“如果任何一门学科将与它的历史割裂开来的企图得逞的话，我相信，没有哪门学科比数学的损失更大。”如果教师能充分认识数学习题里蕴含的数学文化价值，以问题引领，让学生经历探究数学规律的过程，就能帮助学生更好地感受数学文化，欣赏数学文化，体会数学的思想、精神和价值。