实对称矩阵的特征值求法_机器学习和线性代数 - 特征值和特征向量

特征值和特征向量可能是线性代数中最重要的概念之一。从机器学习、量子计算、物理到许多数学和工程的问题，都可以通过找到一个矩阵的特征值和特征向量来解决。

根据定义(标量λ、向量v是特征值、特征向量A)：

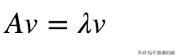
视觉上，Av与特征向量v位于同一直线上。

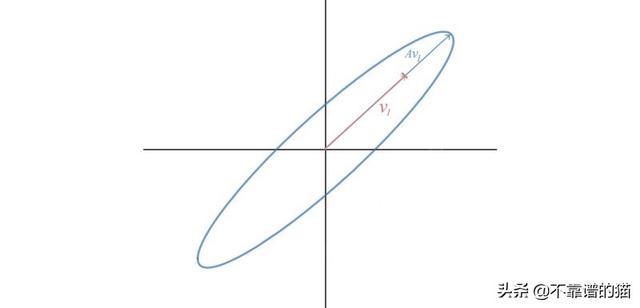
这里有些例子。

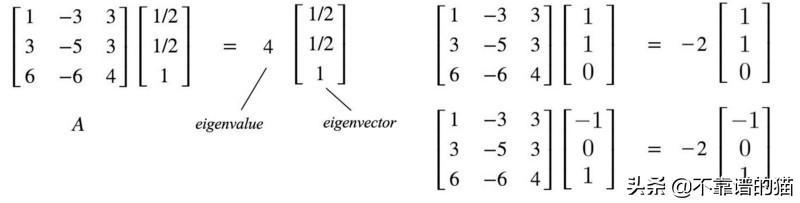
然而,Ax通常不会等于λx。只有一些特殊的向量满足条件。

应用

许多问题可以用线性变换建模，其中解决方案来自特征值和特征向量。让我们先用一个抽象的例子来详细说明这个问题。在许多系统中，我们可以在向量中表达属性，其变化率线性地取决于当前属性(例如，人口增长率线性地取决于当前人口和GDP)。一般等式是

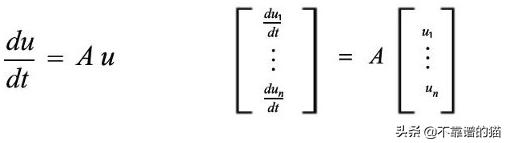
我们来猜一下满足上面方程的u(t)。因为一个指数函数的导数等于它本身，我们从一个t的指数函数开始然后乘以一个向量x，输出就是一个向量。

根据上面的计算，u(t)的解是

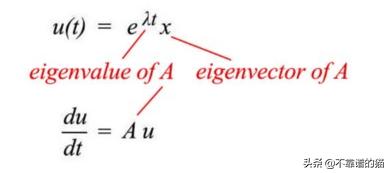
接下来，我们将找到它的完全解。一阶导数方程是一个线性函数。

对于线性函数，完全解是特定解的线性组合。如果u和v是解，则C₁u + C₂v也是解。从我们之前的特征值λ= 4，-2和-2的例子中，完全解将是

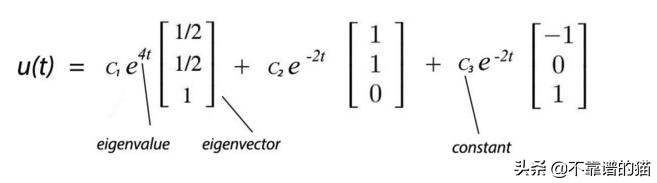
在t = 0时,我们可以测量初始状态u(0),比如说[u₀₁,u₀₂,u₀₃]ᵀ,并求解常数C₁,C₂,C₃。

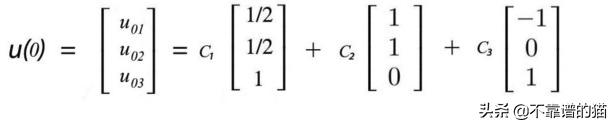
让我们用谐振子来说明这个想法。我们选择这个例子是因为谐波振荡器及其近亲(量子谐振子)在研究粒子物理学，量子力学或物理学方面几乎无处不在。我们从著名的F=ma方程开始用特征值和特征向量来解二阶导数。由于我们确实可以自由选择质量单位，物理学家通常设m = 1来简化讨论，即

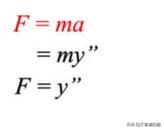
我们把谐振子问题重新写成矩阵的形式。