快速排序算法详细图解_算法——快速排序

最新推荐文章于 2025-10-18 22:52:03 发布

最新推荐文章于 2025-10-18 22:52:03 发布 · 559 阅读

文章标签：

#快速排序算法详细图解

本文详细介绍了快速排序算法，包括其分治策略、排序过程，并提供了参考代码。快速排序是一种高效的原地排序算法，通过选取轴值将序列划分为两部分，然后递归地对子序列进行排序。

快速排序作为应用最为广泛的排序算法，实现简单，而且能够比其他同类算法快速很多。除此之外，它只需要一个很小的辅助栈就可以实现原地排序，所以快速排序是一种时空兼达的算法。但它的缺点是不够稳定，非常脆弱，很多错误都能够只是它在实际的性能只有平方级别。好了，让我们一起来学习一下这种既美丽又需要十分小心的算法吧！

一、分治策略

①划分

选定一个记录作为轴值(pivot)，以轴值为基准将整个序列划分为两个子序列

…

和

…

，前一个子序列中记录的值均小于或等于轴值，后一个子序列中记录的值均大于或等于轴值；

②求解子问题

分别对划分后的每一个子序列递归处理；

③合并

由于对子序列

…

和

…

的排序是就地进行的，所以合并不需要执行任何操作。

划分示意图

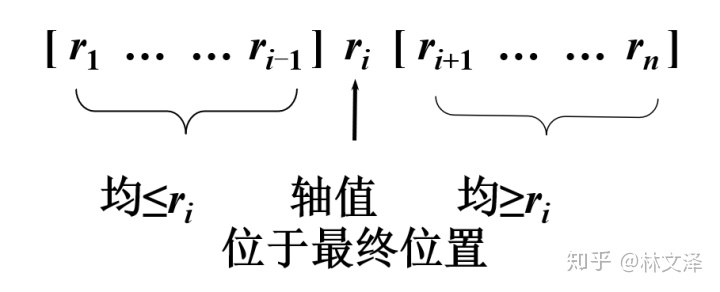
归并排序按照记录在序列中的位置对序列进行划分

快速排序按照记录的值对序列进行划分

具体讲解过程可见：快速排序讲解视频

二、排序过程

以第一个记录作为轴值，对待排序序列进行划分的过程为：

（1）初始化：取第一个记录作为基准，设置两个参数i，j分别用来指示将要与基准记录进行比较的左侧记录位置和右侧记录位置，也就是本次划分的区间；

（2）右侧扫描过程：将基准记录与j指向的记录进行比较，如果j指向记录的关键码大，则j前移一个记录位置。重复右侧扫描过程，直到右侧的记录小（即反序），若i＜j，则将基准记录与j指向的记录进行交换；

（3）左侧扫描过程：将基准记录与i指向的记录进行比较，如果i指向记录的关键码小，则i后移一个记录位置。重复左侧扫描过程，直到左侧的记录大（即反序），若i＜j，则将基准记录与i指向的记录交换；

（4）重复（2）（3）步，直到i与j指向同一位置，即基准记录最终的位置。

三、参考代码

void QuickSort(int r[ ], int first, int end)
  {
     if (first<end) {      
        pivot=Partition(r, first, end);  
          //问题分解，pivot是轴值在序列中的位置
        QuickSort(r, first, pivot-1); 
          //递归地对左侧子序列进行快速排序
        QuickSort(r, pivot+1, end);
          //递归地对右侧子序列进行快速排序
     }
  }
     

 int Partition(int r[ ], int first, int end)
     {
          i=first; j=end;         //初始化
          while (i<j)
          {  
       while (i<j && r[i]<= r[j]) j--；  //右侧扫描
               if (i<j) { 
                  r[i]←→r[j];            //将较小记录交换到前面
                  i++; 
               }
              while (i<j && r[i]<= r[j]) i++；  //左侧扫描 
               if (i<j) {
                  r[j]←→r[i];            //将较大记录交换到后面
                  j--; 
               }
           }
          retutn i;    // i为轴值记录的最终位置
    }