本文介绍计算图的概念及其在神经网络中的应用，探讨自动求导原理并提供Python实现，展示了如何搭建多层全连接神经网络进行MNIST手写数字识别。
前言
本文节选自即将出版的《深入理解神经网络——从逻辑回归到CNN》（暂定名）的第八章“计算图”。阅读本文前，可先阅读本专栏之前的文章“神经网络反向传播算法”和“梯度下降”。本文介绍了计算图以及计算图上的自动求导（通用的反向传播）的原理，用Python+Numpy实现了计算图以及计算图上的反向传播，用其搭建了一个多层全连接神经网络，建模 MNIST 手写数字识别。本文的样例代码见于：
张觉非/计算图框架gitee.com
在下一篇博文中：
张觉非：运用计算图搭建 LR、NN、Wide & Deep、FM、FFM 和 DeepFMzhuanlan.zhihu.com
我们用这个框架搭建几个非全连接的神经网络，包括LR、Wide & Deep、FM、FFM 以及 DeepFM 。本文的代码相比较于书中的代码会有不同，因为交稿后作者还在持续修改。我们有望推出下一本书，教读者实现一个基于计算图的机器学习框架。
神经网络的结构并不仅限于多层全连接，在深度学习领域，存在局部连接、权值共享、跳跃连接等丰富多样的神经元连接方式，多层全连接仅仅是其中的一种。在打开更广阔的新世界的大门之前，我们首先需要掌握描述和训练任意神经网络的方法。
计算图是一个强大的工具，绝大部分神经网络都可以用计算图描述。计算图用节点表示变量，用有向边表示计算。自动求导应用链式法则求某节点对其他节点的雅可比矩阵，它从结果节点开始，沿着计算路径向前追溯，逐节点计算雅可比。将神经网络和损失函数连接成一个计算图，则它的输入、输出和参数都是节点，可利用自动求导求损失值对网络参数的雅可比，从而得到梯度。
本文首先介绍计算图，并以多层全连接神经网络和一种非全连接网络为例，展示计算图的表达能力，之后，我们介绍自动求导的原理和实现。具备了这些知识，就能理解如何构建和训练任意神经网络，为进入深度学习领域做好准备。
1 计算图模型
我们需要一种灵活通用的方法描述各种神经网络，计算图就是一种合适的工具。本节首先介绍计算图的基本概念，之后阐述如何用计算图描述多层全连接神经网络以及一个简单的卷积神经网络。
1.1 简介
计算图（computational graph）是一种有向无环图（directed acyclic graph，DAG）。计算图用节点表示变量，用有向边（directed edge）表示计算。有向边的目的节点称为子节点，源节点称为父节点，计算图定义如何用父节点计算子节点，如图1所示。
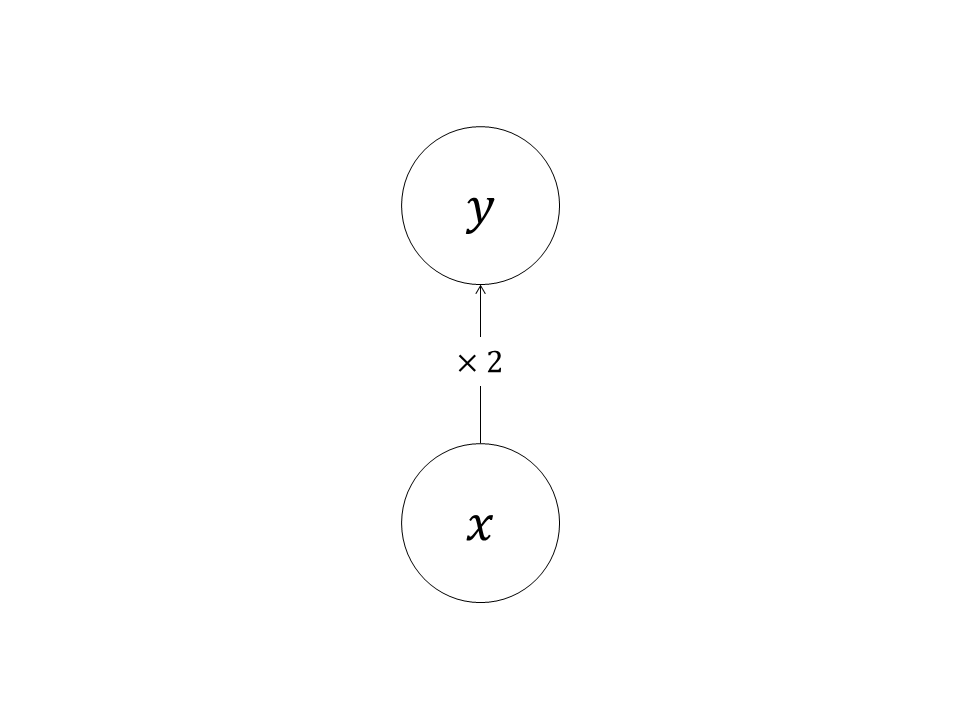
图1中的计算图描述了计算：
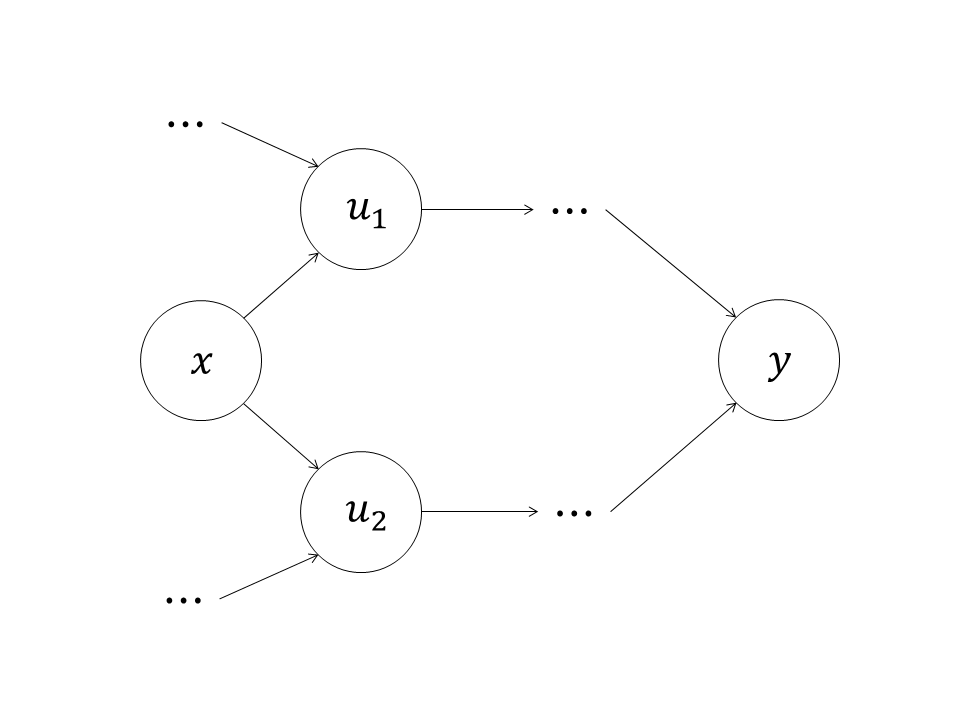
一个子节点可以有两个父节点，表示该子节点由两个父节点计算而得，如图2所示。
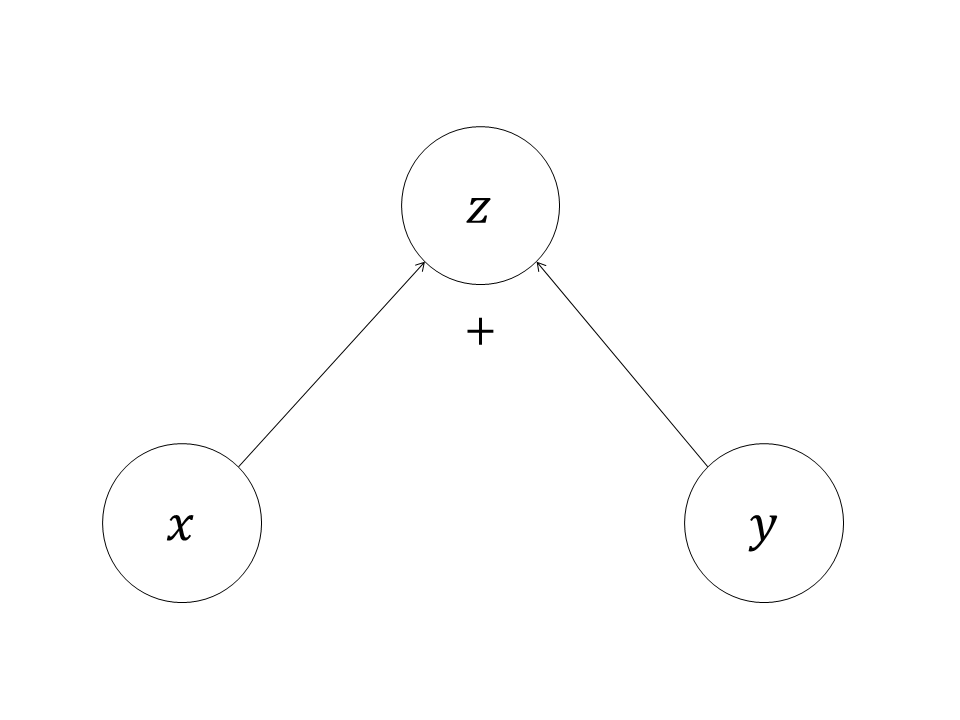
图2中的计算图描述的计算是：
一个子节点也可以有两个以上的父节点，但是这种情况可以通过添加中间节点而转化成每个子节点只有两个父节点的情况。图3中的两个计算图是等价的。
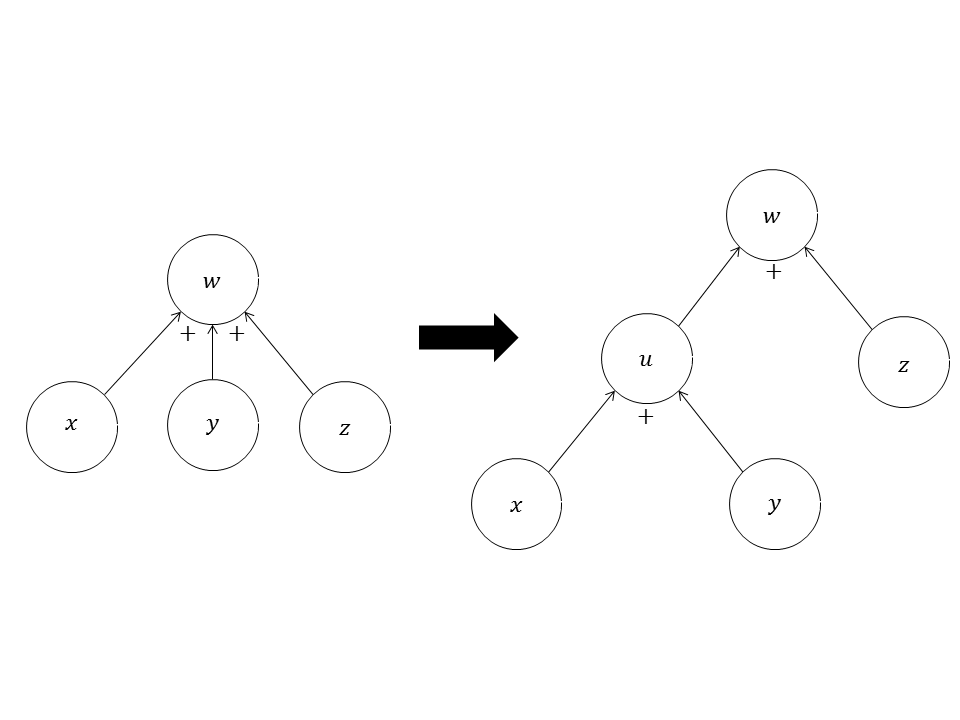
图3中的两个计算图描述的计算都是：
所以本文中，每个子节点至多有两个父节点。用上述简单的组件可以表达复杂的计算，例如图4所示。
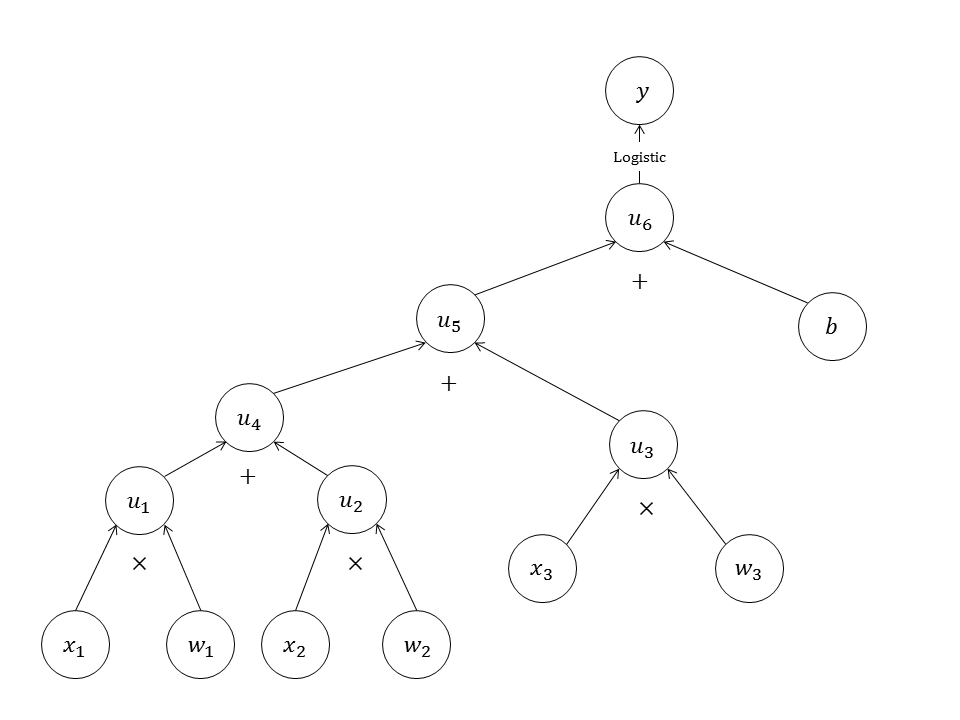
图4中的计算图表示逻辑回归模型：
同一个计算可以用不同的计算图描述。计算式可以代数变形这自不必说，即便是同一个式子也可以用不同的计算图描述，这取决于表示计算的“粒度”。例如图4中，从节点得到节点的计算是Logistic函数，但也可以将Logistic函数拆解成更基础的计算，如图5所示。
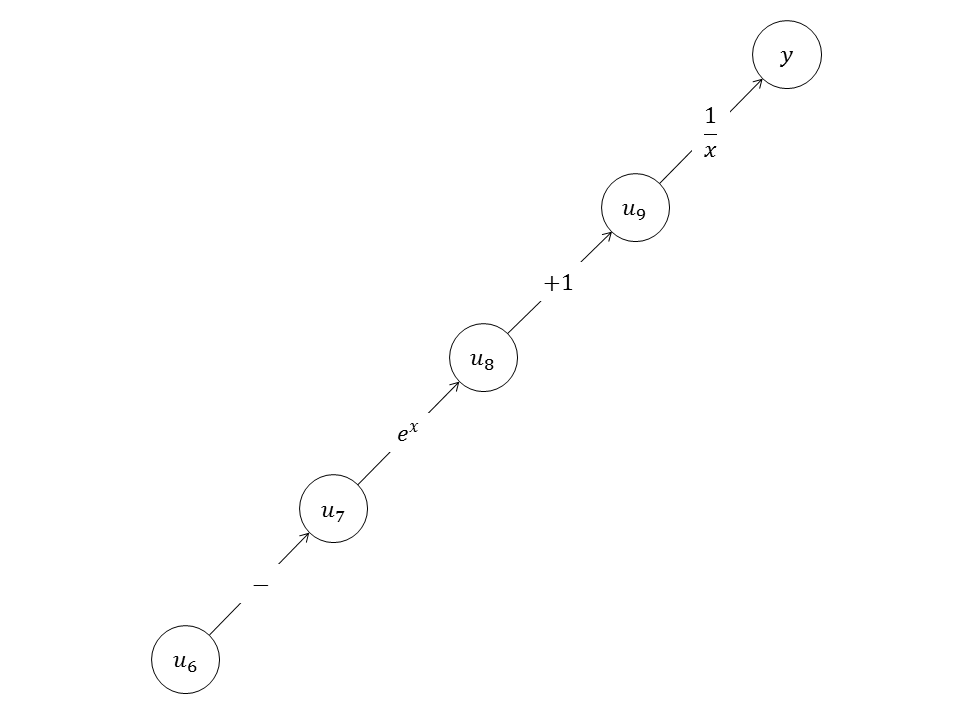
图5中的计算图只包含取反、指数、增1和取倒数这四种基础运算，它表示的是Logistic函数。用更基础的运算构建计算图，会使计算图的规模更大。以上介绍的计算图的节点都是标量，节点也可以是向量、矩阵乃至张量（tensor）。可将矩阵或张量的元素重新排列为向量，例如矩阵：
将的元素重新排列，可以得到向量：
向量
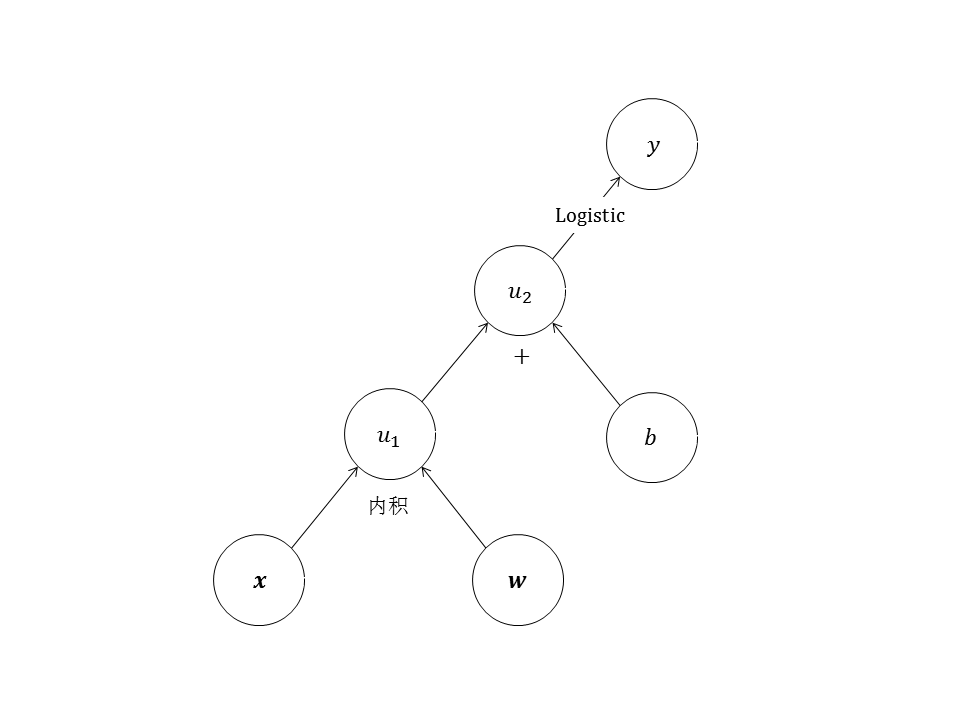
图6中的
如果计算图有多个输入节点，可将其中一部分输入节点视为变量，将其他输入节点视为常量。例如图6中的逻辑回归计算图，预测时将
1.2 多层全连接神经网络的计算图
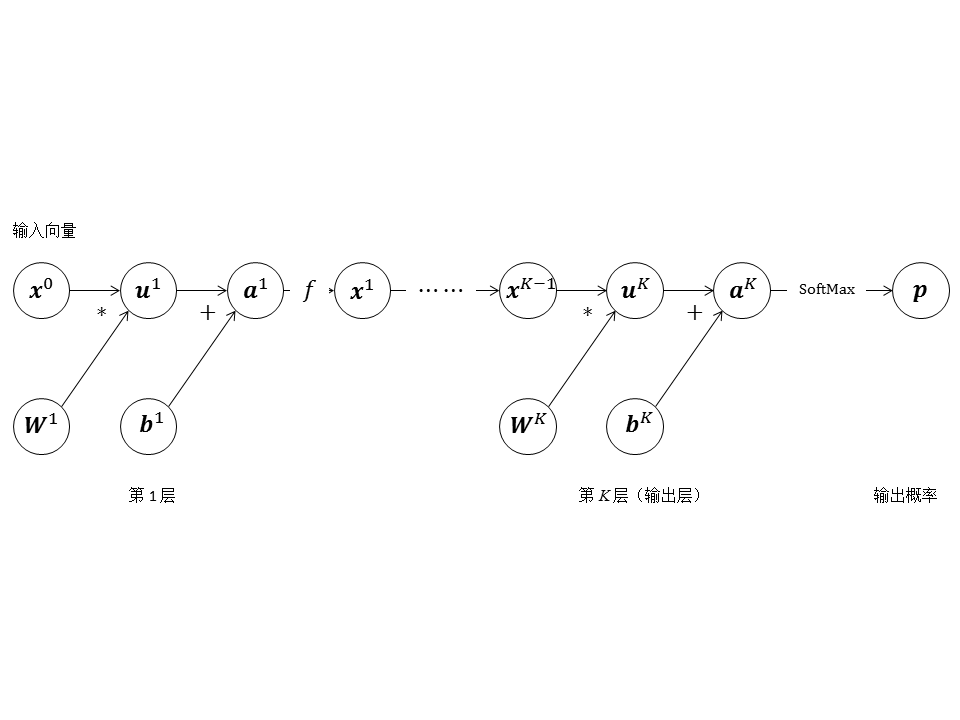
常见的多层全连接神经网络示意图就是一个计算图，它的节点都是标量，表示计算的粒度较细。现在我们可以用向量节点更简洁地表示多层全连接神经网络，如图7所示。
1.3 其他神经网络结构的计算图
计算图可以灵活地表达各种复杂的神经网络，本节举一个例子，请看图8所示的神经网络。
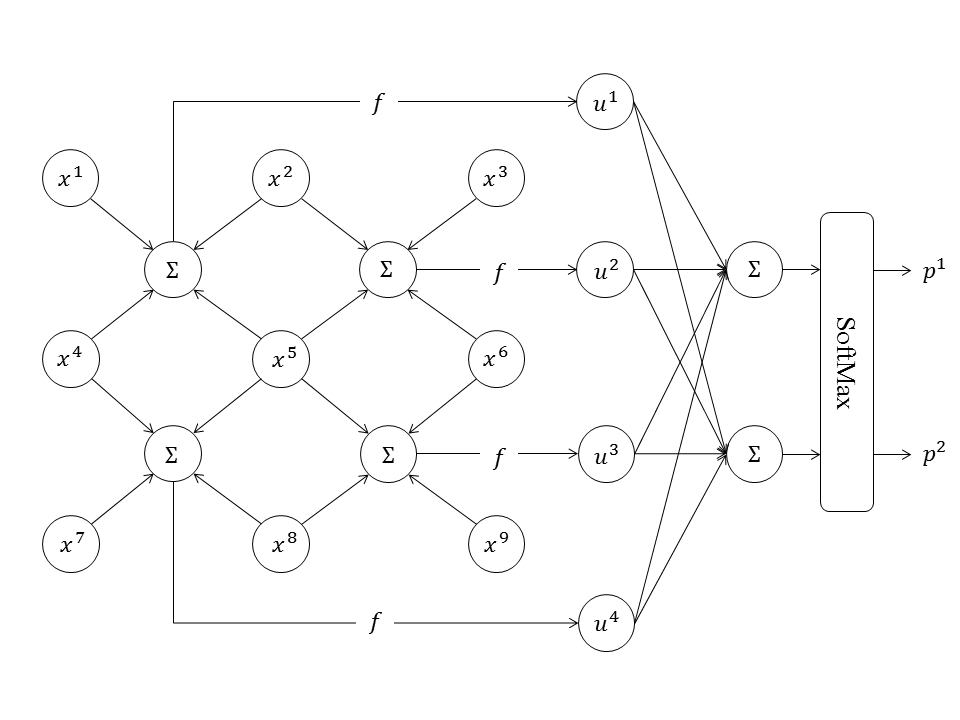
这个神经网络的输入是
由于我们将计算限制为矩阵/向量的加法和乘法以及激活函数，而没有其他类型的计算，故该计算图稍复杂。如果加入更多的计算类型，则可以更简洁地表示这个卷积神经网络，但是这个例子说明计算图足以表达复杂的神经网络。
2 自动求导
对于计算图中的任意节点
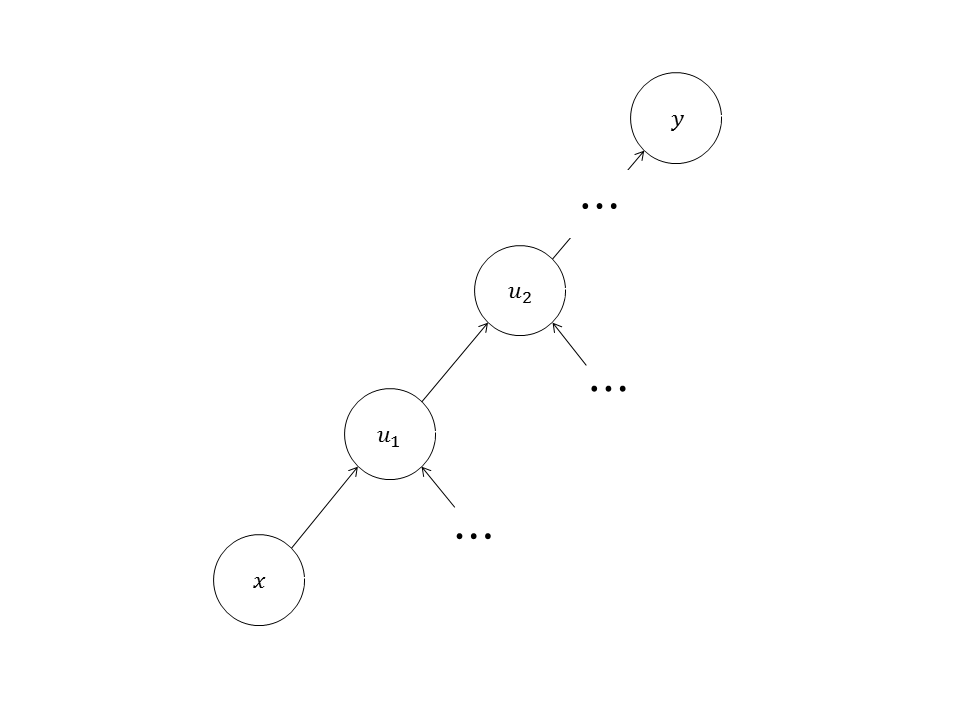
图10省略了计算图的其他部分。由
本文用偏导数相同的符号表示雅可比矩阵，例如
如果一个节点有多个子节点，如图11所示，
根据链式法则，
如果有两个以上子节点，同样可以证明：
这对于自动求导非常有利：如果一个节点有多个子节点，将结果节点对这些子节点的雅可比与这些子节点对该节点的雅可比相乘再求和，就得到了结果节点对该节点的雅可比。有时需要计算
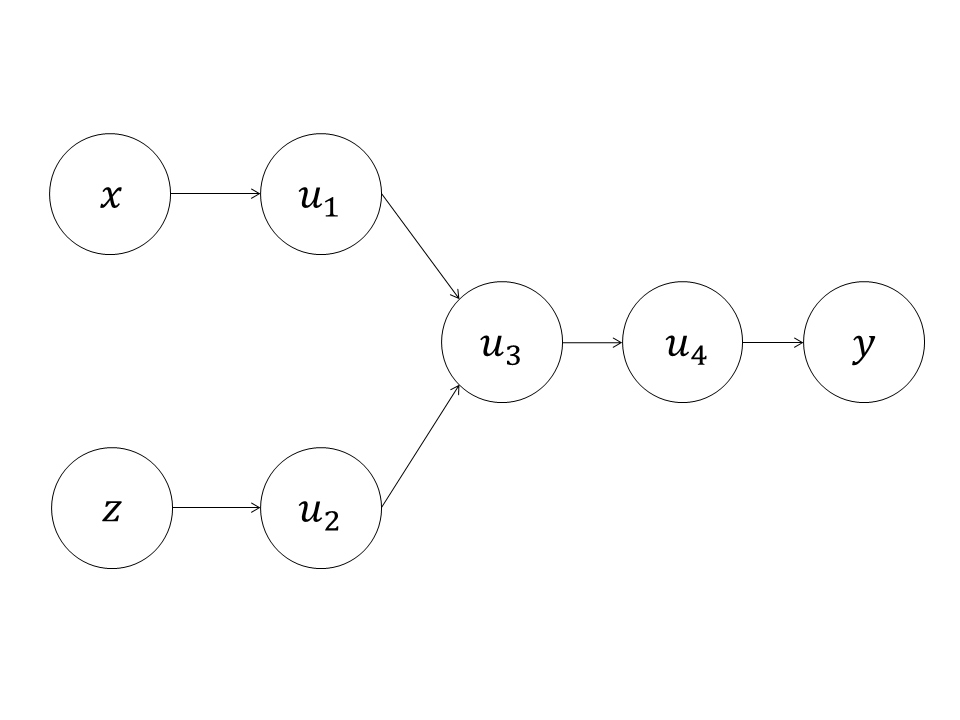
假设图12中的
该式会被计算两次，如果将其结果保存起来，则可以节省计算量。这就是自动求导的核心所在：保存结果节点对计算路径上各个节点的雅可比，并用它们计算结果节点对更上游节点的雅可比。中间节点的雅可比就是被“反向传播”的对象，计算图自动求导是广义的反向传播。
3 自动求导的实现
本节讨论计算图自动求导的实现，我们以面向对象式的伪代码来描述该实现。节点是对象，它包含两个属性：value 和 jacobi。value 包含本节点的值，如果本节点尚未被计算，则 value 是 NULL。jacobi 包含结果节点对本节点的雅可比，如果雅可比尚未被计算，则 jacobi 为 NULL。节点有如下方法。
计算节点的值，如果有父节点的值尚未计算，则抛出异常；
返回所有子节点，若无子节点则返回空集；
返回所有父节点，若无父节点则返回空集；
接受一个父节点，计算本节点对这个父节点的雅可比。注意本方法与属性的区别，是结果节点对本节点的雅可比，是计算并返回本节点对某个父节点的雅可比。
若要计算某个节点的值，则它的所有父节点必须先被计算。信息沿着计算图路径从前向后传播，这就相当于神经网络的前向传播。以下 forward_propagation 函数实现了计算某节点值的前向传播过程。
function 节点的 evaluate() 执行的计算可以是标量计算，矩阵/向量计算或者其他更复杂的计算，忽略各种计算的差异，将它们的时间复杂度都视为
若要计算某个节点对它的某个上游节点的雅可比，则沿着计算图路径从后向前，逐节点计算结果节点对它们的雅可比。在所有子节点的雅可比计算完成后，则父节点的雅可比可以计算。中间节点的雅可比可能会被使用多次，将它们保存在对象属性（jacobi）中，可避免重复计算。以下 back_propagation 函数计算节点对某个上游节点的雅可比。
function get_jacobi 对计算路径上的每条边执行一次，
现在我们用原生Python和Numpy库实现计算图以及自动求导，并用计算图搭建多层全连接神经网络。与TensorFlow不同，我们的节点不是三维乃至更高维度的张量（Tensor），而是矩阵（包括向量和标量）。根据之前的讨论，原则上只用矩阵就可以实现任何计算。首先，我们实现计算图节点的基类，代码如下：
import 代码中，Graph类是计算图类，default_graph对象是一个全局的计算图对象，它们的实现我们稍后呈现。Node类是计算图节点的基类，所有类型的节点都继承自Node类。Node类实现了计算图节点的一些公共方法，它的构造函数接受可变数量的Node类对象，作为本节点的父节点，本节点的值用这些父节点的值计算而得。
节点对象保存父节点和子节点的引用列表，这是构成计算图的“边”的关键数据结构。利用它们，就可以遍历计算图。value和jacobi是节点的属性，分别保存节点的值和某个被视为最终结果的节点对本节点的雅可比矩阵。若它们为空，则表示尚没有被计算。构造函数将通过参数传进来的节点加入本节点的父节点列表，再将本节点加入所有父节点的子节点列表，最后将本节点加入计算图对象的节点列表。
接下来是一些简单的设置和获取方法，不必赘述。forward是执行前向传播，计算本节点的值的方法，它是第3节的伪代码的实现。为了计算本节点的值，forward方法首先检查父节点的值是否为空，若某个父节点的值为空，则递归调用该父节点的forward方法。确保所有父节点的值都已被计算后，forward方法调用compute方法计算本节点的值。在基类中，compute方法是一个抽象方法，需要具体的节点子类去覆盖实现各种不同的计算。get_jacobi方法是另一个抽象方法，它接受一个父节点，计算当前本节点对这个父节点的雅可比矩阵。
backward方法是实现反向传播的关键，它接受一个被视为计算图计算结果的节点，计算当前该结果节点对本节点的雅可比矩阵。backward方法是第3节的伪代码的实现。若本节点的jacobi属性为空，则表示结果节点对本节点的雅可比矩阵尚未被计算。若本节点就是结果节点，则雅可比矩阵为单位矩阵，否则利用链式法则根据结果节点对各个子节点的雅可比矩阵计算结果节点对本节点的雅可比矩阵。
接下来的两个方法容易理解，不再赘述。reset_value方法将本节点的值置空。因为本节点的值影响下游节点的值，所以应该递归置空所有下游节点的值。是否递归取决于参数recursive。
有了基类，我们就可以实现各种不同的节点类，它们执行不同计算。我们首先实现Variable类，它保存一个变量。Variable对象没有父节点，它们是计算图的终端节点。可以随机初始化Variable对象的值，也可以为Variable对象赋值。Variable类的代码如下：
class Variable类的构造函数接受dim参数，确定变量的形状。init参数表示是否要随机初始化变量的值。trainable参数表示本变量节点是否参与训练。set_value方法为Variable类独有，它设置变量的值。若变量的值被改变，则计算图中所有下游节点的值都将作废，所以set_value方法调用reset_value方法递归清除本节点以及所有下游节点的值。Variable对象的值是被赋予或被随机初始化的，所以它不用实现compute方法。Variable对象没有父节点，它也不用实现get_jacobi方法。接下来我们实现向量加法节点，代码如下：
class Add 类的compute方法将两个父节点的值相加。get_jacobi方法求当前Add对象对某一个父节点的雅可比矩阵。向量加法是一个
class 在我们的实现中，值一律采用numpy.matrix类型，即矩阵。
所以有：
内积对某个向量的雅可比矩阵是另一个向量的转置，这就是Dot类的get_jacobi方法所返回的值。矩阵相乘节点的代码如下：
class 之前讨论原理时我们提到过，不论输入输出的形状是什么，一个计算节点都可以视作向量到向量的映射，只不过我们需要将矩阵展平。例如一个
class 可以利用Logistic函数的值方便地求得其导数。Logistic类的get_jacobi方法利用已经计算好的value成员计算对父节点的雅可比矩阵。该雅可比矩阵是一个对角矩阵，对角线元素是Logistic函数对父节点某个元素的导数。类似地，ReLU节点的代码如下：
class ReLU节点的值和雅可比矩阵都很容易计算，代码自明，不再赘述。接下来，我们实现SoftMax节点，代码如下：
class SoftMax节点执行的计算我们已经很熟悉了，但是我们不实现它的get_jacobi方法，因为计算SoftMax函数对输入向量的雅可比矩阵较复杂，但是如果将SoftMax函数的输出送给交叉熵，计算交叉熵损失对SoftMax函数的输入向量的雅可比矩阵是相当简单的，所以我们实现一个将SoftMax函数与交叉熵损失合二为一的节点类，代码如下：
class CrossEntropyWithSoftMax节点的compute方法对第一个父节点的值施加SoftMax函数，再与第二个父节点的值计算交叉熵。第二个父节点的值是类别标签的One-Hot编码向量。get_jacobi方法对第一个父节点计算雅可比，对第二个父节点的雅可比矩阵不会被使用，但是也实现在此。
至此，我们实现了几种典型的计算图节点，它们对于我们接下来要做的事情已经足够。有兴趣的读者可以自己实现一些其他类型的节点。接下来我们实现Graph类，代码如下：
import 我们的Graph类较简单，它只保留计算图的全部节点，实现清除所有节点的雅可比矩阵和值的方法。default_graph是一个全局的Graph对象，默认情况下所有节点都将被加入到default_graph中。最后，我们实现训练优化器类。所有优化器类都继承自一个基类，代码如下：
from Optimizer类的构造函数接受一个Graph对象，一个作为优化目标的节点对象，以及Mini Batch的样本数量。因为我们的计算图节点只能包含一个向量，所以不能利用更高的维度在节点值中包含整个Mini Batch。于是，我们对Mini Batch的实现是这样的：对一个Mini Batch中的样本依次执行前向传播和反向传播，将参与训练的变量的梯度累加在acc_gradient中，一个Mini Batch计算完毕后执行变量更新，这时使用Mini Batch中多个样本的平均梯度。
one_step方法调用forward_backward方法对一个样本执行前向传播和反向传播，将目标节点对各个变量的梯度累加在acc_gradient中，最后清除所有节点的雅可比矩阵。one_step方法计数样本数，当样本数达到batch_size时，执行update方法更新变量，并清除累加梯度以及计数。get_gradient方法返回一个Mini Batch的所有样本的平均梯度。
update是抽象方法，利用Mini Batch的平均梯度以各种不同的方法更新变量值。update方法将在具体的优化器类中得到实现。forward_backward方法执行前向传播，计算目标节点的值，然后反向传播计算目标节点对每个参与训练的变量节点的雅可比矩阵。原始梯度下降的优化器实现如下：
class 除了Optimizer 类的参数，GradientDescent类的构造函数还接受learning_rate参数，即学习率。GradientDescent类的update方法相当简单，就是获得平均梯度，乘以学习率并取反后更新到变量节点的当前值上。RMSProp和Adam优化器的代码如下：
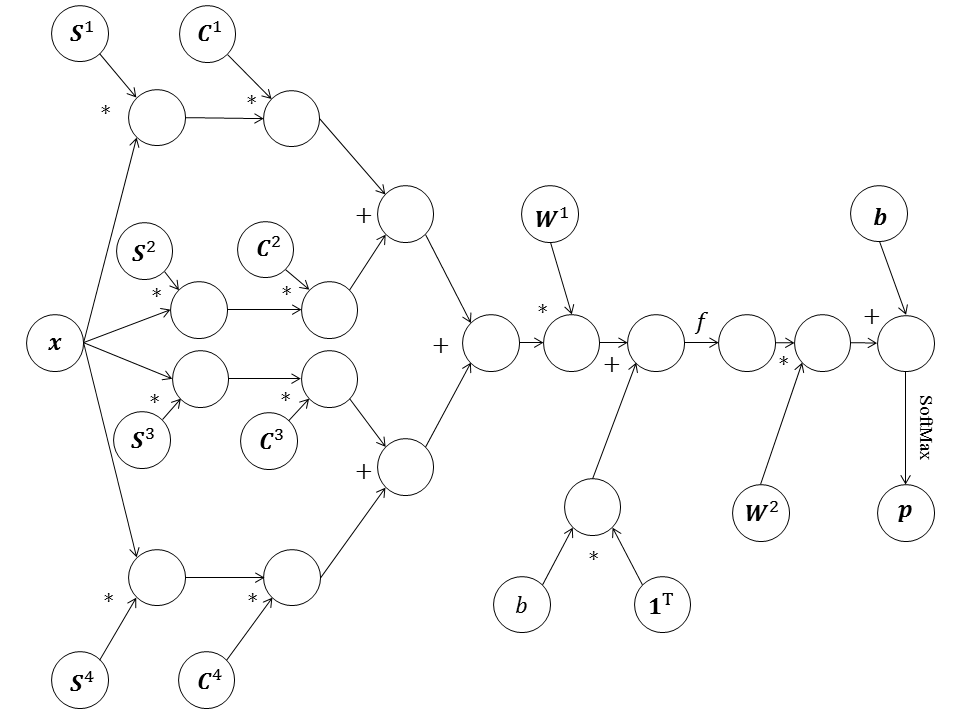
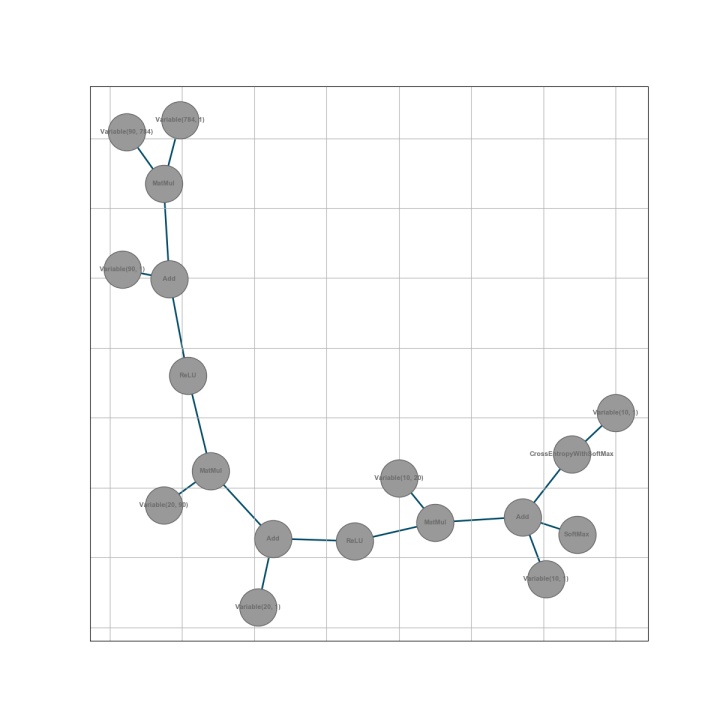
class 关于RMSProp和Adam，专栏之前的文章已经有了详细论述和Python实现，这里只是把相同逻辑实现在我们的计算图优化器框架内，就不再详细解释了。有兴趣的读者可以自己实现其他优化器。最后，我们用这个计算图框架搭建一个多层全连接神经网络，并用它分类MNIST手写数字，代码如下：
import 我们将这个神经网络的计算图绘制出来：
4 小结
本文介绍了计算图，大部分神经网络都可以用计算图表示。以计算图中的一个节点为最终结果，可以计算它对其他节点的雅可比，这就是计算图的自动求导。在神经网络语境下，自动求导可看作是广义的反向传播。
扫一扫
955
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
