
0.基本情况介绍
numpy作为一个高效率的矩阵计算工具,除了基本的加减乘除以及切片外,还有比较独特的索引功能。索引功能我们比较常见有序号索引以及转置,如下:
import numpy as np
arr = np.arange(20).reshape(4,5)
##
建立了一个4行5列的矩阵
##索引取其中的第4、3、1、2行
arr[[3,2,0,1]]
##获取其转置矩阵
arr.T
##变成了5行4列的矩阵
1.升级
当我们开始遇到多维数组时,题目中提到的transpose和swapaxes就开始发挥作用了。
1.1 transpose 按照多维数组的轴的索引进行变换。
乍一听是不是有点绕,别急,慢慢来。首先我们来了解下多维数组的轴是什么东东?
对于多维数组来说,一个维度就是一个轴。
我们知道一维为一条线,二维为一个平面,三维为一个空间,到四维已经超越了我们人类肉眼能够观测的空间。
- 对于一维数组来说,有一个轴,如 arr1 = np.array([1,2,3,4]),
arr1.ndim = 1 arr1.shape = (4,)
- 对于二维数组来说,有两个轴,如arr2 = np.array([[1,2,3,4],
[5,6,7,8]]),
arr1.ndim = 2 arr2.shape = (2,4)
- 对于三维数组来说,有三个轴,如arr3 = np.array([[[1,2,3,4],
[5,6,7,8]],
[[9,10,11,12],
[13,14,15,16]]]),
arr2.ndim = 3 arr3.shape = (2,2,4)
是否大概对轴有一个直观的了解?
言归正传,对于transpose来说,会将多维数组的轴编号,也就是给各个轴建立索引,我们自设一个三维数组,维数为(2,2,4),有三个轴:
arr = np.arange(16).reshape(2,2,4)


当我们进行变换时,有 arr.transpose(2,1,0),这里就是让索引2变换到了索引0的位置,索引0变到了索引2的位置,索引1保持不变,根据索引的变动,形状也发生相关位置的变化,如下:
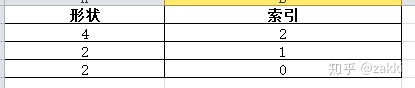
这个时候,我们的多维数组就变成了:

1.2 swapaxes 对轴进行两两置换
理解了上面的transpose,应该再理解swapaxes就不难了。swapaxes实际上也是针对轴索引进行变化,区别就在于transpose可以一次搞三个,但是swapaxes只能两两置换。
对于swapaxes来说,括号内的两参数,交换位置和不交换,实际结果相同。
接上例:
arr.swapaxes(1,2)(实际上等价于arr.swapaxes(2,1)),那么原多维数组就变为:

也就是:
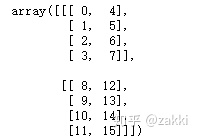




 这篇博客介绍了numpy中的维度交换操作,包括transpose和swapaxes。文章通过实例解释了轴的概念,以及如何使用transpose按照轴的索引进行变换。同时,详细阐述了swapaxes函数,它允许两两轴之间的置换,与transpose的区别在于swapaxes仅能交换两个轴的位置。
这篇博客介绍了numpy中的维度交换操作,包括transpose和swapaxes。文章通过实例解释了轴的概念,以及如何使用transpose按照轴的索引进行变换。同时,详细阐述了swapaxes函数,它允许两两轴之间的置换,与transpose的区别在于swapaxes仅能交换两个轴的位置。

















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








