如何将有向图转化为无向图_有向图的学习笔记1 动态更新

最近山东大学开展了有向图的讨论课程，我在这也总结一些我研究生上课时候用的教材和这次学习的体会，机会难得，非常期待第二本书的作者Jorgen Bang-Jensen讲网络流这一块，这一块我一直理解的不透彻。借着这次机会学习。我主要用下面两本的教材：

1 教材分析 （不断更新）

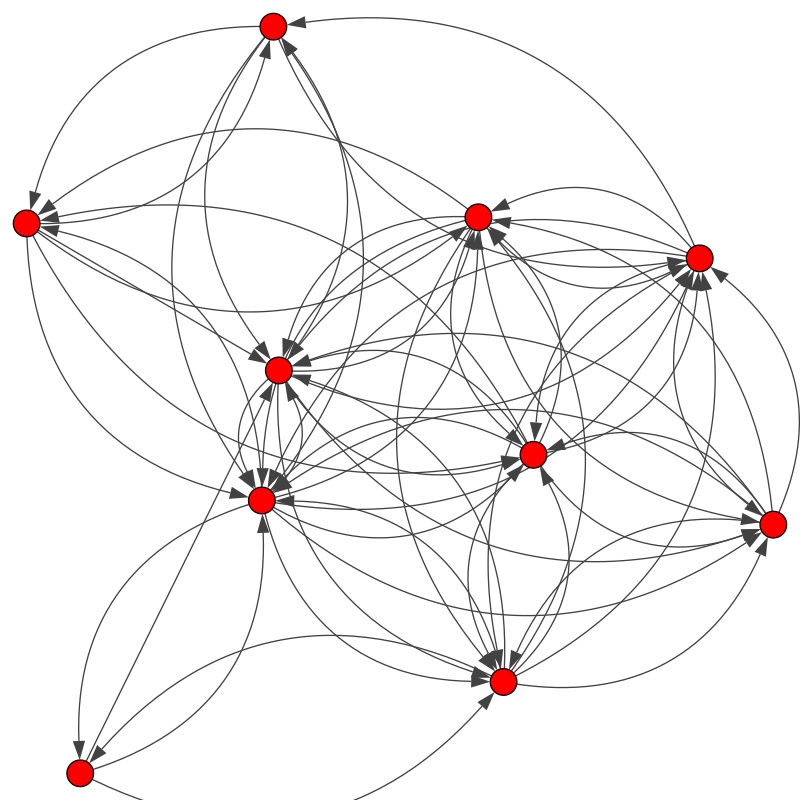
例1：

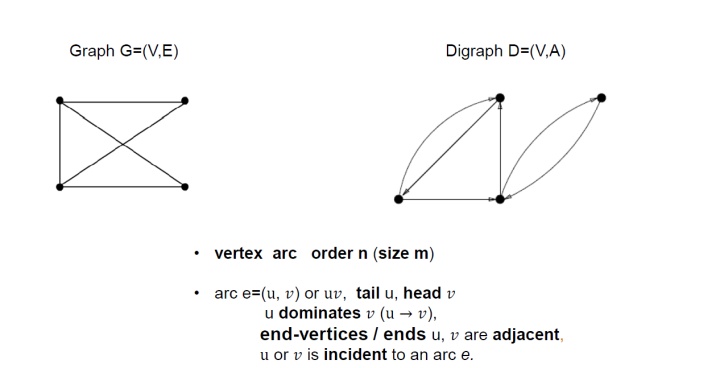
图中

是环弧，

是平行弧，

作为反向弧。

可以用例1的例子尝试解释上面说的概念。注意

的出度是2，入度为3.

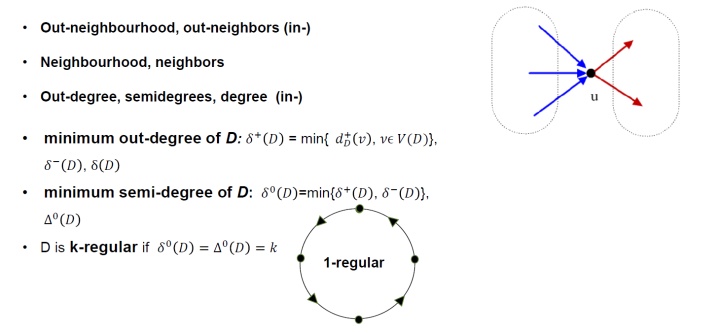
下面定理前半部分顶点的度和等于边数的两倍，类似于无向图的握手引理。定理8.1.1 对于任何有向图

,都有

且

定义8.1.5 与有向图的概念相对应，边不带有方向的图称为无向图．
给定一个无向图

,给它的每条边

确定一个方向，便可得到一个有向图，这个有向图称为

的一个

定向图，而

称为这个有向图的

基础图或底图 (underlying graph).

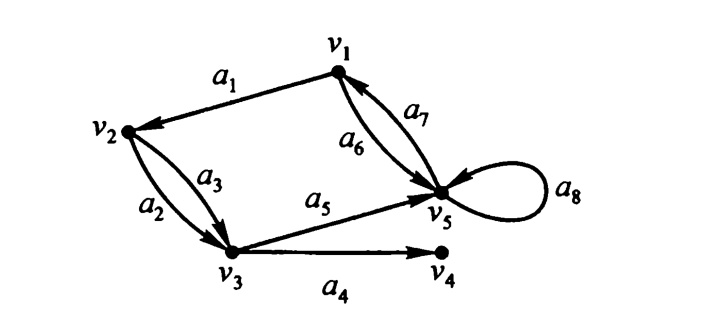
定义8.2.1有向图的一条有向途径是指一个有限非空序列

，它的各项交替地是顶点和弧，使得

．弧不重复的有向途径称为有向迹；顶点不重复的有向途径称为有向路；首尾相接的有向路称为有向圈．

注 有向图的底图中有长的路未必该有向图中就有长的有向路．例如，下图所示的有向图 其底图中的最长路为6，但其最长有向路的长为1.

令人惊奇的是，有向图中·有向路的长却与其底图的色数有关．

定理8.2.1 (Vitaver, 1962; Roy, 1967; Gallai, 1968) 以图

为底图的有向图

中必有长为

的有向路．

额外收获 利用这个定理可以直接推导出山大预备课程所留下的作业:

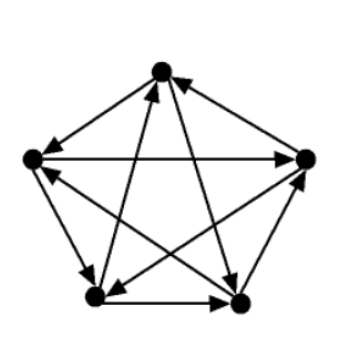
简要说明：tournamnet 是竞赛图的意思，它的底图是完全图，染色数是

，那么该图含了长度为

的有向路，这个有向路就是哈密尔顿路，所以这个图是traceable的。

定理8.2.2 (

) 若

是无环有向图，若其底图

无孤立点，则底图

中必有一个独立集

使得对

中的每个顶点

,存在

，在

中从

到

有长不超过

的有向路．

2 第一次预备课的要点 (重点）

第一节课的听课要点：先是两个经典有趣的问题作为开始。这一块在高中竞赛涉及比较多。

1 图论起源： 戈尼斯堡七桥问题 欧拉问题

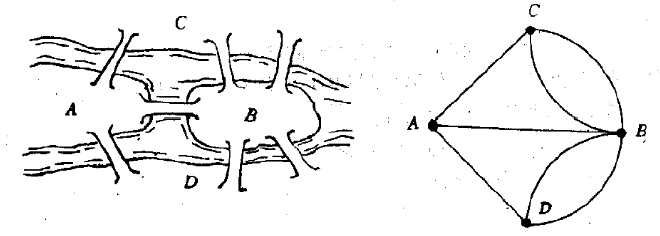
小岛与河的两岸有七条桥连接。在所有桥都只能走一遍的前提下，如何才能把这个地方所有的桥都走遍？

2 哈密尔顿问题

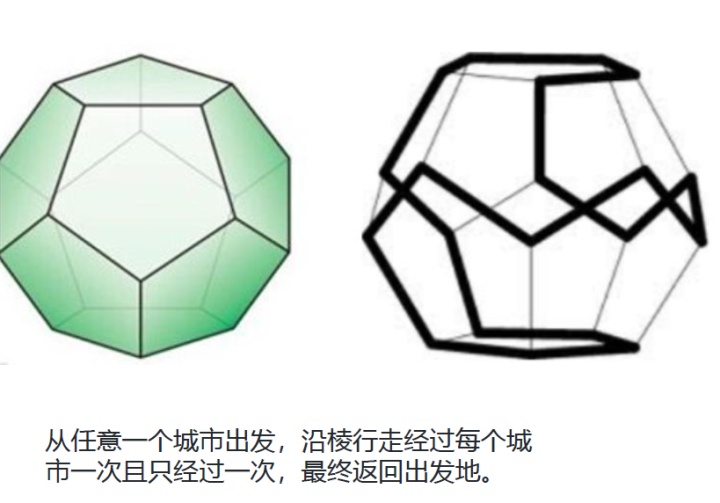
一个哈密尔顿圈有趣的应用。

竞赛图：竞赛图是通过在无向完整图中为每个边缘分配方向而获得的有向图（有向图）。 也就是说，它是一个完整图形的方向，等价于一个有向图，其中每对不同的顶点通过单个有向边连接，即每对顶点之间都有一条边相连的有向图称为竞赛图。设

为

阶有向简单图，若

中基图为n阶无向完全图，则称

是

阶竞赛图。

5阶竞赛图

2.1 主要内容 （第一节）

预备课的目录

基础定义记号1

基础定义记号2

基础定义记号3

predecessor: 代表的前驱 successor 代表后继。比如你看第三张ppt顶点1的前驱就是2和5. 后继就是4和5. 这张ppt重点在于理解walk, triail 和 path. 这个无向图是类似的。 walk,点边均可重复的序列。triail边不重复，点可以重复，path点边均不可重复。
注意如果严格要求点不重复，那么边肯定也是不会重复的。 这里面的欧拉迹和无向图也是类似的。Girth是最短圈的个数，上图的Girth为2， 最长圈是5.

子图，母图，支撑子图。点支撑子图，弧支撑子图

构成上图都

cycle factor

下面的符号在书本证明反复用到：

•

is the set of arcs with tail in and head in

表示尾在

,头在

的弧集合.

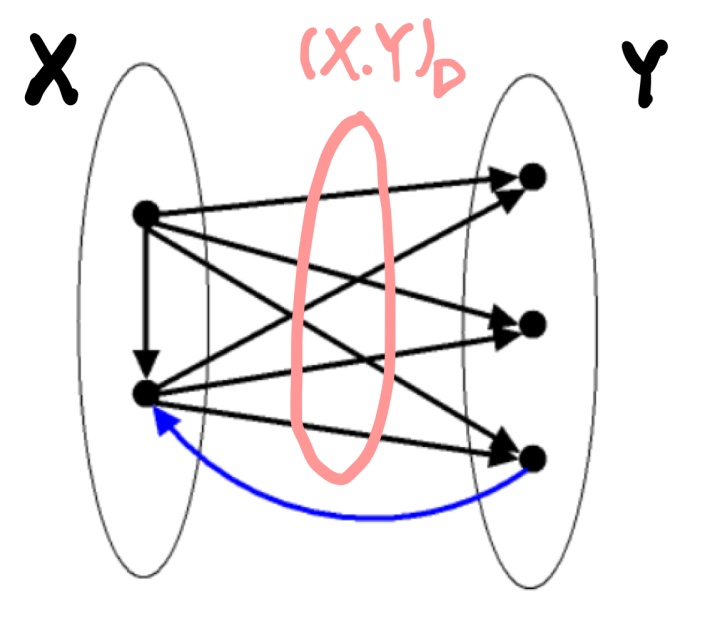
• → : every vertex of X dominates every vertex of

的每一个点都控制

的所有点. 并不关心

内部点或者

是否控制

.

• ⇒ :

= ∅

下图第二个；没有出现图一出现蓝色的边。也就是Y不出现控制X的点.

• ↦ : → ⇒

第二个和第三个条件同时满足。

顶点划分 partiton

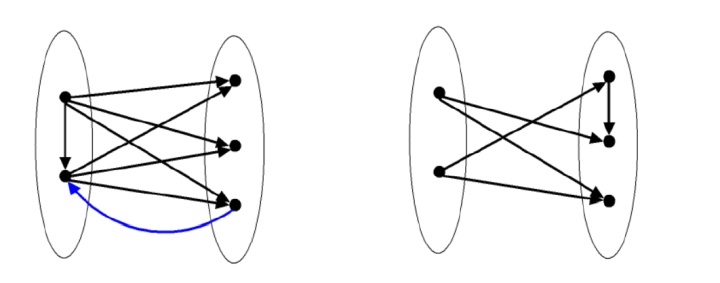
A digraph

is

strongly connected (or, just, strong) if, for every pair

of distinct vertices in

, there existsan

-

walk and a

-

walk.

walk： 可以改成path，因图中存在walk总可以经过一些操作使得点不重复，得到path.

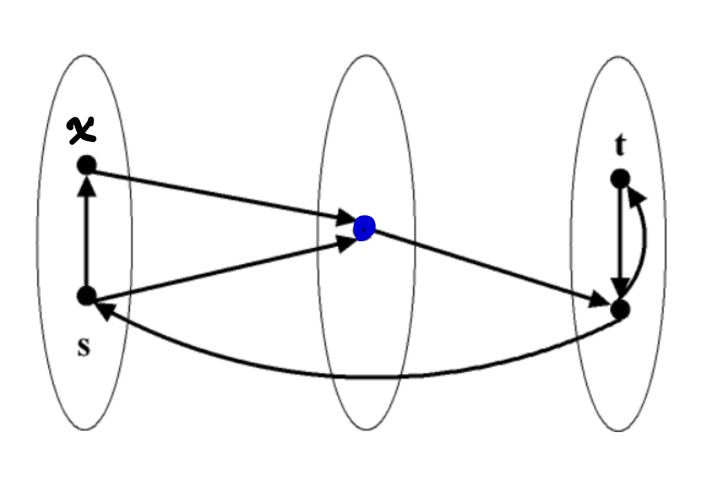
• A set S ⊂ V is a separator (or a separating set set) if − is not strong.

上图可以验证任意两点都相互有路可达，所以该图是强连通的，中间的蓝色顶点是一个separator，去掉之后第一部分的

没有路可以到达

.

• A digraph D is

-strongly connected (or

-strong) if

and D

has no separator with less than k vertices.

上图是1-strong图

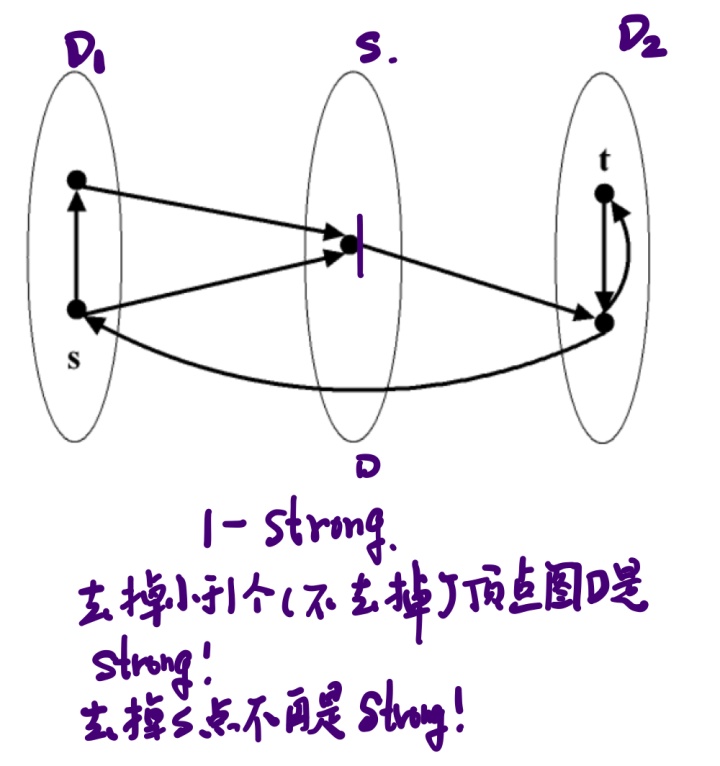
• The largest integer

such that D is

-strongly connected is the vertex strong connectivity of D , denoted by

. (

,

is not stong.)

一个图是

strong,则必然

strong。

• For a pair

of distinct vertices of a digraph D, a set

is an

separator

if

has has no

paths

类似的对于边也可以定义边割集.

•For a strong digraph

, a set of arcs ⊆ is a cut (or a cutset ) if

is not strong.

•A digraph D is k arc strong (or

arc strongly connected ) if

has no cut with less than

arcs.

•arc strong connectivity of D :

•A strong component of a digraph

is a maximal induced subdigraph of

which is strong

•A digraph D is acyclic if it has no cycle.

•acyclic ordering

: if for every arc

in D , we have

; j;

下面的事实说明 无圈图必定存在无圈序。

Proposition1(page14): Every acyclic digraph has an acyclic ordering of its vertices.

证明：We give a constructive proof by describing a procedure that generates an acyclic ordering of the vertices in an acyclic digraph D. At the first step, we choose a vertex v with in-degree zero. (Such a vertex exists by Proposition 1.4.2.) Set

and delete

from D. At the

th step, we find a vertex u of in-degree zero in the remaining acyclic digraph, set

and delete

from the remaining acyclic digraph.

The procedure has

steps. Suppose that

in D, but i > j. As xj was chosen before xi, it means that xj was not of in-degree zero at the jth step of the procedure; a contradiction.

（强）连通分支的无圈序•acyclic ordering

label

such that there is no arc from

to

unless

t;jt;j . (initial, terminal, intermediate strong components of

.

事实： 一个连通图不是强连通的可以对其强连通分支进行无圈排序

2.2 特殊图类 （第二节）

Complete (di)graph G：

acomplete graphis a simpleundirected graph in which every pair of distinct vertices is connected by a uniqueedge. A complete digraph is a directed graph in which every pair of distinct vertices is connected by a pair of unique edges (one in each direction)

后续补充