java中开根号是什么函数_如何准确获取三角函数值？

点击上方蓝字了解更多精彩

作者简介：颜克清，毕业于长安大学数学专业，硕士。从教四年，安康市高新中学社团“数学思维培养中心”教师之一，在2017年全国中学生数学能力竞赛中，指导的学生成绩优异；在2018~2019学年党员优质课大赛中荣获三等奖；工作严谨扎实，多次荣获“优秀党员”称号。

对于后进生来说，初学高中数学必修四，认为该章内容晦涩难懂。尤其反应在三角函数值和三角函数恒等变形公式要记忆的东西多，容易忘，不能活用公式等问题。要解决这些问题，准确计算出某个角的三角函数值就尤为重要。首先我们要深刻理解三角函数的一些理论知识，包括其中的概念的深透理解和公式的熟练记忆。部分同学，开始学习三角函数定义时，没有理解其高中阶段的三角函数定义与初中的依托于直角三角形的三角函数定义的兼容性。这些孩子，有些对于初中的三角函数定义不了解或者不懂其意义。这些基础都会影响新概念的生成。所以新课时，我先引导学生回顾和理解初中的三角函数定义、初中所学的特殊三角函数值。打好概念的基础这节课后，对于三角恒等变形公式、三角函数的图像及性质的学习也有了很好的铺垫。

掌握获取三角函数值的运算程序，才能准确的，迅速的，合理的获得三角函数值。步骤是：遇到负角三角函数，转化为终边相同的角θ，θ∈(0,2π)，再转化为(0，π/2)内的三角函数值，最后计算出三角函数值。这样清楚每一步该做什么，就有章可循，避免乱猜乱碰绕弯子，影响运算速度。

引导学生总结反思，首先是针对初中的特殊三角函数值及意义，总结记忆口诀，以防紧急情况下出错。比如口诀：“一二三三二一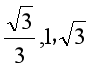，”，这里的“一二三三二一”，指的是前两行的分子中根号下的部分，所以一定也给学生阐述清楚，二分之根号下的“一二三三二一”，口诀顺口，记忆也迅速。

其次，根据单位圆下刻画的三角函数的定义，对照单位元中角度终边的对称性，计算出其他三个象限特殊的三角函数值，并分析各个现象三角函数值的正负号，以保证在后期运算三角函数值时，符号的正确性，对四个象限的特殊三角函数值要求理解记忆其符号和值。

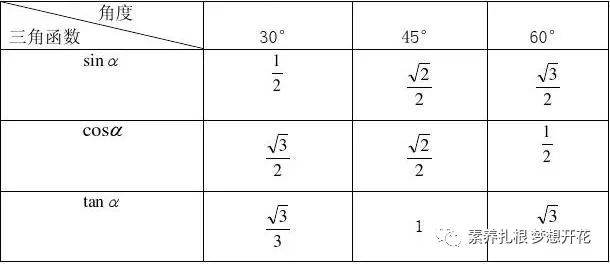
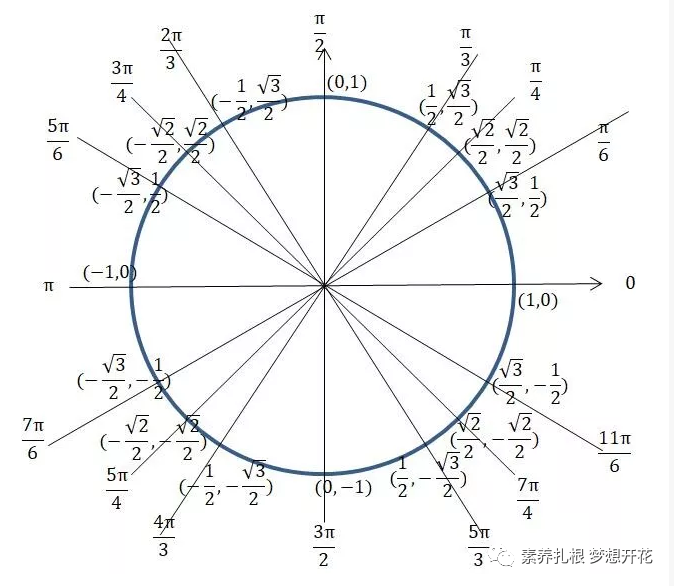
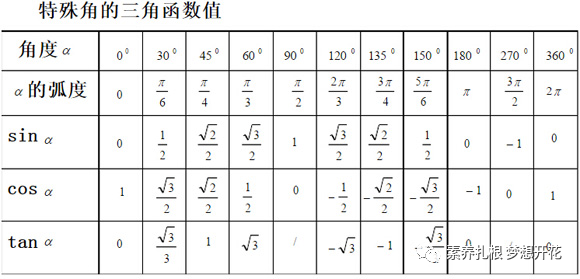
在这些学习和运算过程中，对后面学习的三角函数诱导公式有极其重要的作用，观察、理解特殊角度终边的对称性，结合三角函数值定义，确定了其函数值之间的关系。

结语：对于后进生来说，基础理论相关的运算尤为重要，对后期进一步的知识深化，有不可或缺的重要性。所以我在教学中，一直都非常重视开始知识生成阶段里学生相关的运算能力，理解透彻概念、定义、公式后，加强运算能力的训练，运算的正确也提高了学生的学习兴趣和信心，在这种知识探究和运算的过程中，也拔高了学习能力，这些与高中数学中的逻辑思维能力，分析问题解决问题能力也都息息相关，有助于学生整体数学素养的慢慢提升.