lasso回归_正则化是什么？以及Ridge和 Lasso回归的区别

之前在其他文章上看到Ridge和Lasso回归分别代表L1和L2的正则化，L1会把系数压缩到0，而L2则不会，同时L1还有挑选特征的作用，网上写的总结知识文章写的特别好，但没有一直没有形象化的认识，今天就用代码例子来看看区别，顺便梳理一下正则化的知识。

首先我们要明确正则化的作用：防止过拟合！预防过拟合！

那么正则化是怎么样是的模型不倾向于过拟合呢？

通过缩减系数项使得模型对于自变量的敏感程度降低，进一步降低模型的整体方差.（Variance）

我们可以画一个图来帮助理解：

对于上图的黄线，每增加一单位的X，Y就会响应的增加2倍

而对于绿线和蓝线来说，每增加以单位的X，Y的增加量被压缩了，这就是正则项在做的事：让预测值对于单一自变量X的敏感程度降低，具体降低的程度取决于我们的正则化力度，方式。

说完总体概念，我们通过一个例子来理解一下Ridge回归的作用

首先我们假设有如下样本响应分布：

在没有正则化，仅仅依靠最小化均方误差，我们可以得到下图中的拟合曲线：

看上去很美好对不对？接下来我们考虑一个特殊情况，如果我们的训练集就只有2个训练点呢？如果只有两个训练点，我们依靠最小均方误差，得到的将会是如下这个曲线：

不用想也知道，模型过拟合了，虽然他完美的拟合了给定了2个训练集数据，但是对于总体样本来说，拟合效果是非常差的。

接下来我们引入岭回归（Ridge Regression），这样模型的目标函数除了经验风险最小化，额外引入了结构风险最小化的部分，也就是额外引入了下式引号的右半部分：

下图中，红色的点是我们的训练集，绿点是其他样本分布，蓝线是原始你和曲线，可以清晰的看到，引入了正则项后，模型的效果好了很多，除了截距基本和原始曲线拟合效果差不多了！

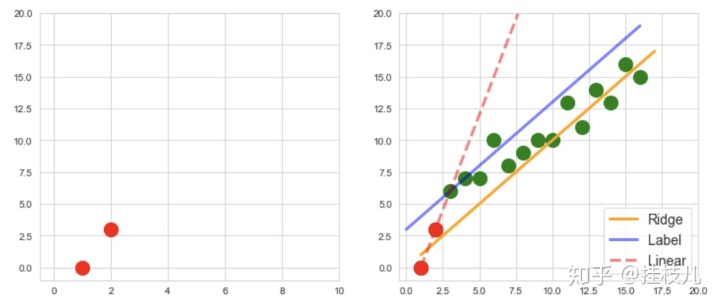
此处重新再写一遍加深印象： 正则化的目的在于让预测值对于单一自变量X的敏感程度降低，具体降低的程度取决于我们的正则化力度，方式。

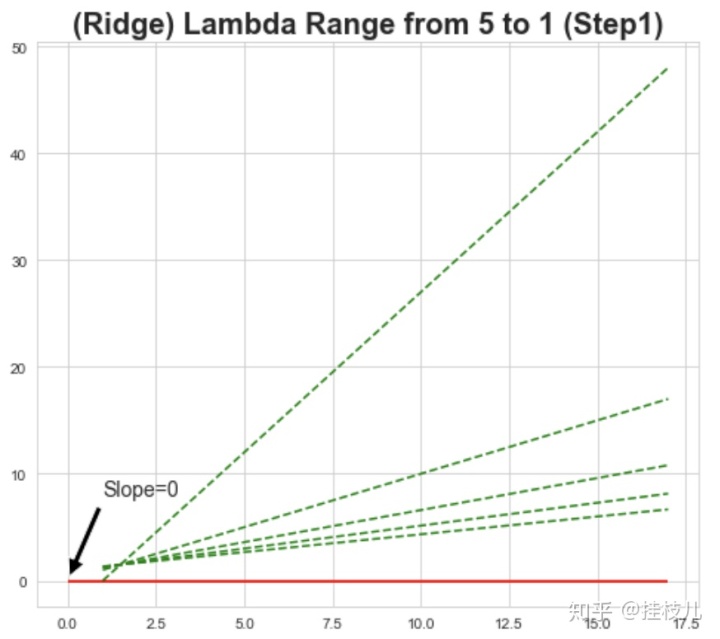
那么我们见识到了正则化的力度，接下来我们看看不同的正则化力度，对于模型的拟合曲线会有什么样的影响：

我们观察下图可以看到：

以1作为步长，在惩罚力度等差增大时，惩罚力度是在逐渐减小的， 也就是说随着惩罚力度的增加，惩罚的效果会逐步减小（但注意拟合函数没有真的变成0）

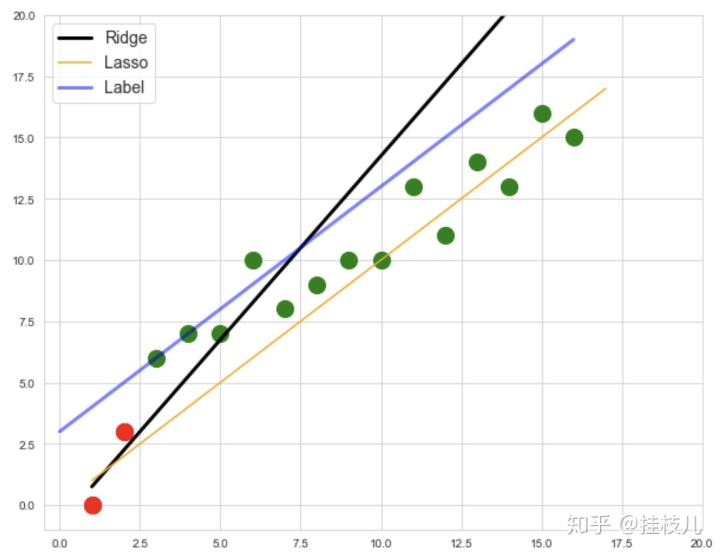
接下来我们再看看LASSO回归，还是用上面那个2个红点作为训练集，我们来看看LASSO和Ridge在同样惩罚力度下的效果，LASSO的公式是：

可以看到和Ridge一样，LASSO的也进一步降低了模型自变量对于2个训练集标签的敏感性。

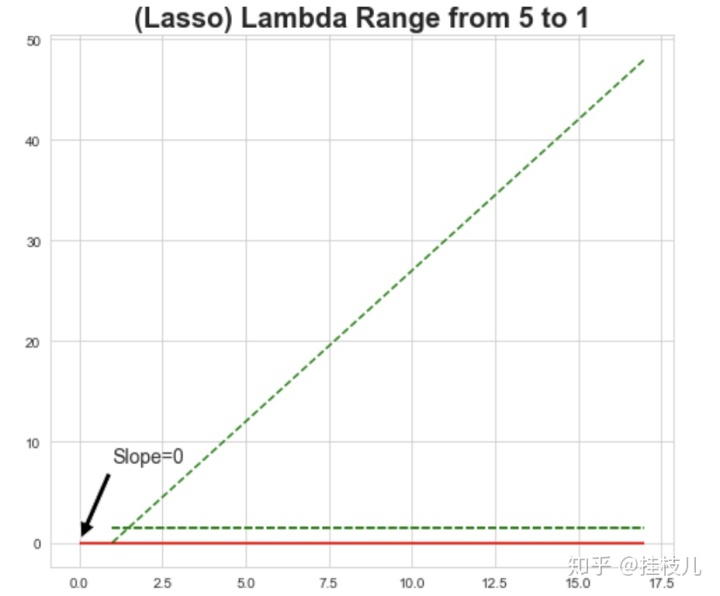
再来画一下LASSO惩罚力度逐步增大对于拟合曲线的改变：

可以看到LASSO非常社会，第二个步长就把系数压缩到了0.

这里我贴一个我觉得这种变化解释的非常好的答案：

l1正则与l2正则的特点是什么，各有什么优势？​www.zhihu.com

答主是通过2种类型的正则化的导出角度解释区别的：

Lasso回归正则化，在梯度下降时求得的梯度始只有1和-1两种值，所以每次更新步长它都在稳步向前前进

Ridge回归的正则化的梯度会随着临近最低点而减小，在接近最小值的时候其梯度也会变小，所以不会真的变成0.

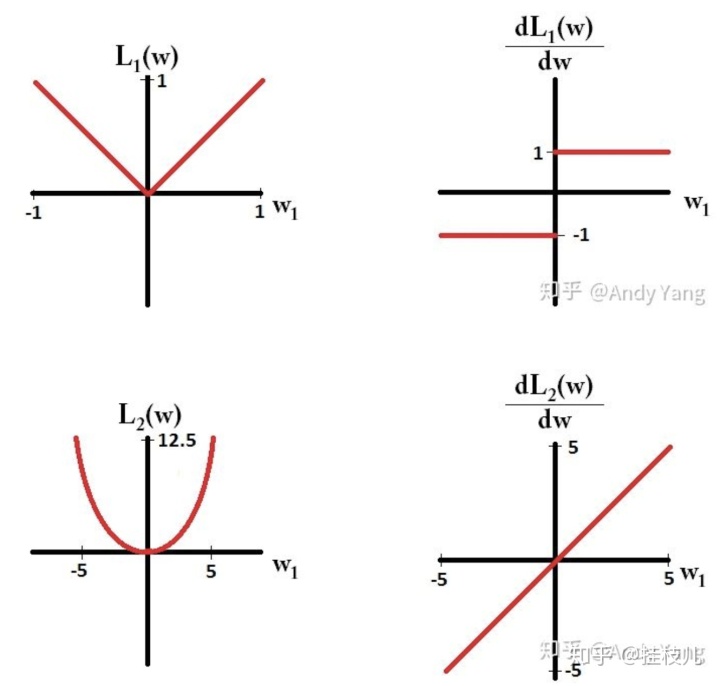
最后还有一个关于Lasso回归等式的稀疏性，和可以用来挑选特征2个特性，我目前的知识储备感觉这两个是一回事：使回归式中与相应变量无关系的的变量系数为0。

我在下面画了个例子，自带2个特征，20个噪声特征，选一个比较大的惩罚系数：

from 

接下来拟合曲线：

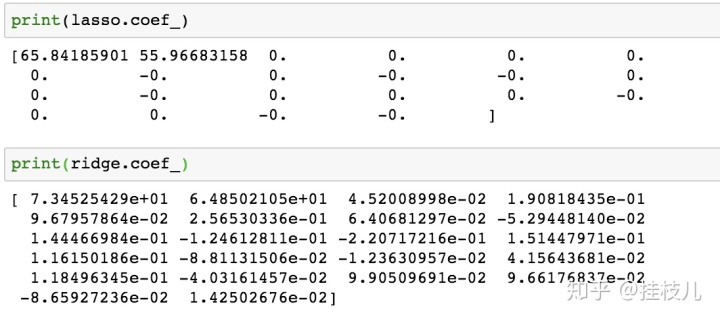
lasso 

我们把2个式子的系数打出来看看：可以看到l1把噪声特征都压缩成了0，而l2啧对于噪声特征赋予了一个非常低的权重。对此我其实有一个小疑问：实务中都开始做模型了难道不提前调好变量吗哈哈