贝叶斯定理 php,Spark mllib 贝叶斯分类

贝叶斯定理

已知某条件概率，如何得到两个事件交换后的概率，也就是在已知P(A|B)的情况下如何求得P(B|A)。这里先解释什么是条件概率：

表示事件B已经发生的前提下，事件A发生的概率，叫做事件B发生下事件A的条件概率。其基本求解公式为：

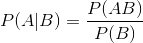
贝叶斯定理之所以有用，是因为我们在生活中经常遇到这种情况：我们可以很容易直接得出P(A|B)，P(B|A)则很难直接得出，但我们更关心P(B|A)，贝叶斯定理就为我们打通从P(A|B)获得P(B|A)的道路。

下面直接给出贝叶斯定理：

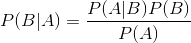package com.immooc.spark

import org.apache.log4j.{Level, Logger}

import org.apache.spark.mllib.classification.NaiveBayes

import org.apache.spark.mllib.linalg.Vectors

import org.apache.spark.mllib.regression.LabeledPoint

import org.apache.spark.{SparkConf, SparkContext}

object NaiveBayesTest {

def main(args:Array[String]): Unit = {

val conf = new SparkConf().setAppName("NaiveBayes").setMaster("local[2]")

val sc = new SparkContext(conf)

Logger.getRootLogger.setLevel(Level.WARN)

val data = sc.textFile("file:///Users/walle/Documents/D3/sparkmlib/football.txt")

val parsedData = data.map{ line =>

val parts = line.split(',')

LabeledPoint(parts(0).toDouble, Vectors.dense(parts(1).split(' ').map(_.toDouble)))

}

val splits = parsedData.randomSplit(Array(0.6, 0.4), seed = 11L)

val training = splits(0)

val test = splits(1)

val model = NaiveBayes.train(training, lambda = 1.0, modelType = "multinomial")

val predictionAndLabel = test.map(p => (model.predict(p.features), p.label))

val print_predict = predictionAndLabel.take(20)

for (i

println(print_predict(i)._1 + "\t" + print_predict(i)._2)

}

println("Predictionof (0.0, 2.0, 0.0, 1.0):"+model.predict(Vectors.dense(0.0,2.0,0.0,1.0)))

}

}

1. 数据0,0 0 0 0

0,0 0 0 1

1,1 0 0 0

1,2 1 0 0

1,2 2 1 0

0,2 2 1 1

1,1 2 1 1

0,0 1 0 0

1,0 2 1 0

1,2 1 1 0

1,0 1 1 1

1,1 1 0 1

1,1 0 1 0

0,2 1 0 1

2. 输出1.01.0

1.01.0

0.01.0

1.01.0

0.00.0

Predictionof (0.0, 2.0, 0.0, 1.0):0.0

Post Views: 3

Related Posts 4671