java扫雷代码简单实现_数值微分的简单代码实现

数值微分是数值方法中的名词，它可以根据函数在一些离散点的函数值，从而推算出它在某点的导数的近似值。在平常写代码的过程中，经常会调用某些优化算法比如随机梯度下降算法等，因为

、

等深度学习算法库都已经封装好了相关算法，直接调用

即可得到相应结果，所以很自然的会忽略梯度的底层实现。带着这个疑惑我查阅了很多文献资料，阅读下来发现这些算法库自动计算梯度的理论还蛮复杂的，但是实现一个简单的数值微分算法还是挺简单的，具备中学数学知识即可！本文的pdf版本已上传至Github，如果有需要可以自行下载。

如果你觉得有帮助的话，欢迎点个赞，比心 ！

1 一元函数的数值微分

可以根据函数在某点处导数的定义来实现代码，首先回顾一下函数在一点处导数的相关定义

定义 设函数

在点

的某个邻域内有定义，当自变量

在

处取得增量

(

仍在该邻域内)时，相应地，因变量取得增量

；如果

与

之比当

时极限存在，那么称函数

在点

处可导，并称这个极限为函数

在点

处地导数，记为

，即

也可记作

或

。

由于计算机计算数值微分会带来误差，故对原始定义做一个调整

使用调整后的导数定义求解数值微分要比单边近似地精度要高，有了理论基础就可以使用代码实现

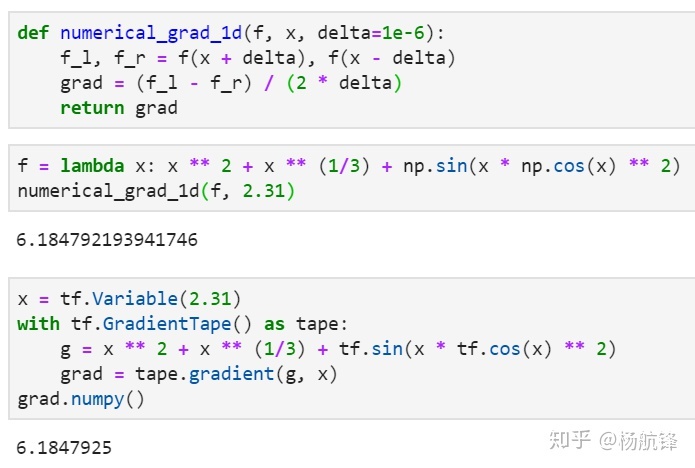
def 

例如使用上述代码计算函数

在

处地导数值

import 

通过

自动微分可以验证计算地准确性

import 

两者计算结果对比

2 多元函数的数值微分

同理可以根据多元函数偏导数的定义来实现代码，多元函数在某一点处偏导数的定义如下

定义 设函数

在点

的某一邻域内有定义，若

存在，则称此极限为

函数在点

处对

的偏导数，记作

即

同样的，若

存在，则称此极限为

函数在点

处对

的偏导数，记作

即

为了减小单边计算误差，对原始定义也做一些微调

多元函数的数值微分代码实现

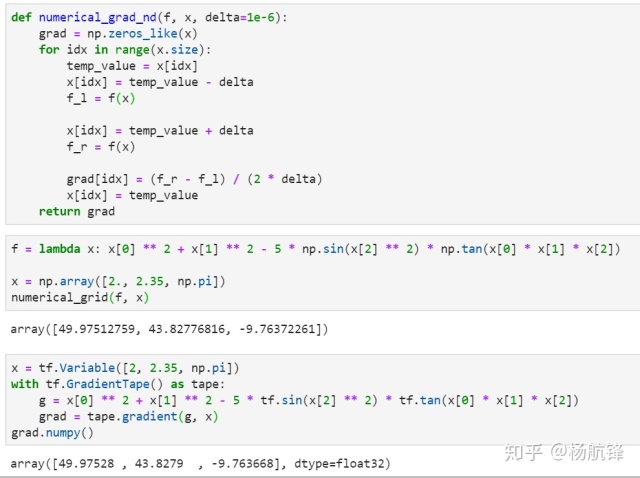
def 

例如使用上述代码计算多元函数

在点

处的梯度值

f 

通过

自动微分可以验证计算地准确性

x 

两者计算结果对比