n型半导体和p型半导体的区别_电子学笔记——半导体物理基础（三）

目录

第一章 绪论

1.1 半导体性质概览

1.2 半导体材料

1.3 半导体元件

第二章 能带结构

2.1 定性

2.2 自由电子模型

2.3 周期晶格中的自由电子

2.4 带隙

2.5 有效质量

2.6 状态密度（本次笔记结束之处）

第三章 电荷载体统计

3.1 Fermi分布

3.2 本征半导体

3.3 掺杂半导体

3.4 多数载流子与少数载流子（本次笔记结束之处）

第四章 电子载体的运动

4.1 Bloch电子的运动

4.2 电子载体的漂移

4.3 电子载体的扩散

第五章 pn结

5.1 热力学平衡

5.2 耗尽层

5.3 耗尽层电容

5.4 IU特性曲线

5.5 二极管简介

---

第三章 电子载流体统计学

3.1 Fermi统计

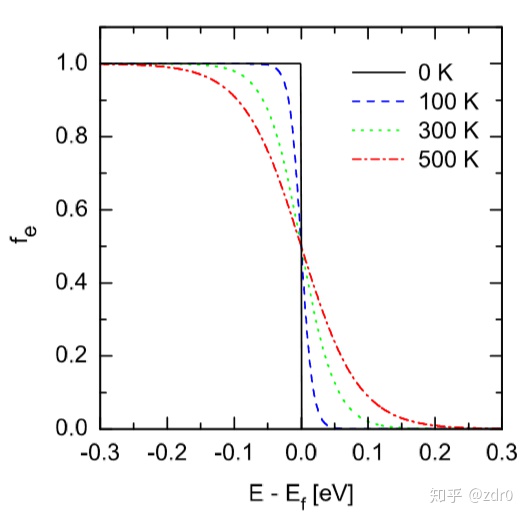
Fermi-Dirac分布

其中：

：

Boltzmann常数；

：

Fermi能，目前还不确定，但其在带隙中的任何位置。

图片3.1：Fermi-Dirac分布曲线。

3.2 本征半导体

本征态：

没有掺杂原子；

没有杂质原子；

没有光激发，等等...

3.2.1 有效状态密度

在整个导带中有多少电子？首先我们需要考察的是状态密度：

则导带中的电子数目

为：

但这个积分过于复杂，因此我们需要化简一下：

• 非退化系统；
• Fermi能在带隙的深处；
• Fermi-Dirac分布近似为Maxwell-Boltzmann分布；
• 结论：有效状态密度：

意义：

• 能带中的所有“可用的”状态总和；
• 注意：只在非退化系统中；
• 与温度
  有关；
• 电子载流体密度的简便计算：

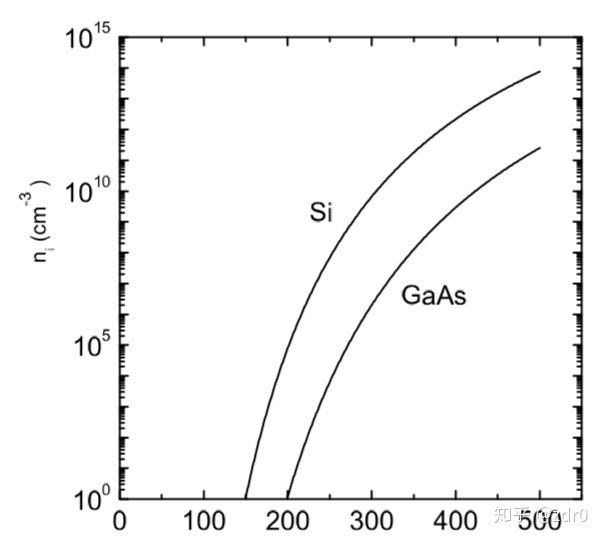
本征电子载流体密度：

• ；
• 且
  ；
• 关于
  成指数增长；

图片3.2：Si，Ge本征态下的电子载流体密度n_i与温度之间的关系。

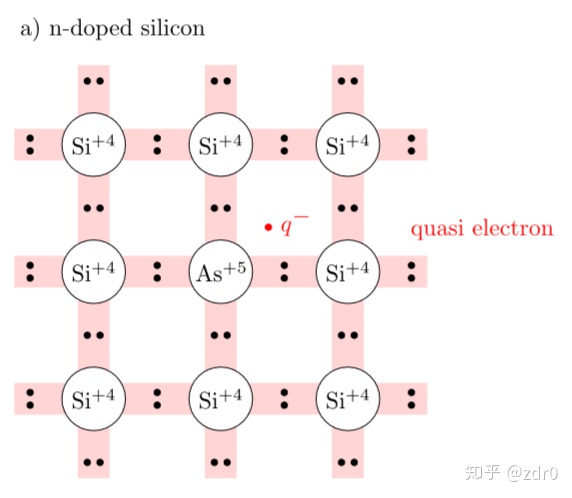
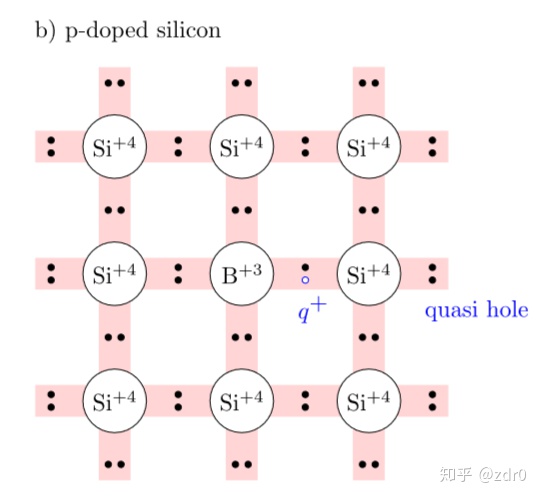
3.3 掺杂半导体

掺杂：

一般来讲是晶体中的原子被外来原子所替换；

• ：
  型掺杂原子的密度（
  施主原子）
• ：
  型掺杂原子的密度（
  受主原子）

图片3.3：Si晶体中掺杂施主原子As（n掺杂），导致晶体中的自由电子数目增加。

图片3.4：Si晶体中掺杂施主原子B（p掺杂），导致晶体中的空穴数目增加。

图片3.5：n掺杂的半导体的能带。

图片3.6：p掺杂的半导体的能带。

质量作用定理

• 仅适用于平衡条件下（没有电流）；
• 电荷和空穴的浓度：
  ；
• 本征密度：

图片3.7：n掺杂半导体（i）能带；（ii）状态密度；（iii）Fermi分布；（iv）n，p的密度。

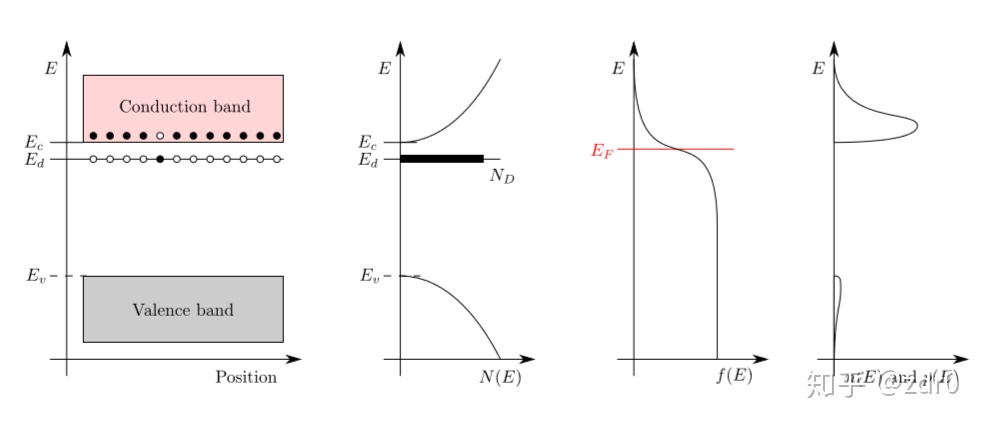
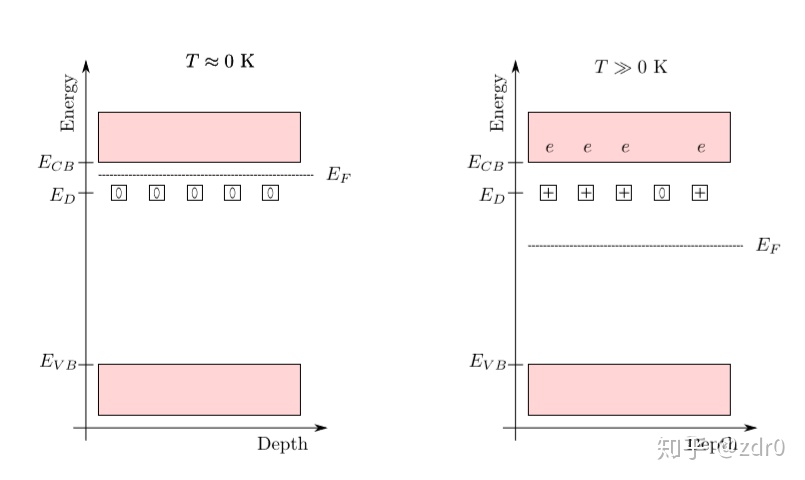
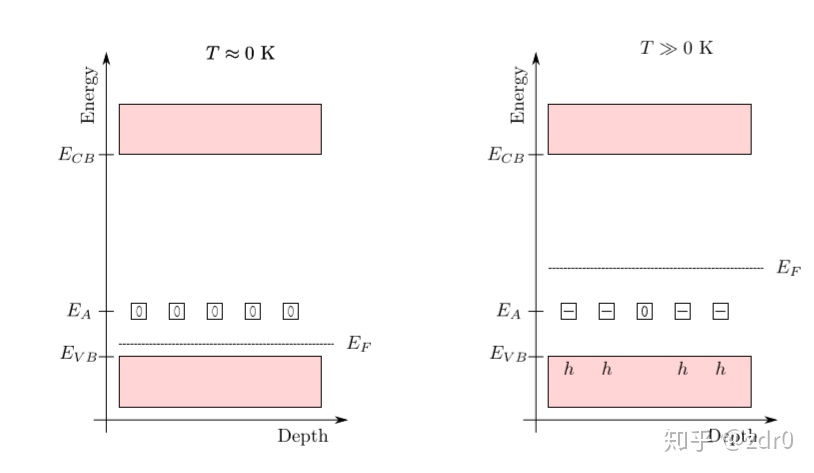
临时假设：掺杂原子的能量与能带边界的能量仅有少量差距

• 施主原子：
• 受主原子：

完全电离状态下的n的密度：

利用有效状态密度

：

则得到n掺杂半导体中的Fermi能为：

完全电离状态下的n的密度：

利用有效状态密度

：

则得到n掺杂半导体中的Fermi能为：

完全电离状态下的p的密度：

利用有效状态密度

：

则得到n掺杂半导体中的Fermi能为：

3.4 多数载流子和少数载流子

多数载流子：

• ：n掺杂半导体中的电子；
• ：p掺杂半导体中的空穴。

少数载流子：

• ：p掺杂半导体中的电子；
• ：n掺杂半导体中的空穴。

电中性条件和质量作用原理：

完全电离状态下的电中性条件：

平衡状态下的质量作用原理：

从而对于n掺杂半导体有：

对于p掺杂半导体有：

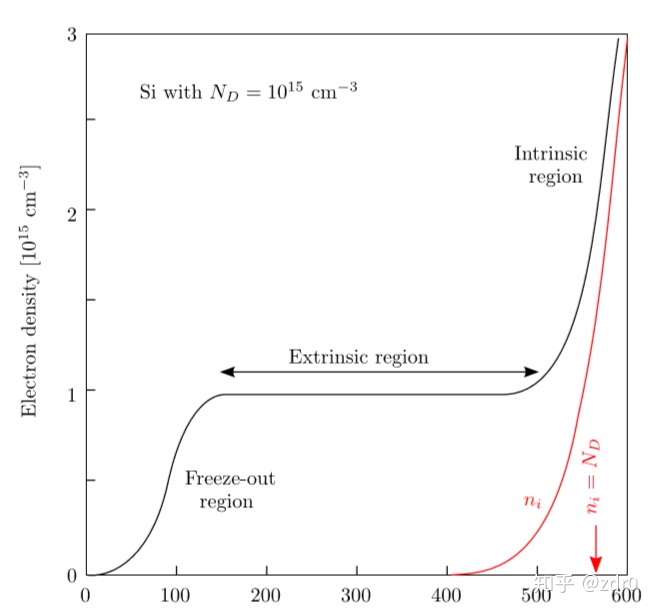
3.4.1 温度影响

• 低温状况下掺杂原子没有被电离；
• 高温状态下本征载流子的浓度成指数增长。

图片3.18

---