移位操作 浮点数_浮点数处理

> 由于知乎编辑器对markdown支持性问题，本文为直接上传markdown文档，格式混乱且图像不全，格式完整版请移步个人博客

浮点数处理​qiankun214.github.io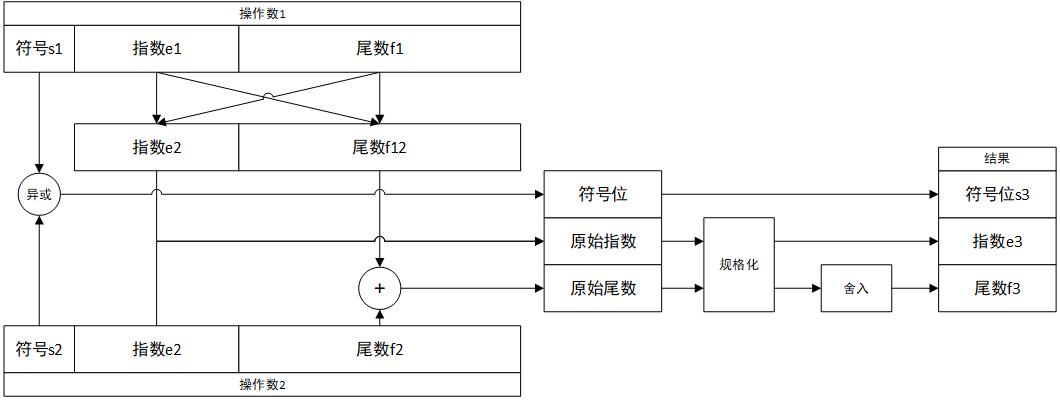

浮点数表达

IEEE754标准是用于规范浮点数运算的IEEE标准，用于解决浮点数标准混乱的问题。其被认证后不久，几乎所有的处理器生产商都采用这一标准，极大的推动了软件的发展。浮点数存储的格式如下：

浮点数由符号位，指数位和尾数三个部分组成，表达公式如下式： $$ X = (-1)^{s} times f times 2^{e} $$ 在IEEE754标准中，主要规定了单精度浮点（float）和双精度浮点（double）两种浮点数：

| 类型 | 符号位数 | 指数位数 | 尾数位数 | | -------------------- | -------- | -------- | -------- | | 单精度浮点（float） | 1 | 8 | 23 | | 双精度浮点（double） | 1 | 11 | 52 |

首先考虑符号位，当该符号位为0时，表示该数为正数，符号位为1时，表示该数为负数。指数可以为负数，一般使用移码表示，移码表示为： $$ E = e- bias $$ E为真实的指数，e为浮点数中存储的尾数，bias为移位，有$bias = 2^{len(e) - 1} - 1$。以单精度浮点为例，指数位数$len(e) = 8$，则有bias=127，真实指数和存储的关系为$E = e - 127$，表示范围为-126~127（e=0和e=255用于表示特殊字符）。尾数为规格化的尾数，即尾数的二进制表示$f_b$前有一个隐藏的二进制1，即如下表示： $$ X = (-1)^{s} times 1.f_b times 2^{e-bias} $$ 当e=0时，该浮点数为非规格化数，表示的数如下所示： $$ X = (-1)^s times 0.f_b times 2^{-126} $$ 该标准内还定义了几个特殊值：

| 特殊值 | 说明 | | ------ | ------------------------------------------------------- | | 0 | 指数部分和尾数部分均为1 | | 无穷大 | 指数部分为$2^{len(e)} - 1$（指数最大值），尾数部分为0 | | NaN | 指数部分为$2^{len(e)} - 1$（指数最大值），尾数部分不为0 |

浮点数计算

浮点数乘法

浮点数的乘法分为以下几个步骤：

• 计算符号位：通过异或操作计算符号位，若两个操作数符号位相同，则结果符号位为0，否则结果符号为1
• 计算原始尾数：两个操作数的尾数相乘，得到原始尾数
• 计算原始指数：将两个操作数的指数相加，得到原始指数
• 规格化与舍入：对原始尾数和原始指数进行规格化，获得结果的指数，再对尾数进行舍入，获得结果的尾数

对于科学计数法表示的乘法，有： $$ [(-1)^{s_1} times 1.f_1 times 2^{e_1}] times [(-1)^{s_2} times 1.f_2 times 2^{e_2}] = (-1)^{s_1 XOR s_2} times (1.f_1times 1.f_2) times 2^{e_1+e_2} $$ 现考虑32位的单精度浮点数（float），其指数为8位，尾数为23位，获得原始指数和原始尾数为：

• 原始指数：原始指数为两个8位的指数相加，共9位
• 原始尾数：原始尾数为两个23位的尾数相乘，共46位

获得原始指数和尾数后进行规格化，若原始指数小于-126，则小于表示范围，将原始尾数右移，每右移一位，原始指数+1，直到原始指数到达-126，此时形成非规格化数。若原始尾数不小于-126，进行正常的标准化：

• 两个规格化数相乘：$1.f_1 times 1.f_2$，结果在1~4之间，即最高2位有以下几种可能性：
• 最高2位为01：原始尾数向左移位2位（包括移除隐含的1），原始指数直接为获得规格化的指数，小数部分还剩44位，在舍入部分处理。若原始指数-2后为-127，则在移位后尾数前添加1，使用非规格化表示
• 最高2位为10或11：原始尾数向左移位1位（移除隐含的1），原始指数+1获得规格化的指数，小数部分还剩45位，在舍入部分处理。
• 非规格数和规格化相乘：$1.f_1 times 0.f_2$，结果在0~2之间，操作方式与上述类似
• 非规格化数和非规格化数相乘：原始指数为-252，尾数部分仅有46位，无论如何都不可能使指数规格化到-126，直接为0

进行规格化后，原始指数被修正为指数$e_3$，此时若尾数的位数超过23位，还需要进行舍入操作。将规格化后的尾数使用$sf$表示，$sf[h:h-23]$表示高23位的指数，$sf[h-24:0]$表示24位以后尾数。舍入使用“四舍六入”的方式，舍入规则如下所示：

• 若$sf[h-24:0] < 1000...0$：抛弃，舍入结果为$sf[h:h-23]$（四舍）
• 若$sf[h-24:0] > 1000...0$：进位，舍入结果为$sf[h:h-23]+1$（六入）
• 若$sf[h-24:0] == 1000...0$：舍向偶数，即使$sf[h:h-23]$变为偶数（$sf[h:h-23]$为奇数时进位，否则抛弃）

进行舍入后，原始尾数被修正为尾数$f_3$，乘法计算完成。

浮点数加法

浮点数的加法分为以下几个步骤：

• 对阶：将指数较小的浮点数进行尾数向右移位，指数同步增大，直到两个操作数的指数等
• 求和：对尾数进行求和
• 规格化：对指数和尾数做规格化，并对尾数进行舍入

对于科学计数法表示的加法，有： $$ [(-1)^{s_1} times 1.f_1 times 2^{e_1}] + [(-1)^{shttps://qiankun214.github.io/2019/05/28/%E6%B5%AE%E7%82%B9%E6%95%B0%E5%A4%84%E7%90%86/_2} times 1.f_2 times 2^{e_2}] = [(-1)^{s_1} times 1.f_1 times 2^{e_1-e_2}+ (-1)^{s_2} times 1.f_2] times 2^{e_2} $$ 第一步为对阶，即将指数变为相同以实现加法，规定小阶向大阶对阶，即原始指数$e=max{e_1,e_2}$，对于指数较小的操作数，需要将尾数向右移位，每移动一位，指数加1，移位直到阶数相等即完成对阶，对阶过程可表示为： $$ begin{cases}(-1)^{s_1} times 1.f_1 times 2^{e_1} (-1)^{s_2} times 1.f_2 times 2^{e_2}end{cases} to begin{cases}[(-1)^{s_1} times 1.f_1 times 2^{e_1 - max{e_1,e_2}}] times 2^{max{e_1,e_2}} [(-1)^{s_2} times 1.f_2 times 2^{e_2 - max{e_1,e_2}}] times 2^{max{e_1,e_2}}end{cases} $$ 第二步为求和，即对阶完成后，两个尾数可以直接求和获得原始尾数，求和过程如下所示： $$ begin{cases}[(-1)^{s_1} times 1.f_1 times 2^{e_1 - max{e_1,e_2}}] times 2^{max{e_1,e_2}} [(-1)^{s_2} times 1.f_2 times 2^{e_2 - max{e_1,e_2}}] times 2^{max{e_1,e_2}}end{cases} to [(-1)^{s_1} times 1.f_1 times 2^{e_1 - max{e_1,e_2}} + (-1)^{s_2} times 1.f_2 times 2^{e_2 - max{e_1,e_2}}] times 2^{max{e_1,e_2}} $$ 第三步为规格化和舍入，原始尾数$f = (-1)^{s_1} times 1.f_1 times 2^{e_1 - max{e_1,e_2}} + (-1)^{s_2} times 1.f_2 times 2^{e_2 - max{e_1,e_2}}$，原始指数$e=max{e_1,e_2}$，对其进行规格化和舍入操作，获得新的指数$e_3$和尾数$f_3$，操作方式与乘法相同，即完成浮点数的加法。