世界坐标系到观察坐标系的变换步骤_《3D数学基础》提炼总结（九）矩阵和线性变换...

一、变换物体与变换坐标系

在讨论变换前，必须要搞清楚到底要变换什么。

考虑2D中的例子“将以物体顺时针旋转20度”。变换物体（本例中为旋转），以为这旋转物体上所有的点，这些点将被移动到一个新的位置。我们使用同一坐标系来描述变换前和变换后点的位置。

现在，和变换坐标系的概念进行比较。旋转坐标系时，物体上的点实际没有移动，我们只是在另一个坐标系中描述它的位置而已。

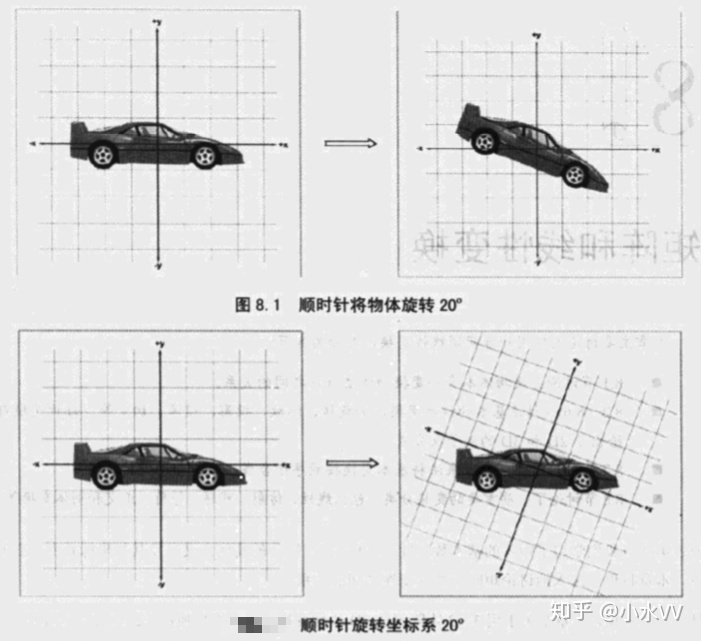
我们将证明这两种变换在某种意义上是等价的，但现在，先看看它们各自的优点

变换物体的用处非常明显。例如，为了渲染一辆车，必须将点从车的物体坐标系变换到世界坐标系，接着到摄像机坐标系。那么为什么还要变换坐标系呢？乍看起来，把坐标系旋转到这个奇怪的位置似乎并没有什么价值。观察下图就可以发现，其实旋转坐标系就能起到很好的作用。

下图展示了一把步枪，正在向汽车发射子弹，如左边的图所示，我们一开始就知道世界坐标系中枪的位置和子弹的弹道。现在，想象一下世界坐标系被旋转到和车的物体坐标系重合的位置，而与此同时保持车、枪、子弹弹道不动。这样，我们得到了枪和子弹弹道在车的物体坐标系中的坐标，接着可以作碰撞检测以检查子弹是否会击中汽车了。

当然，也可以将车旋转到世界坐标系，在世界坐标系中作碰撞检测，但这要花费更多的时间，因为车的模型可能有大量的顶点和三角形，计算量太大。现在，不必担心实际变换的细节问题，这正是本章的剩余部分要对付的。只需记住可以变换问题，也可以变换坐标系。某些情况下一种方法比另一种更合适。

对于两种变换保持一种概念上的区别还是有必要的，有些情况下需要进行物体变换，另外一些情况下则需要进行坐标系变换。然而，这种变换实际上是等价的，将物体变换一个量等价于将坐标系变换一个相反的量。

二、旋转

1.2D中的旋转

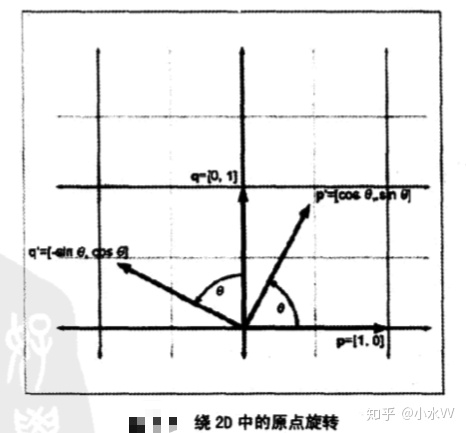
在2D环境中，物体只能绕某个点旋转，因为现在暂不考虑平移，这里我们进一步限制物体，使其只绕原点旋转。2D中绕原点的旋转只有一个参数：角度

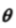
，它描述了旋转量。逆时针旋转经常（不是必须）被认为是正方向，顺时针方向是负方向。下图展示了基向量 p,q绕原点旋转，得到新的基向量

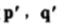
现在我们知道了旋转后基向量的值，就可以以公式的形式构造矩阵如下。

2.3D中绕坐标轴的旋转

在3D场景中，绕轴旋转而不是点（此时，轴指的是旋转所绕的直线，不一定是笛卡尔坐标轴x,y或z).再次声明，这里暂不考虑平移，所以只讨论旋转轴穿过原点的情况。

绕轴旋转

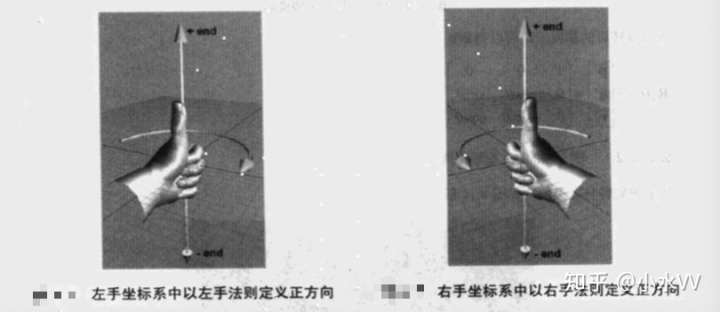
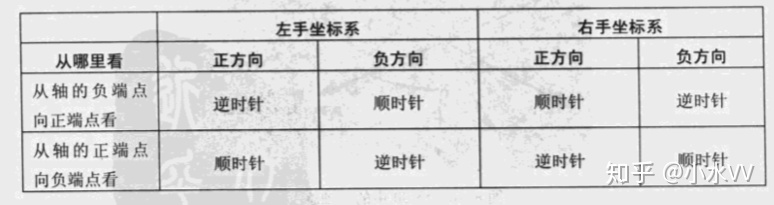
时，必须知道哪个方向被认为“正”，哪个方向被认为“负”，左手坐标系中定义此方向的规则为左手法则。首先，要明确旋转轴指向哪个方向。当然，旋转轴在理论上是无限延伸的，但我们还是要认为它有正端点和负端点。与笛卡尔坐标轴定义坐标系相同，左手法则是这样的：伸出左手，大拇指向上，其余四指弯曲。大拇指指向旋转轴的正方向，此时，四指弯曲的方向就是旋转的正方向。此时，四指弯曲的方向就是旋转的正方向，此时，四指弯曲的方向就是旋转的正方向。如下图所示。

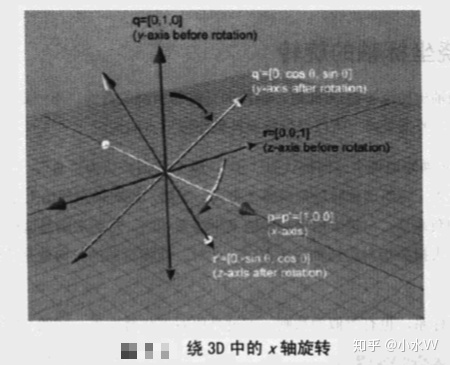
最为常见的旋转是绕某坐标轴的简单旋转。让我们从绕x 轴旋转开始。

求出旋转后的基向量，可以得到矩阵。

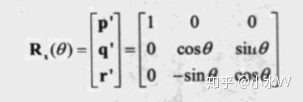
与绕y轴的3D旋转与之类似，如图

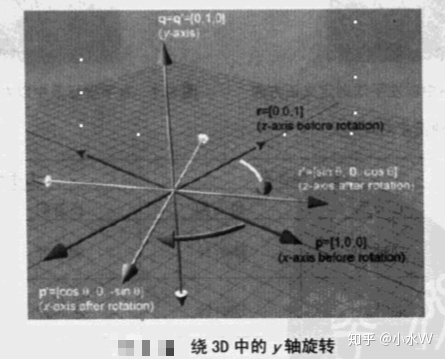
可得绕y轴旋转的矩阵。

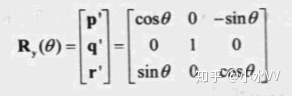
最后是绕z轴的旋转如公式所示

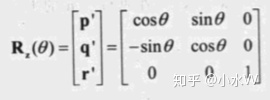
3.3D中绕坐标轴的旋转

当然也能绕3D中的任意轴旋转。因为这里不考虑平移，可以假设旋转轴通过原点。这种旋转比绕坐标轴的旋转更复杂也更少见。用单位向量n描述旋转轴，和前面一样用

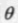
描述旋转量。

v'是向量v绕轴n旋转后的向量。让我们看看能否用v,n和

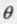
表示v‘。我们的想法是在垂直于n的平面中解决这个问题，那么这就转换为了一个简单的2D问题。为了做到这一点，将v分解为两个分量：

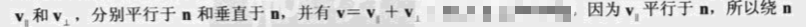
-------------------------------------------------------------------------------------------暂时发布还没有写完