matlab对数组求和很多元素_简谈matlab的dot命令-优快云博客

本文介绍了MATLAB中的dot命令用于计算向量或矩阵内积的基本用法。当应用于2维矩阵时，dot命令默认按列计算内积，而通过指定参数dim可以改变这一行为，例如dim=1表示按列计算，dim=2表示按行计算。对于高维矩阵，dot命令以指定维度为单位进行内积运算。文中给出了具体的三维矩阵和四维矩阵的示例，并提供了测试代码供读者验证理解。

在matlab中,dot命令是计算向量或矩阵的内积,在矩阵论中,若a,b是向量,则内积使用表示,其本质是对应元素相乘后再将各项加在一起,即

=a1b1+a2b2+…+anbn

若A,B是2维矩阵,在使用dot计算内积时,matlab把A,B中各列看作向量,分别计算对应列的内积,也可以使用带参数dim的格式,即

dot(A,B,dim)

这个格式中,当dim=1时,以对应各列为基本向量,计算内积;当dim=2时,以对应各行为基本向量,计算内积;当dim=3时,此时矩阵属于高维矩阵,按照矩阵的维度由低到高,若设定为列、行、页、册、卷等逐级升高的维度代号,则当dim=3时,首先以页为操作单位,将对应页上对应位置的元素求积,再将各页上求得的积,按对应位置求和。

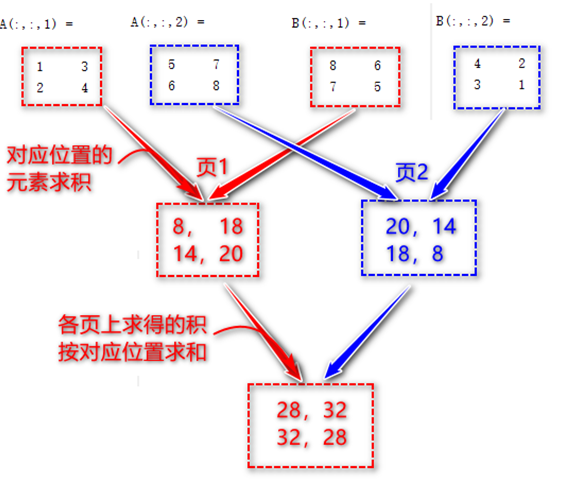
例如,三维矩阵A,B如下,

则dot(A,B,3)的计算如下:

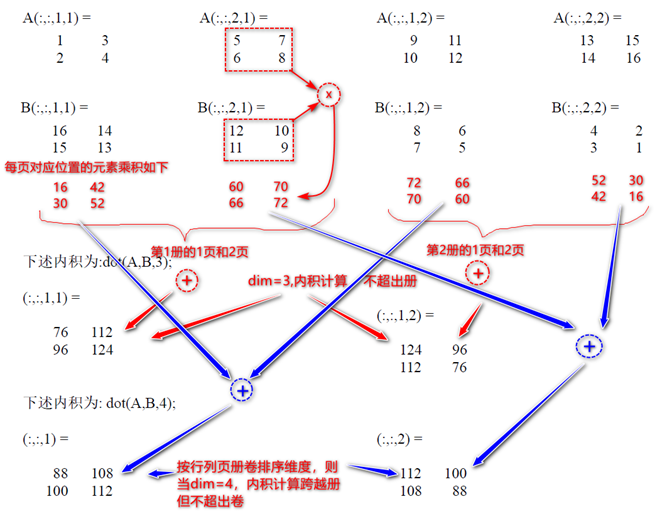
再举一个4维矩阵的例子，其具体计算如图。

为了方便验证，下面给出上述例子的实现代码，可自己运行测试，

function testFunc(n,k)% 功能：dot函数的高维数组测试函数% 参数：n—维数；k—维度量值;二者均为正整数。vec='[';for iLoop=1:n vec=horzcat(vec,'k ');endvec=horzcat(vec,']');vec=eval(vec);A=reshape(1:k^n,vec);B=reshape(k^n:-1:1,vec);for iDim=1:n fprintf('\n下述内积为: dot(A,B,%d);\n',iDim); disp(dot(A,B,iDim));end上述代码摘自《MATLAB语言编程》一书，更多细节，请参阅该书。