fft 相位谱_谈谈FFT到底有何用（谨以此献给致力于FFT算法芯片设计的同行们）...

FFT(快速傅里叶变换)是数字信号处理的超级经典算法，学过DSP或者芯片设计的人大多知道这个算法。但是，大家是否想过，为什么数字信号处理会有那么多FFT呢？有人会说，为了分析信号的频谱。那么下边的问题就是，分析频谱对我们的日常需求，比如手机打电话，雷达测量速度和方向等等一些与实际需求有什么联系？为什么FFT如此重要？本文举一些简明的例子，阐释一下FFT到底有什么用。

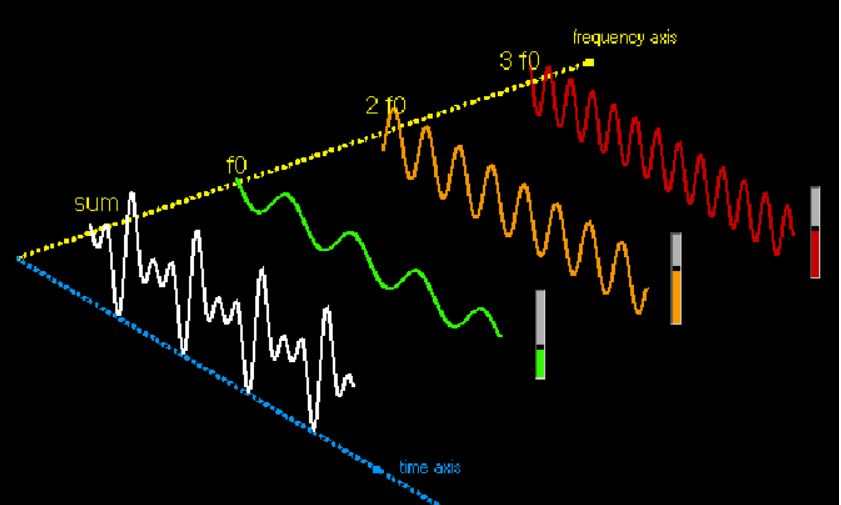
先回忆一下FFT是什么。上世纪70年代之前，我们主要通过模拟电路来进行信号处理，比如大家熟悉的用二极管和电容进行AM调制信号的包络检波一样，随着数字系统的普及，我们可以用处理器或者数字电路更为精确的处理信号，比如我们做AM检波，实际上可以用载波把信号混频(与余弦函数做乘法)，再进行低通滤波，那么这个过程可以用数字电路的乘法器和FIR滤波器来做，FIR比二极管和电容构成的低通滤波器阶数高的多，性能自然更为理想，同时，由于数字电路易于做成集成电路，因此我们更多地是将原先的模拟信号(比如麦克风的音频)通过模拟-数字转换器，转换为数字值后进行处理。

这样的系统有几个问题，一个是信号需要被采样，其次是信号被分成若干量阶。信号被采样，也就意味着我们得到的不是原先的连续的信号了，而是一个离散的一些采集的样点。那么对时域信号进行采样，必然造成频谱的周期化，如果原先频谱仅限于有限的带宽，那么周期化之后，只要周期大于原先的带宽，那么实际上没有混叠失真。而数字电路限制我们只能进行乘加等二进制域的计算，获得另一些离散的点，因此我们不得不将频谱也进行“采样”，频域的抽样导致时域上又周期化了，好在如果我们只取有限的长度，可以假定没采集的部分进行的是周期化延拓(由于平稳系统认为信号可以分解为正余弦函数的组合，而正余弦函数是可以周期延拓的，所以这个假设没有问题)，那么我们得到了时域和频域都是离散的周期延拓的点集。

既然是周期延拓的，那么延拓的部分和主值区间(靠近0的那个周期)是重复的数值，因此我们只保留主值区间的部分，这样的时域点集到频域点集的变换关系叫离散傅里叶变换(DFT)。然而它的运算过于复杂，因此库里和图基(Cooley,Tukey)两人力图化简它，找到了这个算法的一些内在运算规律，得到的运算量由原来的平方级降为NlogN级，这个算法就叫按时间抽取快速傅里叶变换，桑德和图基研究按频率抽取也可以得到类似的低复杂度算法，这类算法统称快速傅里叶变换(FFT)，FFT的计算结果和DFT是完全等价的，只是运算量降低了。又由于时频变换能量不变(Parseval定理)，所以频域的绝对数值没有意义了，只要获得相对数值即可，因此数字系统中的量化阶数以及数字系统溢出后的缩放调整对FFT的计算结果影响仅在