清华大学出版数据结构第五版的链表的使用方法_如何提升链表的性能？

链表是一种我们耳熟能详的数据结构，其重要性是不言而喻的。但是，由于链表本身的结构限制，其查找的复杂度为O(n)。而删除和插入操作，虽然，理论上是O(1)，但实际上，你必须获得其前一个结点，这导致其复杂度变成了O(n)。那么，今天，我介绍两种方法去，提升链表的性能。

1.链表的变形：跳表。

跳表是一种我们不常见的数据结构，但由于其优秀的特性，在工业中，常常被用来代替红黑树，进行查找，插入和删除。Redis的有序集合就是用跳表来实现的。

跳表本质上是采用"二分"的思路来改造链表，所以这要求链表必须是有序的。对于传统的链表，即使，其是有序的，查找起来也需要O(n)的时间复杂度。所以，我们在链表增加索引，如下图所示：

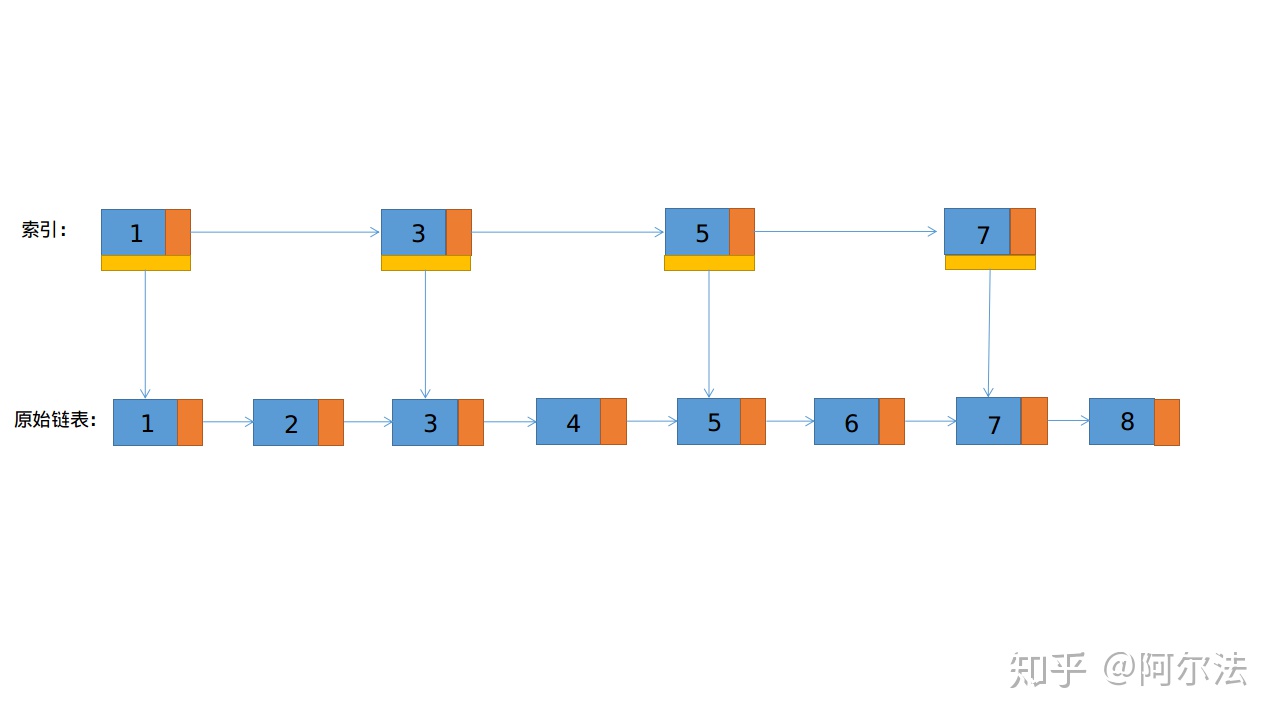
通过这种方式，当我们在查询6的时候，我们先通过索引，定位6在5之后，再通过指针，指向原始链表，得到6。通过这种方式，查找到6需要5步，原始需要6步。当然，这么看其实没有减少很多。所以我们可以继续向上加索引，如下图所示

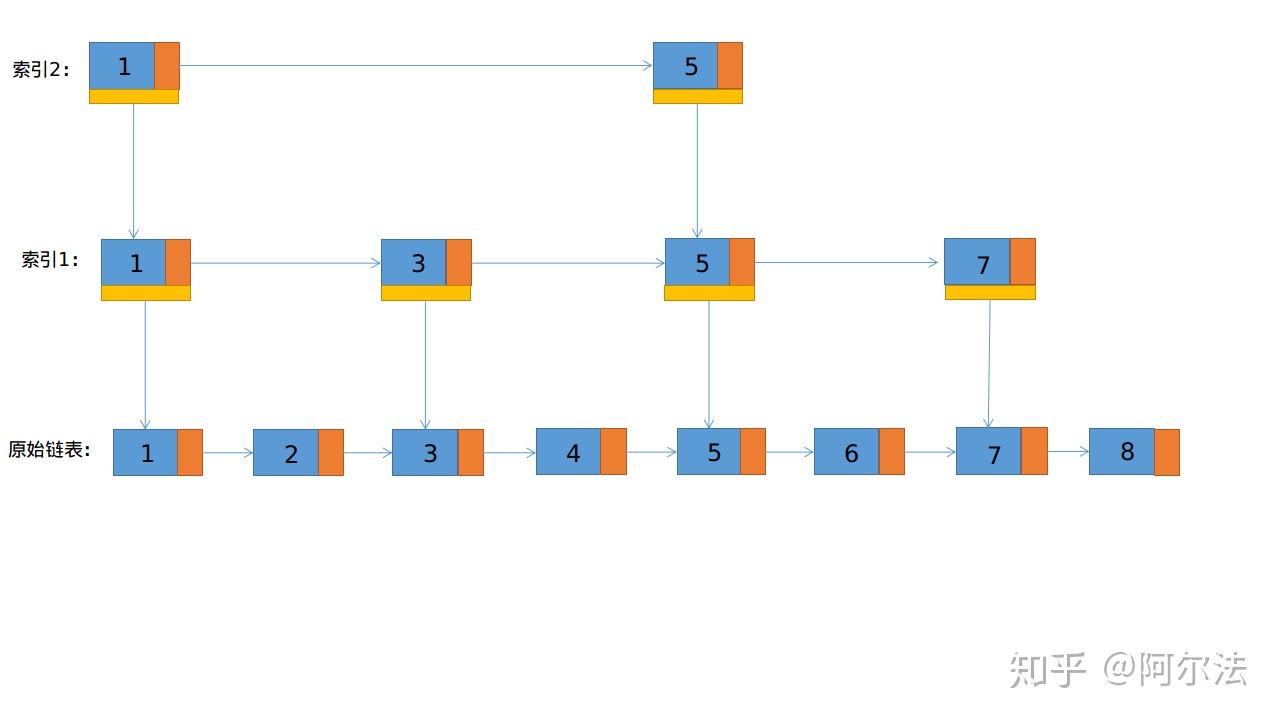
通过这种方式，在数据量很大的情况下，查找速度会有明显的的提升。不信，你可以动手画一下？

时间复杂度分析：

假设原始链表有n个结点，索引1为

，索引2为

， 以此类推，最后一层为2个结点，所以

，即索引层大概为

，每一层遍历m个结点，所以其时间复杂度为O(mlogn)。而m其实是个常数，因为从最顶层索引开始，我们可以定位查找数在两结点之间，从图中我们可以明显观察到，两结点映射到下一层，则只有3个结点。所以每层最多需要遍历3个结点。所以其时间复杂度为O(logn)。

空间复杂度：

从上可知，每层结点数为

，

，

，

，2。这是一个等比数列，通过等比数列求和公式，我们可以得到，其空间复杂度为O(n)。(天下没有免费的午餐)

这里提供一个我参考其他人的代码，给出的一个跳表的简单实现。

sccData/Data-structure-and-algorithm_self​github.com

2.散列表+链表

散列表解决散列冲突，通常有两种方法：开放地址法和链表法。所以，我们可以通过改造链表法，一方面弥补散列表无法按顺序遍历的缺点，另一方面弥补，链表无法随机访问的缺点。

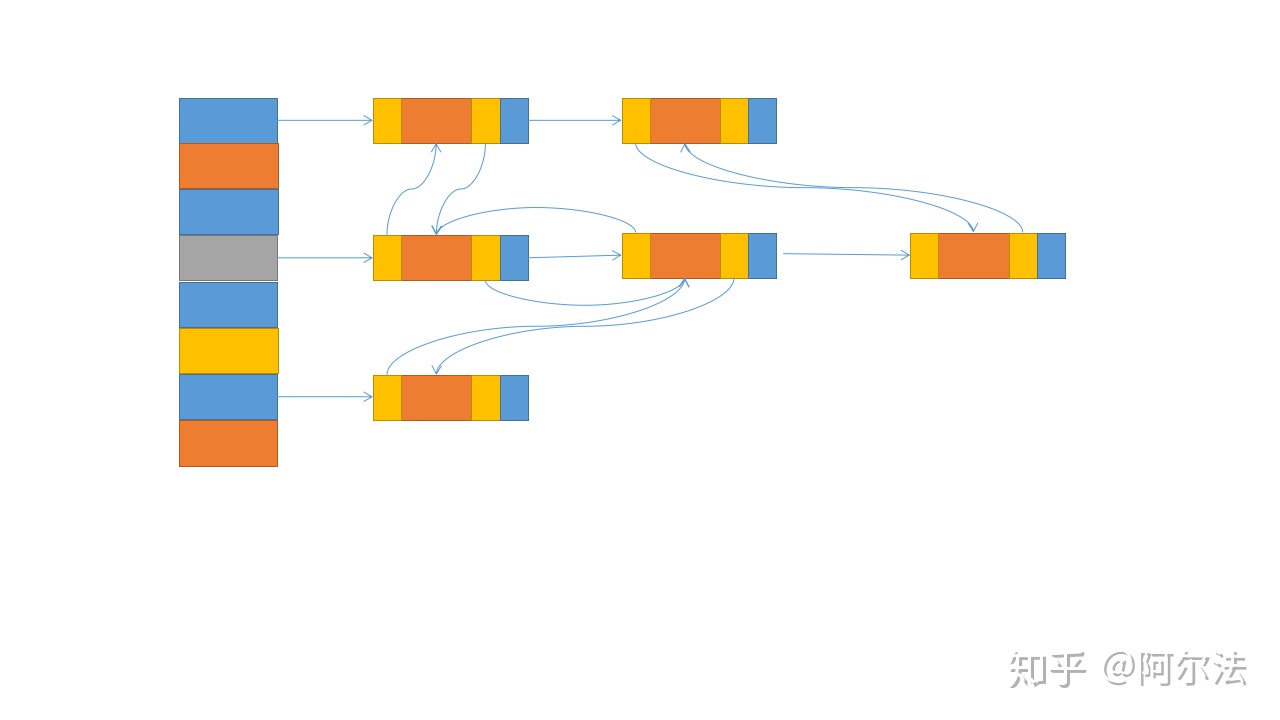
如上图所示，在链表法的基础上，使用双向链表把数据串起来，通过这种方式，我们可以把数据的查找，删除和插入的时间复杂度缩短到O(1)。另一方面，可以让散列表可以按某种顺序遍历。

下面，我们来看一个经典问题LRU淘汰缓存，在传统的单链表方式下，时间复杂度为O(n)，通过上面介绍的散列表+链表的方式，可以将时间缩短到O(1)。

下面是leetcode关于这个题目的链接，你可以试一下。

https://leetcode.com/problems/lru-cache/​leetcode.com