pcl中ransac提取直线_PCL点云曲面重建-优快云博客

本文介绍点云处理中的关键技术，包括法线估计、点云平滑、数据重采样及三角化等。通过多项式平滑实现曲面重建，并采用贪婪投影三角化算法快速构建三角网格模型。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

基于多项式平滑点云及法线估计的曲面重建
在平面模型上构造凸凹多边形
无序点云的快速三角化

基于多项式平滑点云及法线估计的曲面重建

基于移动最小二乘法（MLS）的法线估计、点云平滑和数据重采样。有时，测量较小的对象时会产生一些误差，这些误差所造成的不规则数据如果直接拿来曲面重建的话会使重建的曲面不光滑或者有漏洞。这些不规则很难用统计分析消除，所以为了建立完整的模型必须对表面进行平滑处理和漏洞修复。在不能进行额外扫描的情况下，我们可以通过对数据重采样来解决这一问题，重采样算法通过对周围数据点进行高阶多项式插值来重建表面缺少的部分。此外，由多个扫描点扫描结果配准后得到的数据直接拿来曲面重建的话会产生“双墙”等人造伪数据，即某块区域会出现重叠的两个曲面。重采样算法也可以对这个问题进行处理。

#include <pcl/point_types.h>          //PCL中所有点类型定义的头文件
#include <pcl/io/pcd_io.h>            //打开关闭pcd文件的类定义的头文件
#include <pcl/kdtree/kdtree_flann.h>  //kd-tree搜索对象的类定义的头文件
#include <pcl/surface/mls.h>          //最小二乘法平滑处理类定义头文件
int
main(int argc, char** argv)
{// 将一个适当类型的输入文件加载到对象PointCloud中
	pcl::PointCloud<pcl::PointXYZ>::Ptr cloud(new pcl::PointCloud<pcl::PointXYZ>());
	// 加载bun0.pcd文件，加载的文件在 PCL的测试数据中是存在的 
	pcl::io::loadPCDFile("rabbit.pcd", *cloud);
	// 创建一个KD树
	pcl::search::KdTree<pcl::PointXYZ>::Ptr tree(new pcl::search::KdTree<pcl::PointXYZ>);
	// 输出文件中有PointNormal类型，用来存储移动最小二乘法算出的法线
	pcl::PointCloud<pcl::PointNormal> mls_points;
	// 定义对象 (第二种定义类型是为了存储法线, 即使用不到也需要定义出来)
	pcl::MovingLeastSquares<pcl::PointXYZ, pcl::PointNormal> mls;
	mls.setComputeNormals(true);  //设置在最小二乘计算中需要进行法线估计
	//设置参数
	mls.setInputCloud(cloud);
	mls.setPolynomialFit(true);
	mls.setSearchMethod(tree);
	mls.setSearchRadius(0.03);
	// 曲面重建
	mls.process(mls_points);
	// 保存结果
	pcl::io::savePCDFile("rabbit-mls.pcd", mls_points);
}

参考1

在平面模型上构造凸凹多边形

程序说明：为平面模型的点击提取其对应的凹多边形；

1. 点云滤波；
2. 从滤波后的点云中提取平面模型；
3. 将滤波后的点云投影到平面模型中得到投影后的点云；
4. 从投影后的点云中提取凹多边形；

#include <pcl/ModelCoefficients.h>
#include <pcl/io/pcd_io.h>
#include <pcl/point_types.h>
#include <pcl/sample_consensus/method_types.h>
#include <pcl/sample_consensus/model_types.h>
#include <pcl/filters/passthrough.h>
#include <pcl/filters/project_inliers.h>
#include <pcl/segmentation/sac_segmentation.h>
#include <pcl/surface/concave_hull.h>
#include <pcl/visualization/pcl_visualizer.h>
 
int
main (int argc, char** argv)
{
  pcl::PointCloud<pcl::PointXYZ>::Ptr cloud (new pcl::PointCloud<pcl::PointXYZ>), 
                                      cloud_filtered (new pcl::PointCloud<pcl::PointXYZ>), 
                                      cloud_projected (new pcl::PointCloud<pcl::PointXYZ>);
  pcl::PCDReader reader;
 
  reader.read ("....sourcetable_scene_mug_stereo_textured.pcd", *cloud);
  
  //建立直通滤波器，消除杂散的NaN点
  pcl::PassThrough<pcl::PointXYZ> pass;
  pass.setInputCloud (cloud);   //设置输入点云
  pass.setFilterFieldName ("z");//设置分隔字段为z坐标
  pass.setFilterLimits (0, 1.1);//设置分割阈值范围，z轴上不在该范围的点过滤掉
  pass.filter (*cloud_filtered);
  std::cerr << "PointCloud after filtering has: "
            << cloud_filtered->points.size () << " data points." << std::endl;
 
  pcl::ModelCoefficients::Ptr coefficients (new pcl::ModelCoefficients);
  pcl::PointIndices::Ptr inliers (new pcl::PointIndices);//inliers指针存储点云分割后的结果
  
  // Create the segmentation object
  pcl::SACSegmentation<pcl::PointXYZ> seg;//创建分割对象
  // 可选设置
  seg.setOptimizeCoefficients (true);     //设置优化系数，该参数为可选设置
  // 必须设置
  seg.setModelType (pcl::SACMODEL_PLANE); //设置分割模型为SACMODEL_PLANE 平面模型
  seg.setMethodType (pcl::SAC_RANSAC);    //设置采样一致性估计方法模型为SAC_RANSAC
  seg.setDistanceThreshold (0.01);        //设置距离阈值为0.01， 即与估计平面模型的距离小于0.01m的点都为内点inliers
 
  seg.setInputCloud (cloud_filtered);     //设置输入点云为滤波后的点云
  seg.segment (*inliers, *coefficients);  //分割结果：平面模型
  std::cerr << "PointCloud after segmentation has: "
            << inliers->indices.size () << " inliers." << std::endl;
 
  // Project the model inliers
  pcl::ProjectInliers<pcl::PointXYZ> proj; //创建点云投影滤波对象
  proj.setModelType (pcl::SACMODEL_PLANE); //设置投影模型为SACMODEL_PLANE
  proj.setInputCloud (cloud_filtered);     //设置输入点云为滤波后的点云
  proj.setModelCoefficients (coefficients);//将估计得到的平面模型coefficients参数设置为投影平面模型系数
  proj.filter (*cloud_projected);          //将滤波后的点云投影到平面模型中得到投影后的点云cloud_projected
  std::cerr << "PointCloud after projection has: "
            << cloud_projected->points.size () << " data points." << std::endl;
 
  // Create a Concave Hull representation of the projected inliers
  pcl::PointCloud<pcl::PointXYZ>::Ptr cloud_hull (new pcl::PointCloud<pcl::PointXYZ>);
  pcl::ConcaveHull<pcl::PointXYZ> chull;//创建多边形提取对象
  chull.setInputCloud (cloud_projected);//设置输入点云为投影后的点云cloud_projected
  chull.setAlpha (0.1);                 //设置Alpha值为0.1
  chull.reconstruct (*cloud_hull);      //重建提取创建凹多边形
 
  std::cerr << "Concave hull has: " << cloud_hull->points.size ()
            << " data points." << std::endl;
 
  pcl::PCDWriter writer;
  writer.write ("table_scene_mug_stereo_textured_hull.pcd", *cloud_hull, false);
 
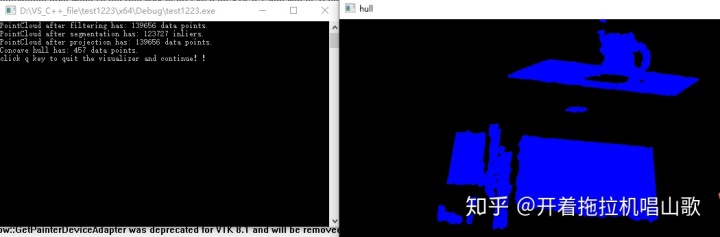
  pcl::visualization::PCLVisualizer::Ptr viewer0(new pcl::visualization::PCLVisualizer("hull"));
  viewer0->addPointCloud(cloud, pcl::visualization::PointCloudColorHandlerCustom<pcl::PointXYZ>(cloud, 0, 0, 255), "cloud");
  viewer0->setPointCloudRenderingProperties(pcl::visualization::PCL_VISUALIZER_POINT_SIZE, 4, "cloud");
  cout << "click q key to quit the visualizer and continue！！" << endl;
  viewer0->spin();
 
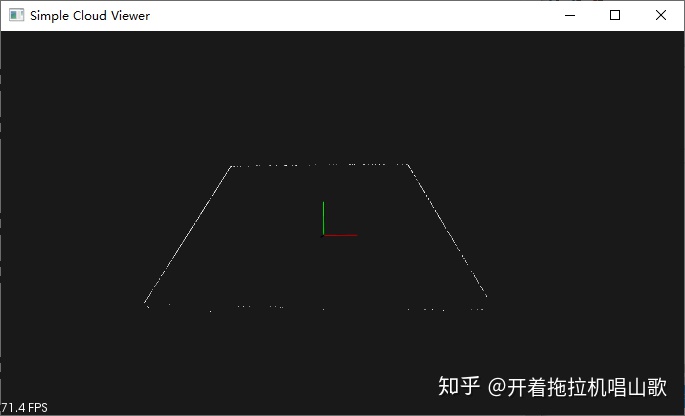
  pcl::visualization::PCLVisualizer::Ptr viewer1(new pcl::visualization::PCLVisualizer("hull"));
  viewer1->addPointCloud(cloud_hull, pcl::visualization::PointCloudColorHandlerCustom<pcl::PointXYZ>(cloud_hull, 0, 255, 0), "cloud_hull");
  viewer1->setPointCloudRenderingProperties(pcl::visualization::PCL_VISUALIZER_POINT_SIZE, 4, "cloud_hull");
  cout << "click q key to quit the visualizer and continue！！" << endl;
  viewer1->spin();
 
  return (0);
}

无序点云的快速三角化

使用贪婪投影三角化算法对有向点云进行三角化，

具体方法是：

（1）先将有向点云投影到某一局部二维坐标平面内

（2）在坐标平面内进行平面内的三角化

（3）根据平面内三位点的拓扑连接关系获得一个三角网格曲面模型.

将三维点通过法线投影到某一平面，然后对投影得到的点云作平面内的三角化，从而得到各点的连接关系。在平面区域三角化的过程中用到了基于 Delaunay 的空间区域增长算法，该方法通过选取一个样本三角片作为初始曲面，不断扩张曲面边界，最后形成一张完整的三角网格曲面。最后根据投影点云的连接关系确定各原始三维点间的拓扑连接，所得三角格网即为重建得到的曲面模型。

贪婪投影三角化算法是一种对原始点云进行快速三角化的算法。该算法假设曲面光滑，点云密度变化均匀，不能在三角化的同时对曲面进行平滑和孔洞修复。

使用贪婪投影三角化算法对有向点云进行三角化，具体方法是先将有向点云投影到某一局部二维坐标平面内，再在坐标平面内进行平面内的三角化，再根据平面内三位点的拓扑连接关系获得一个三角网格曲面模型。贪婪投影三角化算法原理是处理一系列可以使网格“生长扩大”的点（边缘点），延伸这些点直到所有符合几何正确性和拓扑正确性的点都被连上。该算法的优点是可以处理来自一个或者多个扫描仪扫描得到并且有多个连接处的散乱点云。但该算法也有一定的局限性，它更适用于采样点云来自于表面连续光滑的曲面并且点云密度变化比较均匀的情况。

该算法中的三角化过程是局部进行的，首先沿着一点的法线将该点投影到局部二维坐标平面内并连接其他悬空点，然后在进行下一点。

参考1

#include <pcl/point_types.h>
#include <pcl/io/pcd_io.h>
#include <pcl/kdtree/kdtree_flann.h>
#include <pcl/features/normal_3d.h>
#include <pcl/surface/gp3.h>
#include <pcl/visualization/pcl_visualizer.h>
#include <boost/thread/thread.hpp>
 
int
main (int argc, char** argv)
{
  // Load input file into a PointCloud<T> with an appropriate type
  pcl::PointCloud<pcl::PointXYZ>::Ptr cloud (new pcl::PointCloud<pcl::PointXYZ>);
  pcl::PCLPointCloud2 cloud_blob;
  pcl::io::loadPCDFile ("....sourcetable_scene_lms400_downsampled.pcd", cloud_blob);
  pcl::fromPCLPointCloud2(cloud_blob, *cloud);
  //* the data should be available in cloud
 
  // Normal estimation*
  pcl::NormalEstimation<pcl::PointXYZ, pcl::Normal> n;//设置法线估计对象
  pcl::PointCloud<pcl::Normal>::Ptr normals (new pcl::PointCloud<pcl::Normal>);//存储估计的法线
  pcl::search::KdTree<pcl::PointXYZ>::Ptr tree (new pcl::search::KdTree<pcl::PointXYZ>);//定义kd树指针
  tree->setInputCloud (cloud);//用cloud构造tree对象
  n.setInputCloud (cloud);//为法线估计对象设置输入点云
  n.setSearchMethod (tree);//设置搜索方法
  n.setKSearch (20);//设置k邻域搜素的搜索范围
  n.compute (*normals);//估计法线
  //* normals should not contain the point normals + surface curvatures
 
  // Concatenate the XYZ and normal fields*
  pcl::PointCloud<pcl::PointNormal>::Ptr cloud_with_normals (new pcl::PointCloud<pcl::PointNormal>);//
  pcl::concatenateFields (*cloud, *normals, *cloud_with_normals);//连接字段，cloud_with_normals存储有向点云
  //* cloud_with_normals = cloud + normals
 
  // Create search tree*
  pcl::search::KdTree<pcl::PointNormal>::Ptr tree2 (new pcl::search::KdTree<pcl::PointNormal>);//定义搜索树对象
  tree2->setInputCloud (cloud_with_normals);//利用有向点云构造tree
 
  // Initialize objects
  pcl::GreedyProjectionTriangulation<pcl::PointNormal> gp3;//定义三角化对象
  pcl::PolygonMesh triangles;//存储最终三角化的网络模型
 
  // Set the maximum distance between connected points (maximum edge length)
  gp3.setSearchRadius (0.025);         //设置搜索半径radius，来确定三角化时k一邻近的球半径。
 
  // Set typical values for the parameters
  gp3.setMu (2.5);                     //设置样本点到最近邻域距离的乘积系数 mu 来获得每个样本点的最大搜索距离，这样使得算法自适应点云密度的变化
  gp3.setMaximumNearestNeighbors (100);//设置样本点最多可以搜索的邻域数目100 。
  gp3.setMaximumSurfaceAngle(M_PI/4);  //45 degrees，设置连接时的最大角度 eps_angle ，当某点法线相对于采样点的法线偏离角度超过该最大角度时，连接时就不考虑该点。
  gp3.setMinimumAngle(M_PI/18);        //10 degrees，设置三角化后三角形的最小角，参数 minimum_angle 为最小角的值。
  gp3.setMaximumAngle(2*M_PI/3);       //120 degrees，设置三角化后三角形的最大角，参数 maximum_angle 为最大角的值。
  gp3.setNormalConsistency(false);     //设置一个标志 consistent ，来保证法线朝向一致，如果设置为 true 则会使得算法保持法线方向一致，如果为 false 算法则不会进行法线一致性检查。
 
  // Get result
  gp3.setInputCloud (cloud_with_normals);//设置输入点云为有向点云
  gp3.setSearchMethod (tree2);           //设置搜索方式tree2
  gp3.reconstruct (triangles);           //重建提取三角化
 // std::cout << triangles;
  // Additional vertex information
  std::vector<int> parts = gp3.getPartIDs();//获得重建后每点的 ID, Parts 从 0 开始编号， a-1 表示未连接的点。
  /*
  获得重建后每点的状态，取值为 FREE 、 FRINGE 、 BOUNDARY 、 COMPLETED 、 NONE 常量，
  其中 NONE 表示未定义， 
  FREE 表示该点没有在 三 角化后的拓扑内，为自由点， 
  COMPLETED 表示该点在三角化后的拓扑内，并且邻域都有拓扑点，
  BOUNDARY 表示该点在三角化后的拓扑边缘， 
  FRINGE 表示该点在 三 角化后的拓扑内，其连接会产生重叠边。
  */
  std::vector<int> states = gp3.getPointStates();
 
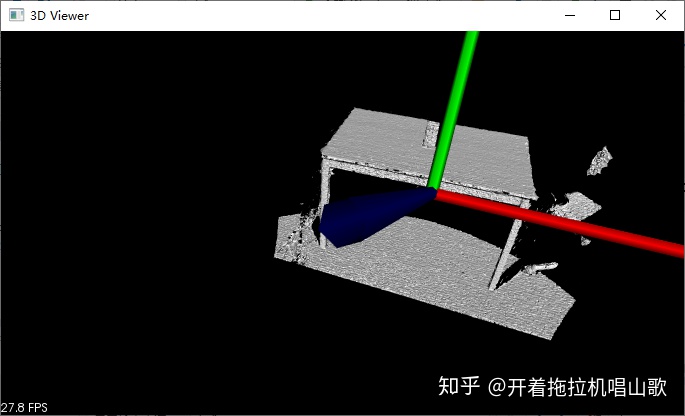
  boost::shared_ptr<pcl::visualization::PCLVisualizer> viewer (new pcl::visualization::PCLVisualizer ("3D Viewer"));
  viewer->setBackgroundColor (0, 0, 0);
  viewer->addPolygonMesh(triangles,"my");
 
  viewer->addCoordinateSystem (1.0);
  viewer->initCameraParameters ();
   // 主循环
  while (!viewer->wasStopped ())
  {
    viewer->spinOnce (100);
    boost::this_thread::sleep (boost::posix_time::microseconds (100000));
  }
  // Finish
  return (0);
}