高斯消元法线性方程组python_高斯消元法解线性方程组mpi并行

最新推荐文章于 2023-05-03 17:30:13 发布

原创

最新推荐文章于 2023-05-03 17:30:13 发布

· 650 阅读

3 ·

版权

文章标签：

#高斯消元法线性方程组python

本文介绍了高斯消元法解决线性方程组的基本思想，以及如何利用MPI进行并行计算优化。通过正向迭代构建上三角阵，然后在有唯一解的情况下反向迭代得到解。文章还讨论了并行计算中可并行的部分，并提供了Python的MPI并行代码示例。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

一，高斯消元法简介

将线性方程组写成矩阵的形式，通过两行交换或者某一行加另一行的k倍，构造上三角阵，跟据扩展矩阵秩的关系判断解的个数。

二，hpl标准（一个高性能计算的评测标准，可跳过）

HPL是针对现代并行计算机提出的测试方式，Linpack是国际上最流行的用于测试高性能计算机系统浮点性能的benchmark。HPL采用高斯消元法求解线性方程组。求解问题规模为N时，浮点运算次数为(2/3 * N^3－2*N^2)。因此，只要给出问题规模N，测得系统计算时间T，峰值=计算量(2/3 * N^3－2*N^2)/计算时间T，测试结果以浮点运算每秒(Flops)给出，衡量计算机性能的一个重要指标就是计算峰值或者浮点计算峰值。HPL测试结果是TOP500排名的重要依据。

三、秩与解的关系

equation?tex=R%28a%29%3CR%28ab%29%E6%97%A0%E8%A7%A3%EF%BC%8C+R%28a%29%3DR%28ab%29%3Cn%E6%9C%89%E6%97%A0%E7%A9%B7%E8%A7%A3%EF%BC%8C+R%28a%29%3DR%28ab%29%3Dn%E6%9C%89%E5%94%AF%E4%B8%80%E8%A7%A3

四、高斯消元法思路

1，正向迭代，构造上三角阵，每次消除一列，如下

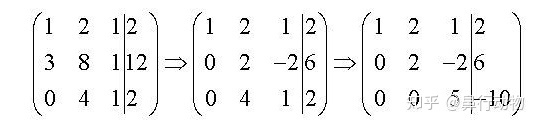
def gauss(matrix_a,matrix_b):
    if not np.all(matrix_b==0):
        augmented=np.concatenate([matrix_a,matrix_b],1)  # 拼接增广矩阵
    else:
        augmented=matrix_a

    row=augmented.shape[0]  # 行数
    col=augmented.shape[1]  # 列数
    for j in range(col):
        if j>=r

最低0.47元/天解锁文章