传统的线性降维方法效果不佳。_PCA（主程序分析）降维原理小结与实例

1.主成分分析（Principal components analysis，以下简称PCA）是最重要的降维方法之一。在数据压缩消除冗余和数据噪音消除等领域都有广泛的应用。一般我们提到降维最容易想到的算法就是PCA，目标是基于方差提取最有价值的信息，属于无监督问题。但是降维后的数据因为经过多次矩阵的变化我们不知道降维后的数据意义，但是更加注重降维后的数据结果。

2.向量的表示及基的变换（基：数据的衡量标准，之所以有坐标点（3，2）是因为有x、y轴）：

基变换：基是正交的（即内积为0或者说相互垂直）

要求：线性无关（x轴和y轴的数据互补影响）

变换：数据与一个基做内积运算，结果作为第一个新的坐标分量，然后与第二个基做内积运算，结果作为第二个新坐标的分量。

3.现在已经知道基变换的原理，那么现在问题又落在如何找到一组合适的基呢？

（1）目标：寻找一个一维基，使得变换为这个基上的坐标表示后，方差最大，也寄投影后的投影值尽可能分散。

（2）方差：描述的是样本集合的各个样本点到均值的距离之平均，一般用来描述一维数据的

在概率论和统计方差用来度量随机变量和数据期望之间的偏离程度。

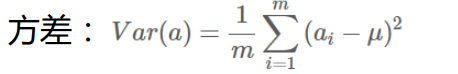
协方差：是一种用来度量两个随机变量关系的统计量，只能处理二维问题。

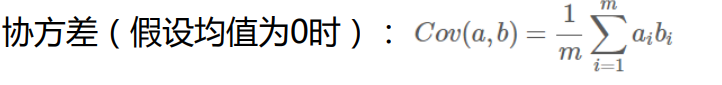
方差和协方差的关系：方差是用来度量单个变量的“自身变异大小”的总体参数，方差越大表面该变量变异越大。协方差是两个变量相互影响大小的参数，协方差的参数越大，则两个变量相互影响越大。

（3）如果单纯的选择方差最大的方向，后续方向应该个方差最大的方向接近重合，如果接近重合，那么特征之间几乎都是线性相关的，这显然不是我们想要的。

这时引入协方差。如果协方差为0，表示两个特征是线性无关的，所以为了尽可能的展示数据更多的原始信息，我们需要特征之间是线性无关的，也即协方差为0.第一个坐标轴选择方差最大的，为了是的协方差为0，选择第二个基时只能在第一个基正交的平面上选择。

4.优化目标：将一组N维向量降为K（0<k<n）维，目标选择K个单位正交基，使得原始数据变换到这组基上后，各字段两两间协方差为0，字段的方差尽可能最大。

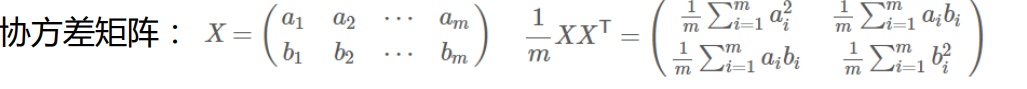
协方差矩阵对角线上的元素分别是字段的方差，而其他元素是a和b的协方差。并且是实对称矩阵。

到此求出特征值和特征向量，并由此求出最后的解。

5.PCA实例：

6. PCA算法总结

　　　　这里对PCA算法做一个总结。作为一个非监督学习的降维方法，它只需要特征值分解，就可以对数据进行压缩，去噪。因此在实际场景应用很广泛。为了克服PCA的一些缺点，出现了很多PCA的变种，比如第六节的为解决非线性降维的KPCA，还有解决内存限制的增量PCA方法Incremental PCA，以及解决稀疏数据降维的PCA方法Sparse PCA等。

　　　　PCA算法的主要优点有：

　　　　1）仅仅需要以方差衡量信息量，不受数据集以外的因素影响。　

　　　　2）各主成分之间正交，可消除原始数据成分间的相互影响的因素。

　　　　3）计算方法简单，主要运算是特征值分解，易于实现。

　　　　PCA算法的主要缺点有：

　　　　1）主成分各个特征维度的含义具有一定的模糊性，不如原始样本特征的解释性强。

　　　　2）方差小的非主成分也可能含有对样本差异的重要信息，因降维丢弃可能对后续数据处理有影响。

二、基于sklearn实现PCA降维

1. sklearn.decomposition.PCA参数介绍

　　　　下面我们主要基于sklearn.decomposition.PCA来讲解如何使用scikit-learn进行PCA降维。PCA类基本不需要调参，一般来说，我们只需要指定我们需要降维到的维度，或者我们希望降维后的主成分的方差和占原始维度所有特征方差和的比例阈值就可以了。

　　　　现在我们对sklearn.decomposition.PCA的主要参数做一个介绍：

　　　　1）n_components：这个参数可以帮我们指定希望PCA降维后的特征维度数目。最常用的做法是直接指定降维到的维度数目，此时n_components是一个大于等于1的整数。当然，我们也可以指定主成分的方差和所占的最小比例阈值，让PCA类自己去根据样本特征方差来决定降维到的维度数，此时n_components是一个（0，1]之间的数。当然，我们还可以将参数设置为"mle", 此时PCA类会用MLE算法根据特征的方差分布情况自己去选择一定数量的主成分特征来降维。我们也可以用默认值，即不输入n_components，此时n_components=min(样本数，特征数)。

　　　　2）whiten ：判断是否进行白化。所谓白化，就是对降维后的数据的每个特征进行归一化，让方差都为1.对于PCA降维本身来说，一般不需要白化。如果你PCA降维后有后续的数据处理动作，可以考虑白化。默认值是False，即不进行白化。

　　　　3）svd_solver：即指定奇异值分解SVD的方法，由于特征分解是奇异值分解SVD的一个特例，一般的PCA库都是基于SVD实现的。有4个可以选择的值：{‘auto’, ‘full’, ‘arpack’, ‘randomized’}。randomized一般适用于数据量大，数据维度多同时主成分数目比例又较低的PCA降维，它使用了一些加快SVD的随机算法。 full则是传统意义上的SVD，使用了scipy库对应的实现。arpack和randomized的适用场景类似，区别是randomized使用的是scikit-learn自己的SVD实现，而arpack直接使用了scipy库的sparse SVD实现。默认是auto，即PCA类会自己去在前面讲到的三种算法里面去权衡，选择一个合适的SVD算法来降维。一般来说，使用默认值就够了。

　　　　除了这些输入参数外，有两个PCA类的成员值得关注。第一个是explained_variance_，它代表降维后的各主成分的方差值。方差值越大，则说明越是重要的主成分。第二个是explained_variance_ratio_，它代表降维后的各主成分的方差值占总方差值的比例，这个比例越大，则越是重要的主成分。

1.首先生成随机数据并可视化

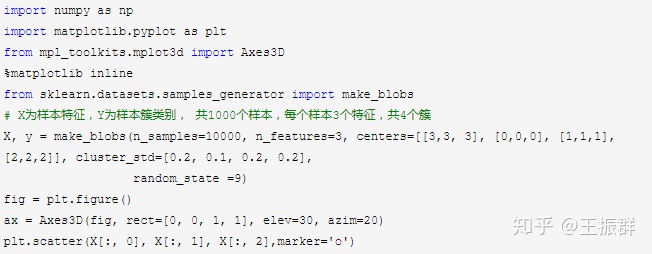
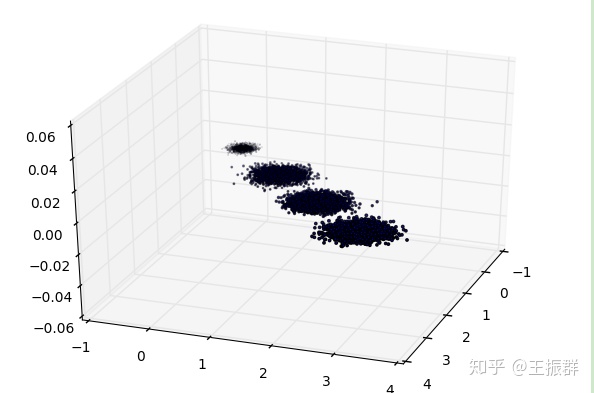
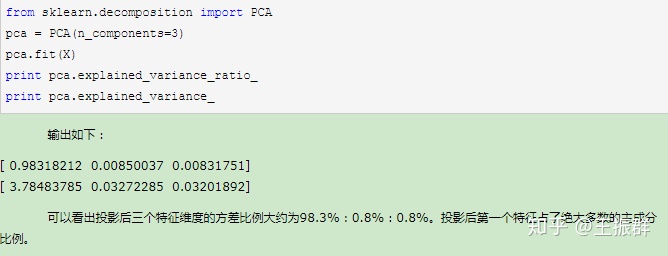
2.我们先不降维，只对数据进行投影，看看投影后的三个维度的方差分布，代码如下：

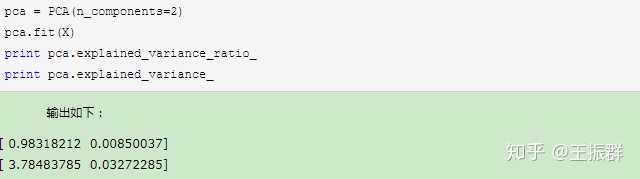
3.我们将数据从三维降到二维

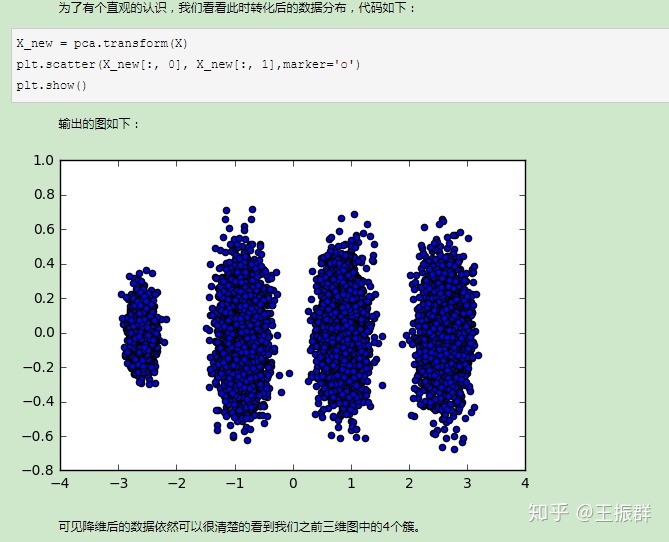
这个结果其实可以预料，因为上面三个投影后的特征维度的方差分别为：[ 3.78483785 0.03272285 0.03201892]，投影到二维后选择的肯定是前两个特征，而抛弃第三个特征

3.现在我们看看不直接指定降维的维度，而指定降维后的主成分方差和比例

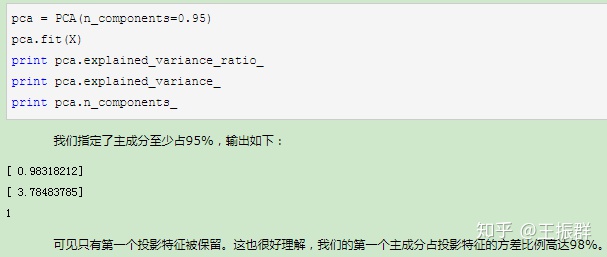
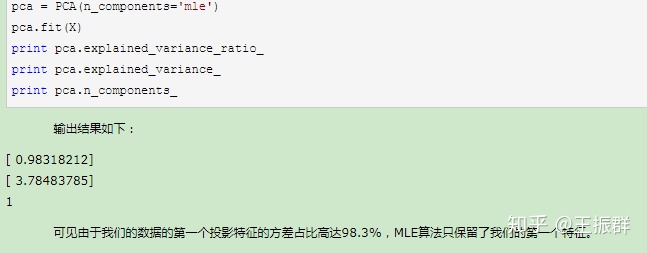
4、最后我们看看让MLE算法自己选择降维维度的效果

参考：刘建平博客园