希尔排序时间复杂度_堆排序时间复杂度分析

堆排序的实现

首先我们看一下堆排序的实现代码

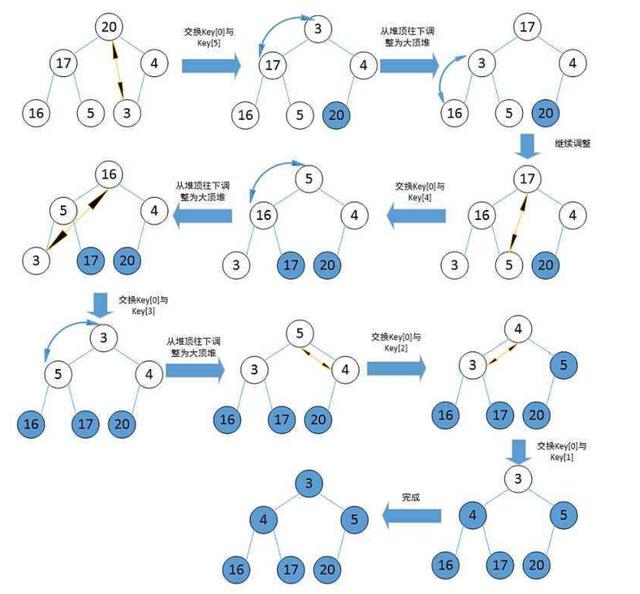
堆排序

堆排序主要由两部分组成堆初始化和重建堆

堆初始化和堆重建的核心都是堆调整，即递归的将大根置于堆顶(大顶堆)或者小根置堆顶(小顶堆)

堆初始化算法复杂度

堆初始化即从最底层的一个父结点(即倒数第二层)开始调整排序。我们可以这样分析，对于一个深度为h的堆而言。第一层共有一个结点，最多可能调整h-1次。对于倒数第二层共有2^(h-2)个结点，最多只要比较调整一次。分析可得，对于第n层而言，共需调整2^(n-1)(h-n)。

因此我们可以得出初始堆的算法复杂度为

O(n)=2^0(h-1)+2^1(h-2)+......+2^(h-2)1+2^(h-1)0

2O(n)=2^1(h-1)+2^2(h-2)+....+2^(h-1)1+2^(h)0

所以O(n)=2^1+2^2+.....2^(h-1)-h+1=2^h-h-1=n-log(n)-1。

因此堆初始化的时间复杂度是O(n)

重建堆的算法时间复杂度

重建堆的步骤为将堆顶放置于堆尾，然后排出堆尾后重新建立堆，每次调整的算法时间复杂度是log(n)

我们分析一下其时间负责度为

O(n)=log(1)+log(2)+.....+log(n)=log(n!)

log(n!)与nlog(n)是同阶层

堆排序的时间复杂度

因此整个的堆排序时间复杂度是

O(n+nlogn)=O(nlog)