python f检验 模型拟合度_多元线性回归模型检验和预测

一、概述

（F检验）显著性检验：检测自变量是否真正影响到因变量的波动。

（t检验）回归系数检验：单个自变量在模型中是否有效。

二、回归模型检验

检验回归模型的好坏常用的是F检验和t检验。F检验验证的是偏回归系数是否不全为0（或全为0），t检验验证的是单个自变量是否对因变量的影响是显著的（或不显著）。

F检验和t检验步骤：

提出问题的原假设和备择假设

在原假设的条件下，构造统计量

根据样本信息，计算统计量的值

对比统计量的值和理论F分布的值，计算统计量的值超过理论值，则拒绝原假设，否则接受原假设

待检验数据集先构造成向量的模式：

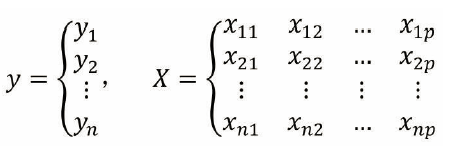
可表示成如下形式：

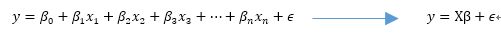
其中β 为n×1的一维向量。

1) 假设

F检验假设：

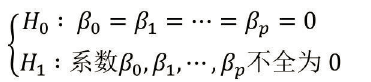
t检验假设：

H0为原假设，H1为备择假设。F检验拒绝原假设的条件为计算的F检验的值大于查到的理论F值。t检验可以通过P值和拟合优度判断变量的显著性及模型组合的优劣。

2）计算过程

F检验计算过程：

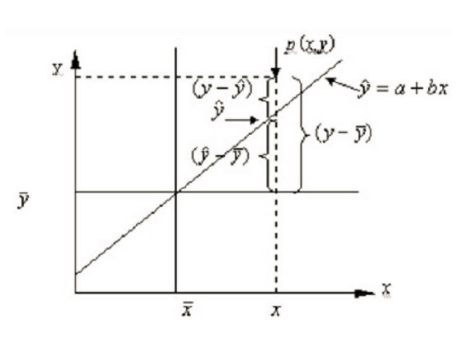
上图为假设其中一个点所在的平面，由以上点计算出ESS(误差平方和)，RSS（回归离差平方和）,TSS（总的离差平方和）。

计算公式为：

其中ESS和RSS都会随着模型的变化而发生变化（估计值变动）。而TSS衡量的是因变量和均值之间的离差平方和，不会随着模型的变化而变化。

由以上公式构造F统计量：

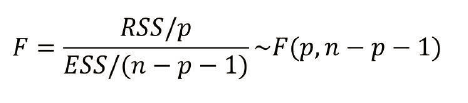
（n为数据集向量的行数，p为列数（自变量的个数），n为离差平方和RSS的自由度，n-p-1为误差平方和ESS的自由度），模型拟合越好，ESS越小，RSS越大，F值越大。

3）python中计算F值得方法：可以直接通过model.fvalue得到f值或者通过计算得到。

from sklearn import model_selection

import statsmodels.api as sm

import pandas as pd

import numpy as np

import matplotlib.pyplot as plt

from sklearn import preprocessing

Profit = pd.read_excel(r'Predict to Profit.xlsx')

Profit.head()

dummies = pd.get_dummies(Profit.State,prefix = 'State')

Profit_New = pd.concat([Profit,dummies],axis=1)

Profit_New.drop(labels = ['State','State_New York'],axis =1,inplace = True)

train , test = model_selection.train_test_split(Profit_New,test_size = 0.2,random_state=1234)

model = sm.formula.ols('Profit~RD_Spend+Administration+Marketing_Spend+State_California+State_Florida',data = train).fit()

ybar = train.Profit.mean()

p = model.df_model #自变量个数

n= train.shape[0] #行数，观测个数

RSS = np.sum((model.fittedvalues - ybar)**2) #计算离差平方和 估计值model.fittedvalues

ESS = np.sum(model.resid**2) #计算误差平方和，误差表示model.resid

F = RSS/p/(ESS/(n-p-1))

print( F, model.fvalue)

结果如下：

求理论F值，使用Scipy库子模块stats中f.ppf

from scipy.stats import f

F_Theroy = f.ppf(q=0.95,dfn = p,dfd = n-p-1)

F_Theroy