r语言 数列前m项求和_数列专题4-求和最值问题

​某些等差数列求和，会产生最大值或最小值，在n等于多少时取得最值，最值是多少，这是一个难点，在这里我们介绍两种方法。

这是倒数第2个选择题，我们一起来看：

解：设正项等比数列{an}的公比为q(q>0),因为a3=8,a4+a5=6,

到达这里时很多同学还没有问题，依据等比数列性质，解对数，等差数列求和求得。此时需要观察左边是Tn/n数列的前n项和，并且是它的最大值都应小于t。

第一种通过求和表出最大值：Tn/n我们以求得，是等差数列，我们用求和公式求出它的和。

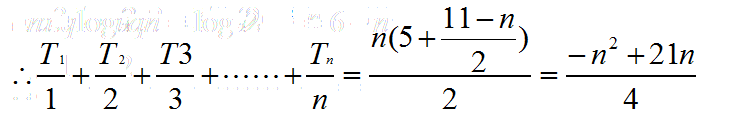
此时发现求和所得为为二次函数（关于n的二次函数），此时开口向下，即在对称轴处取得最大值。

n=-b/2a=10.5,但n要为正正整数，所以n=10或11,此时最大值为55/2，此时满足条件的最小正整数t为28。

第二种从通项观察理解：此时通项Tn/n=(11-n)/2,发现它为等差数列，并且首项为5，公差小于0，逐渐递减，要想他的和最大，只要保证他的每一项都大于等于0，下一项就小于0，此时的前n项和最大。

Tn/n=(11-n)/2大于等于0，即求得n小于等于11,即n=10或11时，此时最大值为55/2，此时满足条件的最小正整数t为28。

等差数列的求和最大最小问题，均可以通过这两种方法解决：一是求和得到二次函数，在对称轴（或离对称轴最近的正整数）取得；二是通项公式大于或小于等于0时解出的n处取得。

视频讲解

知乎视频​www.zhihu.com

有什么需要帮助的，关注我的公粽号“高中数学谭老师”，或者私信问我，帮你解答。