计算机中堆栈的应用举例,链表与栈的典型应用——简单计算机的实现

先来看一个粗糙的简单计算器的实现。他只支持加减乘除，并且一次只能对两个小于10的正整数做一次运算

点击(此处)折叠或打开

#include

int char2number(char c){

switch(c){

case '0':return 0;

case '1':return 1;

case '2':return 2;

case '3':return 3;

case '4':return 4;

case '5':return 5;

case '6':return 6;

case '7':return 7;

case '8':return 8;

case '9':return 9;

}

}

int is_operator(char c){

return (c=='*' || c=='+' || c=='-' ||c=='/');

}

int count(int a,int b,char opt){

switch(opt){

case '*':return a*b;

case '+':return a+b;

case '-':return a-b;

case '/':return a/b;

}

}

int main(void){

int number[2]; //存放运算数

char str[10]; ///表达式

char opt; //操作符

while(1){

fgets(str,10,stdin);

int i=0;

int j=0;

int res;

//相当于一个简单的字符串分析，从中提取出数字和运算符

while(str[i] && str[i]!='\n'){

if(!is_operator(str[i])){

number[i-j] =char2number(str[i]);

}else{

opt =str[i];

j++; //碰到运算符，需要记录。因为运算符并不存储在number数组中，

//比如 3*5 分析到字符5时，i为2但是number数组中只记录了3即number[0]所以5应该在number[1]，

//所以上面使用number[i-j]来记录数字

}

i++;

}

res=count(number[0],number[1],opt);

printf("=%d\n",res);

}

return 0;

}

这是一个粗糙的实现，但是但是仍旧有一些要点体现在上面，比如对 表达式的分析中使用了while(str[i] && str[i]!='\n')

我们首先要判断是不是到表达式字符串 的结尾了，如果不是还要判断是不是'\n'字符。因为调用fgets输入表达式时回车键也被存储了。

上面的程序只能进行一次 两个小于十的正整数 的加减乘除运算。如下

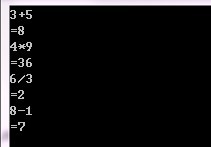
当然，这连个简单的计算器都算不上。

1： 如果我要计算 2+3+4怎么办。也就是说上面的不支持大于两个操作数的运算

2 ：如果我要 计算2的立方怎么办 。也就是说上面支持的运算太少了，这个其实问题不大。因为我们通过加单的添加就可以了。所以后面的正真实现中我们还是只实现了加减乘除四个典型运算以及带括号的运算

3 ：如果我要计算 2+3*4怎么办？有的人可能会问，这有什么怎么办了。计算就好了。但是我们知道应该先算 3*4 然后再 +2

但是计算器不知道啊。也就是说上面的并未支持优先级。这在windows自带的计算机上有体现

在查看里面将计算器切换到标准型

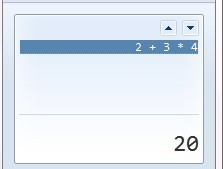
再切换到科学型。

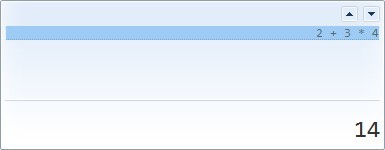
很显然，标准型并未支持优先级运算，他只是简单的从左往右运算

4 ：如果我要计算 20+10怎么办，也就是说运算数可以是任意的并不固定为小于十的正整数，因为我们输入的一个连续的 表达式字符串。

那么就需要更复杂一点的语句分析才能提取出正真的数字。当然后面的正真实现中，也只是实现了 整形所能表示的正整数的相加，并未实现小数，负数之类。当然他们原理都是相同的，只是在表达式的分析上复杂一些而已。

所以，即使是一个简单的计算器，也应该上面的四个要求。

1,2, 4，的要求主要在表达式字符串的分析上，也就是从里面分析出 字符 和数字。无非是语法分析变复杂一点。

问题核心是在 如何运算符的优先级上。

这就需要了解 后缀(逆波兰)表达式。

定义：不包含括号，运算符放在两个运算对象的后面，所有的计算按运算符出现的顺序，

严格从左向右进行(不再考虑运算符的优先规则，如：(2 + 1) * 3 ， 即2 1 + 3 *

我们知道计算机并不知道什么优先级。最简单的它只会从左到有读取然后运算。

那么根据上面 后缀表达式的定义。如果能将表达是转换成后缀表达式，那么运算就简单了。可以使用一个栈来实现。

比如：3+12*2-(6+1)*2；

转换成后缀表达式 3 12 2 * + 6 1 + 2 * -

使用一个栈，然后从左到右遍历，遇到数字我们就其入栈，遇到运算符，就出栈两个数字然后做运算，并将运算结构入栈。这样一直下去到最后。栈中存放的就为最终的结果

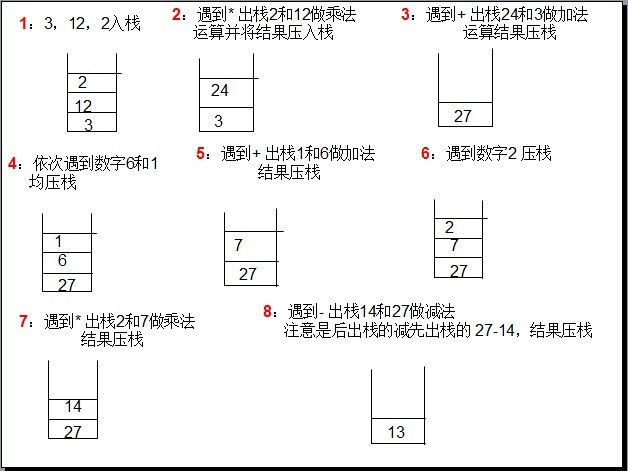
也就是说如果得到了后缀表达式那么就可以用上面的方法来从左到右计算了。而不存在优先级的问题了

那么，现在问题就变成了怎么将表达式变成计算机易于计算的后缀表达式，这里同样是用到栈来实现的。

下面我们通过对 + *以及( )这几个典型的运算符的处理 来阐述转换成后缀表达式的一般原理。

我们假设表达式是合法的。当读到一个操作数的时候，立即把他放到输出中。

遇到其他运算符时"+" ,"*" ， "("  那么久从栈中弹出元素直到当前栈顶元素的优先级比当前遇到的运算符低，然后再将该运算符入栈需要注意

的一点是 除非是在处理一个右括号')'否则绝不从栈中移走左括号'('。

如果遇到右括号')'，那么就将栈元素弹出并写到输出，直到遇到一个对应的左括号。注意：这时候右括号不入栈，弹出的左括号也不输出。而是仅仅丢弃他们

最后当我们读到表达式的结尾时，再将栈中的元素依次弹出写到输出中直到栈空变得到了后缀表达式

比如  a+b*c+(d*e+f)*g

后缀表达式为： a b c  *  +  d  e  * f  + g  * +

转换过程如下

得到后缀表达式后一切就简单了，计算机只需想上面说的那样从左到右简单计算就行了。

下面我们对 计算器编写过程中的几个核心部分的代码详细说明

整体思路是 从键盘得到一个字符串形式的表达式，然后从左到右对其进行分析，依次分离出数字和运算符然并创建对应节点，

然后像上面介绍的放法一样，如果是数字就 插入到一个链表中(这里并不输出而是放到链表中供后续使用)，如果是运算符，就放入栈中。

最终当分析表达式结尾时，弹出栈中所有元素并依此插入链表中，最终链表就是我们需要的后缀表达式。

然后对链表从左到右遍历并使用之前所说的对后缀表达式的计算方法。计算出最终结果

需要注意的是，我们没有做错误检查，所以输入的表达式必须是合法的

点击(此处)折叠或打开

enum PRIORITY{level1,level2,level3,level4};

struct node{

long        key;            //运算符或数字

PRIORITY    priority;        //优先级 数字默认设置为1 加减为2 乘除为3 括号为4

TYPE        type;            //区分当前节点中的值是 数字还是 运算符

NODE        next;

};

struct expression{

NODE exp;

NODE last_node;            //因为使用链表作为后缀表达式的存放，每次插入元素都是从尾部插入，为避免每次都要从头遍历到尾部，

//我们设置一个尾部指针,从而使插入操作能立刻完成

};

求后缀表达式的代码注释

点击(此处)折叠或打开

EXP to_postfix(char    *exp){    //求后缀表达式

EXP list;

EXP stack;

init_expression(&list); //初始化用来存放后缀表达式的链表

init_expression(&stack);    //初始化用来得到后缀表达式而是用的栈

NODE temp;

NODE new_node;

NODE top_node;

long key=0;

while(*exp && (*exp)!='\n'){ //开始遍历表达式

if('0' <=*exp && *exp<='9'){                    //这段代码用来提取出像 200 这样不是以为字符表示的数字

while('0' <=*(exp+1) && *(exp+1)<='9'){        //

key =key*10+tonumber(*exp);                //

exp++;                                    //

}                                            //

key =key*10+tonumber(*exp);                    //

new_node=create_node(key,IS_NUMBER);        //创建一个 数字类型的节点 插入链表

insert_key(list,new_node);

key=0;        //重新置0,记录后面的数字

}

else{            //不是数字则是运算符

if(*exp == ')'){                                    //如果碰到的是右括号

NODE local;                                        //则弹出栈元素 直到遇到左括号

while((char)(local=pop(stack))->key !='(' )        // 左右括号丢弃，其他运算符插入链表中(后缀表达式中)

insert_key(list,local);                        //

}else{

new_node=create_node(*exp,IS_OPERATOR);                            //不是右括号，则为一般的运算符

top_node=get_top(stack);                                         //我们尝试或得栈顶元素(不出栈)看优先级是不是小于当前遇到的

if((!top_node) || (top_node->priority < new_node->priority)){    //如果栈空，或者栈顶运算符优先级小于当前运算符

push(stack,new_node);                                        //则当前运算符直接入栈

}else{                                                                //

while(get_top(stack) && get_top(stack)->priority != level4        //

&& (get_top(stack))->priority >= new_node->priority){    //

temp=pop(stack);                                            //否则弹出栈顶元素，并插入链表中(后缀表达式存放的地方)

insert_key(list,temp);                                        //直到栈顶元素优先级小于当前遇到的运算符优先级

}                                                                //注意，除非遇到右括号，否则不能弹出左括号

push(stack,new_node);                                    //最后入栈当前遇到的运算符

}

}

}

exp++;

}

while(get_top(stack)){                            //表达式遍历完毕后，出栈所有元素

insert_key(list,pop(stack));            //并插入存放后缀表达式的链表中

}

free(stack);            //释放栈空间

return list;            //返回后缀表达式

}

根据后缀表达是求运算结果的注释：

点击(此处)折叠或打开

int result(EXP postfix){

EXP stack;

int result=0;

NODE temp = postfix->exp;    //或得表达式

NODE new_node;

NODE number1,number2;

init_expression(&stack); //初始化用来求值时使用的栈

while(temp){                                                //对链表从头到尾行遍历(遍历后缀表达式)

if(temp->type == IS_NUMBER){                            //如果是数字，则创建节点并入栈

new_node = create_node(temp->key,temp->type);        //

push(stack,new_node);                                //

}else{                                                        //    否则为运算符

number1=pop(stack);                                        // 栈中出栈两个运算数

number2=pop(stack);                                        //

result = count(number1->key,number2->key,temp->key);    // 进行相应运算

push(stack,create_node(result,IS_NUMBER));                // 运算结果入栈

}

temp = temp->next;

}

return pop(stack)->key;            //最终栈中存放的即为最终运算结果

}

测试结果如下

第二行给出了后缀表达式

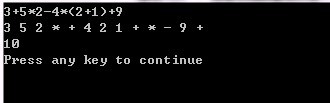
下面是所有代码实现

head.h

点击(此处)折叠或打开

#ifndef HEAD_H_

#define HEAD_H_

typedef int TYPE ;

struct node;        //运算符或数字

struct expression;    //表达式

typedef struct node * NODE;

typedef struct expression *EXP;

void init_expression(EXP *expression);    //初始化表达式

void insert_key(EXP expression,NODE new_node); //链表操作

NODE create_node(int key,TYPE type); //创建一个节点，里面存储的伙食运算符或是数字

void    push(EXP expression,NODE node); //入栈一个运算符或是数字

NODE    get_top(EXP expression);            //或得栈顶元素，不弹出。

NODE    pop(EXP expression);                //或得栈顶元素，弹出

EXP        to_postfix(char *exp);//将普通表达式转换成后缀表达式

int        result(EXP postfix);

void print_list(EXP list); //调试例程

#endif

head.c

点击(此处)折叠或打开

#include

#include

#include"head.h"

#define IS_NUMBER 0

#define IS_OPERATOR 1

enum PRIORITY{level1,level2,level3,level4};

struct node{

long        key;            //运算符或数字

PRIORITY    priority;        //优先级 数字默认设置为1 加减为2 乘除为3 括号为4

TYPE        type;            //区分当前节点中的值是 数字还是 运算符

NODE        next;

};

struct expression{

NODE exp;

NODE last_node;            //因为使用链表作为后缀表达式的存放，每次插入元素都是从尾部插入，为避免每次都要从头遍历到尾部，

//我们设置一个尾部指针,从而使插入操作能立刻完成

};

static int count(int number1,int number2,int ope); //根据运算符运算

static void set_priority(NODE node);    // 设置优先级

static int is_empty(EXP expression);    //判断是否为空

static int tonumber(char c);            //字符到数字的转换

static int is_empty(EXP expression){

return expression->exp==NULL;

}

static void set_priority(NODE node){

switch((char)node->key){

case '(':

case ')':

node->priority = level4;break;

case '*':

case '/':

node->priority = level3;break;

case '+':

case '-':

node->priority = level2;break;

default:

printf("input error! \n");exit(1);break;

}

}

NODE create_node(int key,TYPE type){ //type 区分创建的是一个数字节点还是操作符节点

NODE node = (NODE)malloc(sizeof(struct node));

if(node){

node->key=key;

node->priority=level1; //默认先设置为1

if(type == IS_OPERATOR)

set_priority(node);

node->next = NULL;

node->type = type;

return node;

}else{

printf("malloc error(in create_node)\n");

exit(1);

}

}

void init_expression(EXP *expression){

*expression = (EXP)malloc(sizeof(struct expression));

if(expression == NULL){

printf("initialization expression error!\n");

exit(1);

}

(*expression)->exp = NULL;

(*expression)->last_node = NULL; //为链表设置的表尾指针

}

void insert_key(EXP expression ,NODE new_node){ //插入节点到链表，尾部插入

if(!is_empty(expression)){

expression->last_node->next = new_node;

expression->last_node = new_node;

}else{

expression->exp = new_node;

expression->last_node = new_node;

}

}

void push(EXP expression, NODE new_node){        //入栈

new_node->next = expression->exp;

expression->exp = new_node;

}

NODE get_top(EXP expression){

return expression->exp;

}

NODE pop(EXP expression){            //出栈

NODE temp;

if(!is_empty(expression)){

temp = expression->exp;

expression->exp = temp->next;

}else{

return NULL;

}

return temp;

}

EXP to_postfix(char    *exp){    //求后缀表达式

EXP list;

EXP stack;

init_expression(&list); //初始化用来存放后缀表达式的链表

init_expression(&stack);    //初始化用来得到后缀表达式而是用的栈

NODE temp;

NODE new_node;

NODE top_node;

long key=0;

while(*exp && (*exp)!='\n'){ //开始遍历表达式

if('0' <=*exp && *exp<='9'){                    //这段代码用来提取出像 200 这样不是以为字符表示的数字

while('0' <=*(exp+1) && *(exp+1)<='9'){        //

key =key*10+tonumber(*exp);                //

exp++;                                    //

}                                            //

key =key*10+tonumber(*exp);                    //

new_node=create_node(key,IS_NUMBER);        //创建一个 数字类型的节点 插入链表

insert_key(list,new_node);

key=0;        //重新置0,记录后面的数字

}

else{            //不是数字则是运算符

if(*exp == ')'){                                    //如果碰到的是右括号

NODE local;                                        //则弹出栈元素 直到遇到左括号

while((char)(local=pop(stack))->key !='(' )        // 左右括号丢弃，其他运算符插入链表中(后缀表达式中)

insert_key(list,local);                        //

}else{

new_node=create_node(*exp,IS_OPERATOR);                            //不是右括号，则为一般的运算符

top_node=get_top(stack);                                         //我们尝试或得栈顶元素(不出栈)看优先级是不是小于当前遇到的

if((!top_node) || (top_node->priority < new_node->priority)){    //如果栈空，或者栈顶运算符优先级小于当前运算符

push(stack,new_node);                                        //则当前运算符直接入栈

}else{                                                                //

while(get_top(stack) && get_top(stack)->priority != level4        //

&& (get_top(stack))->priority >= new_node->priority){    //

temp=pop(stack);                                            //否则弹出栈顶元素，并插入链表中(后缀表达式存放的地方)

insert_key(list,temp);                                        //直到栈顶元素优先级小于当前遇到的运算符优先级

}                                                                //注意，除非遇到右括号，否则不能弹出左括号

push(stack,new_node);                                    //最后入栈当前遇到的运算符

}

}

}

exp++;

}

while(get_top(stack)){                            //表达式遍历完毕后，出栈所有元素

insert_key(list,pop(stack));            //并插入存放后缀表达式的链表中

}

free(stack);            //释放栈空间

return list;            //返回后缀表达式

}

static int count(int number1,int number2,int ope){

switch((char)ope){

case '+':

return number1+number2;

case '-':

return number2-number1;

case '*':

return number1*number2;

case '/':

return number1/number2;

}

}

int result(EXP postfix){

EXP stack;

int result=0;

NODE temp = postfix->exp;    //或得表达式

NODE new_node;

NODE number1,number2;

init_expression(&stack); //初始化用来求值时使用的栈

while(temp){                                                //对链表从头到尾行遍历(遍历后缀表达式)

if(temp->type == IS_NUMBER){                            //如果是数字，则创建节点并入栈

new_node = create_node(temp->key,temp->type);        //

push(stack,new_node);                                //

}else{                                                        //    否则为运算符

number1=pop(stack);                                        // 栈中出栈两个运算数

number2=pop(stack);                                        //

result = count(number1->key,number2->key,temp->key);    // 进行相应运算

push(stack,create_node(result,IS_NUMBER));                // 运算结果入栈

}

temp = temp->next;

}

return pop(stack)->key;            //最终栈中存放的即为最终运算结果

}

void print_list(EXP list){

NODE temp = list->exp;

while(temp){

if(temp->type==IS_NUMBER)

printf("%d ",temp->key);

else

printf("%c ",temp->key);

temp = temp->next;

}

printf("\n");

}

int tonumber(char c){

switch(c){

case '0':return 0;

case '1':return 1;

case '2':return 2;

case '3':return 3;

case '4':return 4;

case '5':return 5;

case '6':return 6;

case '7':return 7;

case '8':return 8;

case '9':return 9;

}

}

测试代码

点击(此处)折叠或打开

#include

#include"head.h"

int main(void ){

char s[30];

EXP postfix;

fgets(s,sizeof(s),stdin);

char *exp=s;

postfix=to_postfix(exp);    //得到后缀表达式

print_list(postfix);        //打印后缀表达式

int res=result(postfix);    //根据后缀表达式求结果

printf("%d\n",res);

return 0;

}