费马,法国业余数学家,拥有业余数学之王的称号,费马一生从未受过专门的数学教育,数学研究也不过是业余之爱好。然而,在17世纪的法国还找不到哪位数学家可以与之匹敌:他是解析几何的发明者之一;对于微积分诞生的贡献仅次于牛顿、莱布尼茨,概率论的主要创始人,以及独承17世纪数论天地的人,此外,费马对物理学也有重要贡献。一代数学大师费马堪称是17世纪法国最伟大的数学家,尤其他提出的费马大定理更是困惑了世间智者358年。

费马
所谓的费马点问题就是到三角形三个顶点的距离之和最小的点。费马点结论:对于一个各角不超过120°的三角形,费马点是对各边的张角都是120°的点;对于有一个角超过120°的三角形,费马点就是这个内角的顶点。下面给出几个典型问题,希望大家能够很好地掌握。
1.小颖在学习"两点之间线段最短"查阅资料时发现:△ABC内总存在一点P与三个顶点的连线的夹角相等,此时该点到三个顶点的距离之和最小.
【特例】如图1,点P为等边△ABC的中心,将△ACP绕点A逆时针旋转60°得到△ADE,从而有DE=PC,连接PD得到PD=PA,同时∠APB+∠APD=120°+60°=180°,∠ADP+∠ADE=180°,即B、P、D、E四点共线,故PA+PB+PC=PD+PB+DE=BE.在△ABC中,另取一点P′,易知点P′与三个顶点连线的夹角不相等,可证明B、P′、D′、E四点不共线,所以P′A+P′B+P′C>PA+PB+PC,即点P到三个顶点距离之和最小.
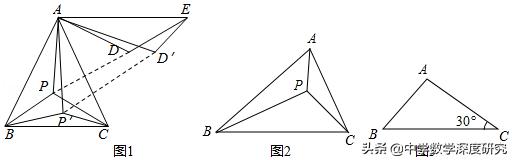
【探究】(1)如图2,P为△ABC内一点,∠APB=∠BPC=120°,证明PA+PB+PC的值最小;
【拓展】(2)如图3,△ABC中,AC=6,BC=8,∠ACB=30°,且点P为△ABC内一点,求点P到三个顶点的距离之和的最小值.
【解析】(1)将△ACP绕点A逆时针旋转60°得到△ADE,可得PC=DE,再证△APD为等边三角形得PA=PD、∠APD=∠ADP=60°,由∠APB=∠BPC=120°知B、P、D、E四点共线,根据两点间线段最短即可得答案;
【点评】本题主要考查旋转变换的性质、全等三角形的判定与性质、等边三角形的判定与性质等知识点,将待求线段的和通过旋转变换及全等三角形的性质转化为同一直线上的线段来求是解题的关键.

2.阅读下列材料:
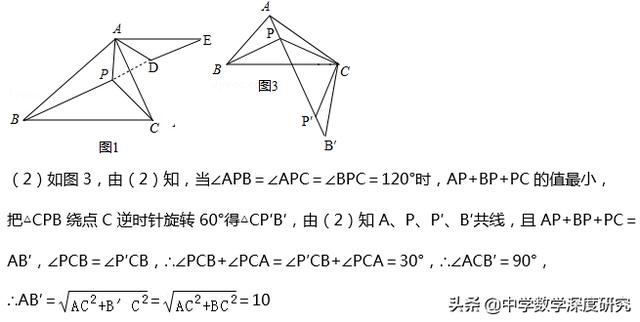
小华遇到这样一个问题,如图1,△ABC中,∠ACB=30°,BC=6,AC=5,在△ABC内部有一点P,连接PA、PB、PC,求PA+PB+PC的最小值.
小华是这样思考的:要解决这个问题,首先应想办法将这三条端点重合于一点的线段分离,然后再将它们连接成一条折线,并让折线的两个端点为定点,这样依据"两点之间,线段最短",就可以求出这三条线段和的最小值了.他先后尝试了翻折、旋转、平移的方法,发现通过旋转可以解决这个问题.他的做法是,如图2,将△APC绕点C顺时针旋转60°,得到△EDC,连接PD、BE,则BE的长即为所求.
(1)请你写出图2中,PA+PB+PC的最小值为 ;
(2)参考小华的思考问题的方法,解决下列问题:
①如图3,菱形ABCD中,∠ABC=60°,在菱形ABCD内部有一点P,请在图3中画出并指明长度等于PA+PB+PC最小值的线段(保留画图痕迹,画出一条即可);
②若①中菱形ABCD的边长为4,请直接写出当PA+PB+PC值最小时PB的长.
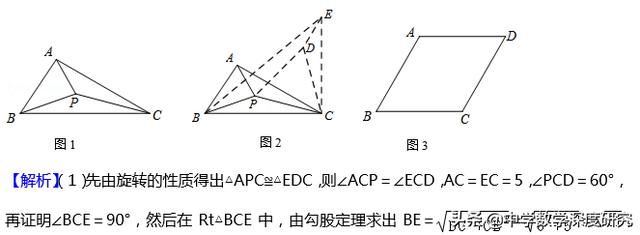
即为PA+PB+PC的最小值;
(2)①将△APC绕点C顺时针旋转60°,得到△DEC,连接PE、DE,则线段BD即为PA+PB+PC最小值的线段;
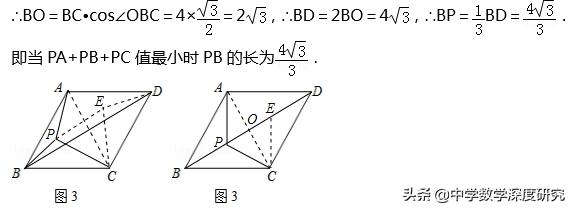
②当B、P、E、D四点共线时,PA+PB+PC值最小,最小值为BD.先由旋转的性质得出△APC≌△DEC,则CP=CE,再证明△PCE是等边三角形,得到PE=CE=CP,然后根据菱形、三角形外角的性质,等腰三角形的判定得出BP=CP,同理,得出DE=CE,则BP=PE=ED=1/3BD.连接AC,交BD于点O,则AC⊥BD.
在Rt△BOC中,∵∠BOC=90°,∠OBC=30°,BC=4,

3.问题提出
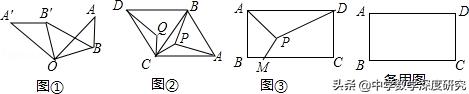
(1)如图①,已知△OAB中,OB=3,将△OAB绕点O逆时针旋转90°得△OA′B′,连接BB′.则BB′=_______ ;
问题探究
(2)如图②,已知△ABC是边长为4√3的等边三角形,以BC为边向外作等边△BCD,P为△ABC内一点,将线段CP绕点C逆时针旋转60°,点P的对应点为点Q.
①求证:△DCQ≌△BCP;
②求PA+PB+PC的最小值;
问题解决
(3)如图③,某货运场为一个矩形场地ABCD,其中AB=500米,AD=800米,顶点A,D为两个出口,现在想在货运广场内建一个货物堆放平台P,在BC边上(含B,C两点)开一个货物入口M,并修建三条专用车道PA,PD,PM.若修建每米专用车道的费用为10000元,当M,P建在何处时,修建专用车道的费用最少?最少费用为多少?(结果保留整数)
【解答】问题提出:(1)由旋转有,∠∠BOB′=90°,OB=3,
根据勾股定理得,BB′=3√2;
问题探究:(2)①∵△BDC是等边三角形,∴CD=CB,∠DCB=60°,
由旋转得,∠PCQ=60°,PC=QC,∴∠DCQ=∠BCP,
在△DCQ和△BCP中, CD=CB, ∠DCQ=∠BCP,CQ=CP,∴△DCQ≌△BCP;
②如图1,连接PQ,∵PC=CQ,∠PCQ=60°,∴△CPQ是等边三角形,
∴PQ=PC,由①有,DQ=PB,∴PA+PB+PC=AP+PQ+QD,
由两点之间线段最短得,AP+PQ+QD≥AD,∴PA+PB+PC≥AD,
∴当点A,P,Q,D在同一条直线上时,PA+PB+PC取最小值为AD的长,
作DE⊥AB,∵△ABC为边长是4√3的等边三角形,
∴CB=AC=4√3,∠BCA=60°,∴CD=CB=4√3,∠DCE=60°,
∴DE=6,∠DAE=∠ADC=30°,∴AD=12,即:PA+PB+PC取最小值为12;
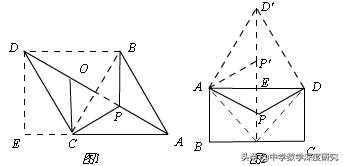
实际应用:(3)如图2,
连接AM,DM,将△ADP绕点A逆时针旋转60°,得△AP′D′,
由(2)知,当M,P,P′,D′在同一条直线上时,AP+PM+DP最小,最小值为D′N,
∵M在BC上,∴当D′M⊥BC时,D′M取最小值,
设D′M交AD于E,∵△ADD′是等边三角形,∴EM=AB=500,
∴BM=400,PM=EM﹣PE=500﹣400√3/3,∴D′E=√3/2AD=400√3,
∴D′M=400√3+500,∴最少费用为10000×(400√3+500)=1000000(4√3+5)万元;
∴M建在BC中点(BM=400米)处,点P在过M且垂直于BC的直线上,且在M上方(500﹣ 400√3/3)米处,最少费用为1000000(4√3+5)万元.

4.(1)知识储备
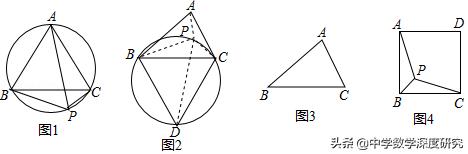
①如图1,已知点P为等边△ABC外接圆的BC上任意一点.求证:PB+PC=PA.
②定义:在△ABC所在平面上存在一点P,使它到三角形三顶点的距离之和最小,则称点P为△ABC的费马点,此时PA+PB+PC的值为△ABC的费马距离.
(2)知识迁移
①我们有如下探寻△ABC(其中∠A,∠B,∠C均小于120°)的费马点和费马距离的方法:
如图2,在△ABC的外部以BC为边长作等边△BCD及其外接圆,根据(1)的结论,易知线段____ 的长度即为△ABC的费马距离.
②在图3中,用不同于图2的方法作出△ABC的费马点P(要求尺规作图).
(3)知识应用
①判断题(正确的打√,错误的打×):
ⅰ.任意三角形的费马点有且只有一个( );
ⅱ.任意三角形的费马点一定在三角形的内部 ( ).
②已知正方形ABCD,P是正方形内部一点,且PA+PB+PC的最小值为√6+√2,
求正方形ABCD的边长.
【解答】(1)①证明:在PA上取一点E,使PE=PC,连接CE,
∵△ABC是等边三角形,∴∠APC=∠ABC=60°,
又∵PE=PC,∴△PEC是正三角形,
∴CE=CP,∠ACB=∠ECP=60°,∴∠ACE=∠BCP,
又∵∠PBC=∠PAC,BC=AC,∴△ACE≌△BCP (ASA),
∴AE=PB,∴PB+PC=AE+PE=AP;
(2)①如图2,得:PA+PB+PC=PA+(PB+PC)=PA+PD,
∴当A、P、D共线时,PA+PB+PC的值最小,
∴线段AD的长度即为△ABC的费马距离;故答案为:AD;
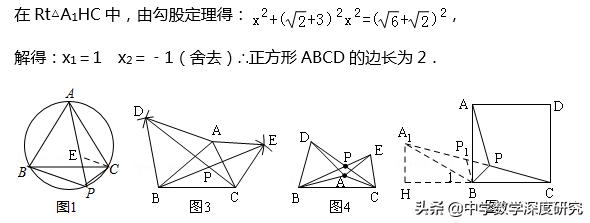
②过AB和AC分别向外作等边三角形,连接CD,BE,交点即为P.(3)①ⅰ.(√);ⅱ.如图4,点P也可以在三角形的外部;(×)
②解:将△ABP沿点B逆时针旋转60°到△A₁BP₁,
如图5,过A₁作A₁H⊥BC,交CB的延长线于H,连接P₁P,
易得:A₁B=AB,PB=P₁B,PA=P₁ A₁,∠P₁BP=∠A₁BA=60°,
∵PB=P₁B,∠P1BP=60°,∴△P₁PB是正三角形,∴PP₁=PB,
∵PA+PB+PC的最小值为√6+√2,∴P₁A₁+PP₁+PC的最小值为√6+√2,
∴A₁,P1,P,C在同一直线上,即A₁C=6+√2,
设正方形的边长为2x,∵∠A1BA=60°,∠CBA=90°,∴∠1=30°,
在Rt△A₁HB中,A₁B=AB=2x,∠1=30°,得:A₁H=x,BH=√3x,

【小结与思考】
通过旋转变换,可以改变线段的位置,优化图形的结构。一般地,当题目出现等腰三角形/等边三角形或正方形条件时,可将图形作旋转60°或90°的几何变换,将不规则图形变为规则图形,或将分散的条件集中在一起,以便挖掘隐含条件,从而解决问题。"费马点"问题实质就是通过旋转将三条共顶点的线段转化在一条折线上,利用"两点之间线段最短"解决。
我们在数学学习过程中,是否需要"模型"?俗话说"成也模式,败也模式",我们掌握一定的模式,能让我们快速找到解决问题的途径。如果死守模式,不会融会贯通,也是"假模式"。我们平时教学中的每一道典型例题都是一种模型,取一个好听的名字只是让学生好记能"顾名思义"。求线段和最短问题,不管是"将军饮马"问题、"胡不归"问题、"阿氏圆"问题,及"费马点"问题,本质都是将折线拉直(将直线同一侧的两条线段转化为直线两侧),再利用"两点之间线段最短"或"垂线段最短"寻找到答案。





















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








