c++ 多重背包状态转移方程_Matlab-自动化控制系统设计7状态空间分析1

本文内容：状态空间方程求解与能控能观性分析

操作环境：matlab2019b

一、状态空间基础

在经典控制理论中，用传递函数来设计和分析单入单出系统，这是一种行之有效的办法。但只能反应系统外部的输入输出关系，不能反应系统内部关系，且需建立在零初始条件下，所以不适用于多变量和时变系统。

在现代控制理论中用状态变量来描述系统，为时变和多变量系统提供了有力的工具。

状态：动力学的状态定义为信息的合集，每一个时刻的状态是唯一确定的

状态变量：能够完全描述系统状态的最小一组变量

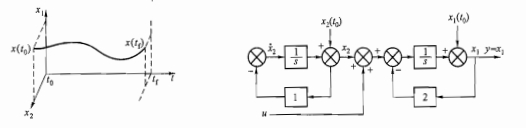
状态向量：如果描述一个给定系统的状态需要n个状态变量，那么这些状态变量可以看成是向量x（t）的各个分量

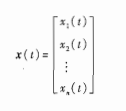
状态空间：以各状态变量作为坐标轴所组成的n维空间叫做状态空间。状态向量则可用空间中的一个点来表示

建立系统的状态空间方程：大家可以参考以下链接，本文主要介绍matlab代码实现就不赘述了

现代控制理论3--系统动态方程的建立_hongliyu_lvliyu的博客-优快云博客​blog.youkuaiyun.com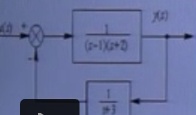

这里介绍matlab中状态空间方程的建立和传递函数与状态空间方程的转换

例：

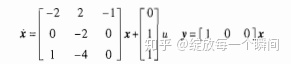
a

把传递函数转换为状态空间：可以用tf2ss或者zp2ss

如零、极点形式：

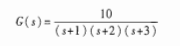
z

二、状态空间方程求解

齐次状态方程：x`=Ax

其解为： x(t)=e^at · x(0)

解法：

方法一：幂级数法（设齐次状态方程的解是t的向量幂级数）

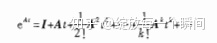
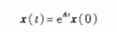
其中e^At，又称为矩阵指数函数/状态转移矩阵

方法二：拉氏变化法

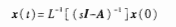
可以发现，两种方法的结果是相同互通的

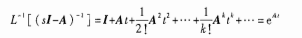
matlab求解：

syms 

求解得

图像为：

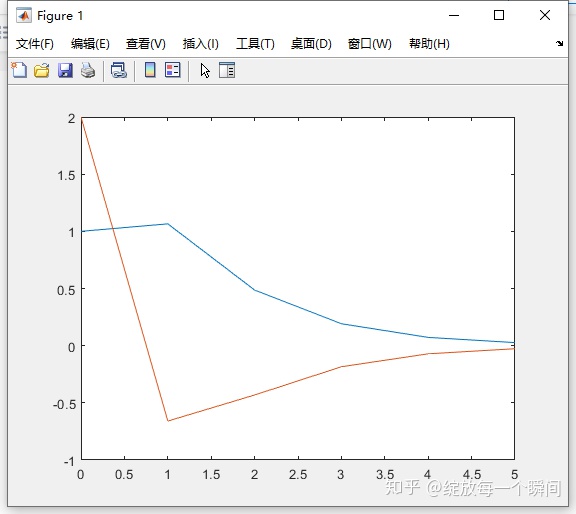
三、线性系统的能控性和能观性

1.能控性与能观性

能控性：一个线性定常系统（A B C）在有限时间间隔t0 ≦ t ≦ tf 内，存在无约束的分段容许连续控制函数 u(t) ，能使系统从任意初态 x(t0)=x0 转移到终态 x(tf)=x1，则称系统是状态完全能控的，简称能控的

能控性判据：

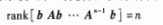
能观性：一个线性定常系统（A B C）在有限时间间隔t0 ≦ t ≦ tf 内，能够根据输出值y(t)和给出的u(t),能够确定系统的初始状态x(t0)的每一个分量，则称系统为完全能观测的，简称不可观测。

能观性判据：

matlab代码实现：

例如判断系列状态方程的能控能观性

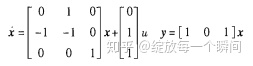
A

可以输出n1=3 ，n2=3，系统能控能观

2.能控（能观）标准型

能控标准型：

一个单输入系统，如果其A，B阵具有以下标准形式：

则系统一定可控

如果系统可控，则一定能找到一个可逆线性变换，将其变化为可控标准型

变化步骤为：

a.由能控性矩阵求逆

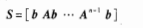
b.得到变换阵P

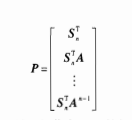
c.进行坐标变换

如：

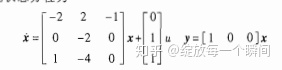
a

能观标准型：

一个单输入系统，如果其A，C阵具有以下标准形式，则系统一定能观

因为能控性系统和能观性系统满足对偶定理,这里不再赘述能观标准型的转换。

本文为小编自行编程，如有错误还请大家批评指出~

待更新~下一篇为“matlab中控制系统的状态空间分析2”