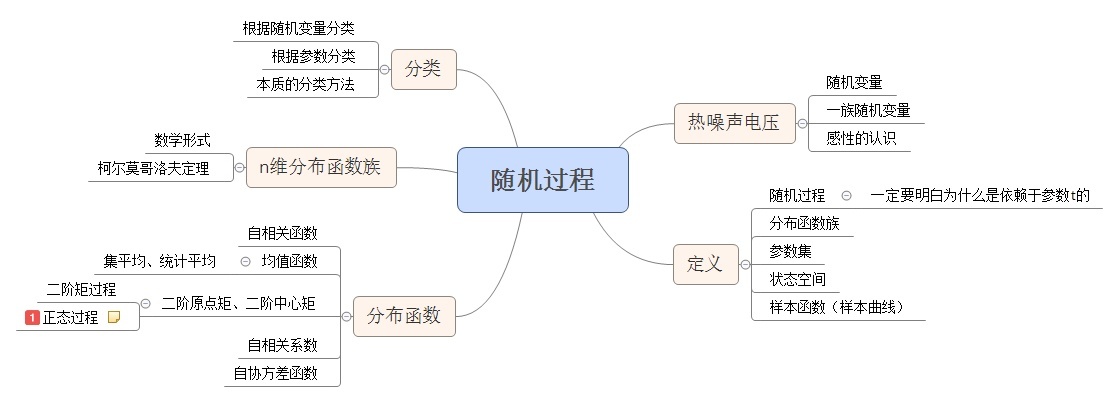
随机过程的自相关函数与功率谱
1. 自相关函数
要说自相关函数,这里得先从统计里的相关函数定义讲起。在统计里,两个随机变量X,Y的相关函数定义如下:
此时,相关函数只是时间差τ=s-t的函数,则公式(2)可以重写为:
这是统计学上的相关函数。
我们把式(4)中期望展开来看,也就是当随机序列有样本时:
上式其实是两个向量的内积表达式,即:
事实上,自相关函数在统计上,反映了同一随机序列在不同时刻取值之间的相关程度。而在信号处理中,一个向量的自相关函数以卷积的形式表达:

要说自相关函数,这里得先从统计里的相关函数定义讲起。在统计里,两个随机变量X,Y的相关函数定义如下:
此时,相关函数只是时间差τ=s-t的函数,则公式(2)可以重写为:
这是统计学上的相关函数。
我们把式(4)中期望展开来看,也就是当随机序列有样本时:
上式其实是两个向量的内积表达式,即:
事实上,自相关函数在统计上,反映了同一随机序列在不同时刻取值之间的相关程度。而在信号处理中,一个向量的自相关函数以卷积的形式表达:

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?


