matlab复数信号_DFT（FFT）结果，采样率，信号频谱的理解

1、因为周期T1信号可以表示为各级高次不同频率的信号（正余弦或者指数）叠加。

但是，我们通常接触的都是数字信号。数字信号是对原始模拟系统采样而得到的。

2、由于采样后得到信号的频谱，是将原始模拟信号的频谱中，低于fs/2的部分和高于fs/2的频谱混叠在一起，而且呈周期出现。因此我们看到的DFT（FFT是其快速计算方法，含义相同）不一定是真实的频谱。只有在采样率高于模拟信号包含频率的最高频率的两倍，我们看到的才是真实的频谱。这个要求采样率高是容易理解。

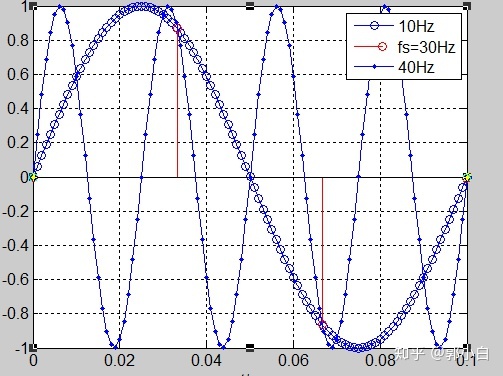
对于上图中，采样率30Hz,而模拟信号f1=10Hz采集的结果，如红色数据。与，模拟信号f2=40hz，采集结果是一样的。当我们只看到AD采集的信号是红色的信号，我们不知道真实的信号是10Hz,还是40Hz的，甚至更高的频率比如f=30*n+10，其中n>1。

因此频率混跌是这样发生的：1、2、3..倍于采样率的信号，采样值是一样的，因此傅里叶频谱看上去也是又回到0频率。高于采样频率的原始信号中的频率，又回到的原点附近，f1-n*fs。其实不是回到了0频率而是叠加到了0频率上，就如同在极坐标中，0度和2

位置一样。后续用Z变换则直接用单位圆表示频谱特性了。