abaqus帮助文档中文版_帮助文档 | ABAQUS SPH方法（中文版）

点击关注，自我充电！ (全文共约6200字) 15.2.1 光滑粒子流体动力学( Smoothed particle hydrodynamics ， SPH ) 适用产品： Abaqus/Explicit 一、概述光滑粒子流体动力学是一种数值方法，属于较大范围的无网格方法的一部分，在这些方法中，用户无需像通常在有限元分析中定义的那样定义节点和单元，取而代之的是，只需要一组点集即可表示给定的体，在光滑粒子流体动力学中，这些点通常称为粒子或伪粒子。图15.2.1–1中的示例对两种方法做了对比，两种离散形式表示都可以模拟瓶子内部流体的初始状态(问题描述详见“Impact of awater-filled bottle,” Section 2.3.2 of the Abaqus Example Problems Guide)。左侧的模型采用传统四面体网格对流体域进行划分，而右侧则采用相同体的离散点集来表示。值得注意的是，在后一种情况下，没有连接节点点的边，因为这些粒子不需要像在传统有限元法一样定义单元。直接定义粒子单元的一种替代方法是：按照常规连续有限元方法定义单元，在分析开始或在分析过程中自动将其转换为粒子单元，详见“Finite elementconversion to SPH particles,” Section 15.2.2所述。

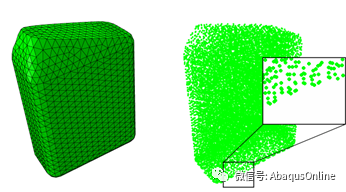
图15.2.1–1 有限元网格和SPH方法粒子分布

光滑粒子流体动力学是一种完全的拉格朗日方法，它可以通过对求解域上的离散点集上直接内插，无需定义空间网格，从而离散一组连续方程组。该方法主要优势是其拉格朗日性质与无固定网格，从而使得与流体流动有关的困难和涉及大变形和自由表面的结构问题以相对自然的方式得到解决。从本质上讲，该方法不是基于离散的粒子在压缩过程中相互碰撞或在拉伸中表现出类似内聚的行为(这种不正确的理解可能源于单词“粒子”)。相反，它只是连续偏微分方程的一种巧妙的离散化方法，在这方面，光滑滑粒子流体动力学与有限元方法非常相似。SPH使用演进的插值方案来近似求解域中任意点的场变量。所感兴趣的粒子上的变量值可以通过对一组相邻粒子的贡献求和来近似，用下标j表示，对于这些粒子， “kernel” 函数W不为零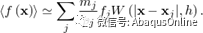

图15.2.1–2给出了 “kernel” 函数的功能。，其中光滑长度h决定有多少粒子影响特定点的插值。

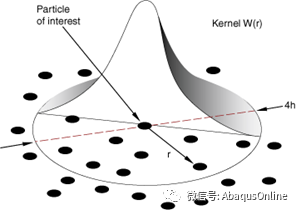
图15.2.1–2 “kernel”函数示意图

自从SPH方法问世以来，它已经获得了实质性的理论支持(Gingoldand Monaghan，1977)，并且与该方法有关的出版物很多。

该方法可使用Abaqus / Explicit中提供的任何材料(包括用户材料)。用户可以像其他任何拉格朗日模型一样指定初始条件和边界条件，还允许与其他拉格朗日体进行接触相互作用，从而扩大了可以使用此方法的应用范围。

当变形不太严重时，该方法的准确性通常不如Lagrangian有限元分析，而在较高变形条件下，此方法的精度不如Eulerian-Lagrangian耦合分析。如果模型中大部分节点与光滑粒子流体动力学相关联，则在使用多个CPU的情况下，分析可能无法很好地扩展。

二、