无向图的深度优先遍历非递归_数据结构-图（图的基本实现C++）

​一、图的概念

图是一种比较复杂的非线性数据结构

图(Graph)是由顶点的有穷非空集合和顶点之间边的集合组成，通常表示为：G(V,E)，其中，G表示一个图，V是图G中顶点的集合，E是图G中边的集合。

图区分有向图和无向图

1、无向图(Undirected graphs)

如果图中任意两个顶点之间的边都是无向边，则称该图为无向图。

无向图相关概念：顶点、边

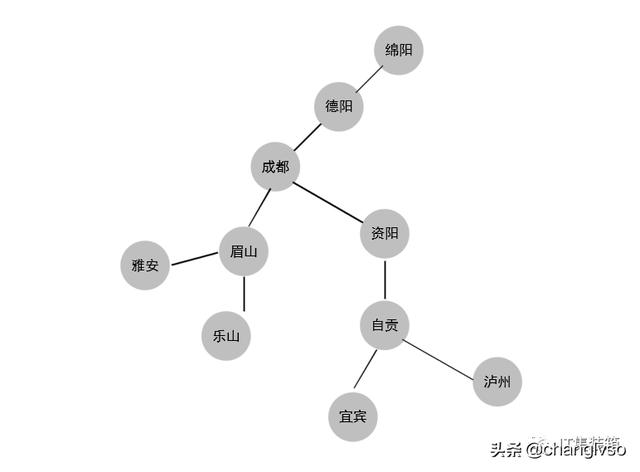
图1-无向图

2、有向图(Directed graphs)

如果图中任意两个顶点之间的边都是有向边，则称该图为有向图

有向图相关概念：顶点、弧(弧头、弧尾 出度、入度)

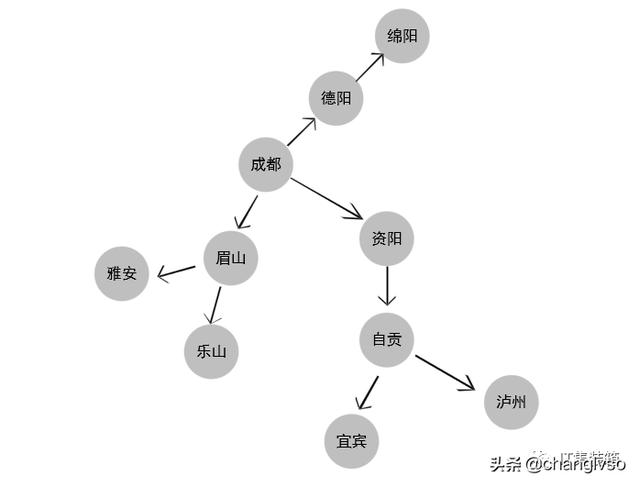
图2-有向图

另外，有些图的边或弧具有与它相关的数值，这种与图的边或弧相关的数值叫做权(Weight)，这是一个求最小生成树的关键值。

二、图的存储

图的存储结构要存储图中的各个顶点本身的信息，以及存储顶点与顶点之间的关系，比较复杂。图的存储结构有邻接矩阵、邻接表、十字链表、邻接多重表等。

三、图的遍历

图的遍历思想是从指定一个顶点出发，开始访问其他顶点，不能重复访问(每个顶点只能访问一次)，直至所有点被访问。

1.深度优先遍历(depth_first_search)

思想：从指定的第一个点开始，沿着向下的顶点不重复的一直遍历下去，若走到尽头，退到上一个顶点，寻找附近有没有顶点，有而且不重复的话，接着遍历，否则退到上一个顶点。

2.广度优先遍历(breadth_first_search)

思想：从指定的第一点开始，先寻找跟它直接相连的所有顶点，然后继续这几个顶点再次深入，每次搜寻的都是同一级别的。

四、最小生成树

1、普利姆(Prim)算法

思路：首先就是从图中的一个起点a开始，把a加入U集合，然后，寻找从与a有关联的边中，权重最小的那条边并且该边的终点b在顶点集合：(V-U)中，我们也把b加入到集合U中，并且输出边(a，b)的信息，这样我们的集合U就有：{a,b}，然后，我们寻找与a关联和b关联的边中，权重最小的那条边并且该边的终点在集合：(V-U)中，我们把c加入到集合U中，并且输出对应的那条边的信息，这样我们的集合U就有：{a,b,c}这三个元素了，一次类推，直到所有顶点都加入到了集合U

2、克鲁斯卡尔(Kruskal)算法

思路：1.将图中的所有边都去掉；2.将边按权值从小到大的顺序添加到图中，保证添加的过程中不会形成环；3.重复上一步直到连接所有顶点，此时就生成了最小生成树。这是一种贪心策略。

终于到了最兴奋的代码时候，代码说明一切！奥利给！

树的邻接矩阵表示法C++基本实现：

#ifndef _CMAP_H_#define _CMAP_H_#include #include #include using namespace std;//顶点class Node{public:Node(char data = 0){m_cData = data;m_bVisited = false;}Node(const Node& node){if (this == &node)return;*this = node;}Node& operator=(const Node& node){if (this == &node)return *this;this->m_cData = node.m_cData;this->m_bVisited = node.m_bVisited;return *this;}public:char m_cData; //数据bool m_bVisited; //是否访问};//边class Edge{public:Edge(int nodeIndexA = 0, int nodeIndexB = 0, int weightValue = 0) :m_iNodeIndexA(nodeIndexA),m_iNodeIndexB(nodeIndexB),m_iWeightValue(weightValue),m_bSelected(false) {}Edge(const Edge& edge){if (this == &edge)return;*this = edge;}Edge& operator=(const Edge& edge){if (this == &edge)return *this;this->m_iNodeIndexA = edge.m_iNodeIndexA;this->m_iNodeIndexB = edge.m_iNodeIndexB;this->m_iWeightValue = edge.m_iWeightValue;this->m_bSelected = edge.m_bSelected;return *this;}public:int m_iNodeIndexA; //头顶点int m_iNodeIndexB; //尾顶点int m_iWeightValue; //权重bool m_bSelected; //是否被选中};//图class CMap{private:int m_iCapacity; //顶点总数int m_iNodeCount; //当前顶点数量Node *m_pNodeArray; //顶点集合int *m_pMatrix; //邻接距阵Edge *m_pEdgeArray; //最小生成树边集合public:CMap(int iCapacity){m_iCapacity = iCapacity;m_iNodeCount = 0;m_pNodeArray = new Node[m_iCapacity];m_pMatrix = new int[m_iCapacity*m_iCapacity];memset(m_pMatrix, 0, m_iCapacity*m_iCapacity * sizeof(int));m_pEdgeArray = new Edge[m_iCapacity - 1];}~CMap(void){delete[]m_pNodeArray;delete[]m_pMatrix;delete[]m_pEdgeArray;}private://广度遍历具体实现void breadthFirstTraverseImpl(vector preVec){int val = 0;vector curVec;for (int i = 0; i < (int)preVec.size(); i++){for (int j = 0; j < m_iCapacity; j++){getValueFromMatrix(preVec[i], j, val);if (/*1 == val*/0 != val){if (m_pNodeArray[j].m_bVisited)continue;cout << m_pNodeArray[j].m_cData << " ";m_pNodeArray[j].m_bVisited = true;curVec.push_back(j);}elsecontinue;}}if (curVec.empty())return;elsebreadthFirstTraverseImpl(curVec);}//取最小边int getMinEdge(const vector& edgeVec){int min = 0, minEdge = 0;for (int i = 0; i < (int)edgeVec.size(); i++){if (edgeVec[i].m_bSelected)continue;min = edgeVec[i].m_iWeightValue;minEdge = i;}for (int i = 0; i < (int)edgeVec.size(); i++){if (edgeVec[i].m_bSelected)continue;if (min > edgeVec[i].m_iWeightValue){min = edgeVec[i].m_iWeightValue;minEdge = i;}}if (0 == min)return -1;return minEdge;}bool isInSet(const vector& nodeSet, int target){for (int i = 0; i < (int)nodeSet.size(); i++){if (nodeSet[i] == target)return true;}return false;}void mergeNodeSet(vector& nodeSetA, const vector& nodeSetB){for (size_t i = 0; i < (int)nodeSetB.size(); i++){nodeSetA.push_back(nodeSetB[i]);}}public://添加顶点void addNode(Node *node){assert(node);m_pNodeArray[m_iNodeCount].m_cData = node->m_cData;m_iNodeCount++;}//将顶点访问设置默认void resetNode(){for (int i = 0; i < m_iNodeCount; i++)m_pNodeArray[i].m_bVisited = false;}//设置权重-有向图bool setValueToMatrixForDirectedGraph(int row, int col, int val = 1){if (row < 0 || row >= m_iCapacity)return false;if (col < 0 || col >= m_iCapacity)return false;m_pMatrix[row*m_iCapacity + col] = val;return true;}//设置权重-无向图bool setValueToMatrixForUndirectedGraph(int row, int col, int val = 1){if (row < 0 || row >= m_iCapacity)return false;if (col < 0 || col >= m_iCapacity)return false;m_pMatrix[row*m_iCapacity + col] = val;m_pMatrix[col*m_iCapacity + row] = val;return true;}//获取权重bool getValueFromMatrix(int row, int col, int& val){if (row < 0 || row >= m_iCapacity)return false;if (col < 0 || col >= m_iCapacity)return false;val = m_pMatrix[row*m_iCapacity + col];return true;}//打印矩阵void printMatrix(){for (int i = 0; i < m_iCapacity; i++){for (int j = 0; j < m_iCapacity; j++)cout << m_pMatrix[i*m_iCapacity + j] << " ";cout << endl;}}//深度遍历void depthFirstTraverse(int index){int val = 0;cout << m_pNodeArray[index].m_cData << " ";m_pNodeArray[index].m_bVisited = true;for (int i = 0; i < m_iCapacity; i++){getValueFromMatrix(index, i, val);if (/*1 == val*/0 != val){if (m_pNodeArray[i].m_bVisited)continue;depthFirstTraverse(i);}elsecontinue;}}//广度遍历void breadthFirstTraverse(int index){cout << m_pNodeArray[index].m_cData << " ";m_pNodeArray[index].m_bVisited = true;vector curVec;curVec.push_back(index);breadthFirstTraverseImpl(curVec);}//求最小生成树-普里斯算法void primTree(int index){int val = 0;int iEdgeCount = 0;vector edgeVec;//待选边集合//从传入点开始找vector nodeIndexVec;nodeIndexVec.push_back(index);//结束条件：边数=顶点数-1while (iEdgeCount < m_iCapacity - 1){//查找传入点的符合要求(权重不为0且目的点没有被访问)边int row = nodeIndexVec.back();cout << m_pNodeArray[row].m_cData << endl;m_pNodeArray[row].m_bVisited = true;for (int i = 0; i < m_iCapacity; i++){getValueFromMatrix(row, i, val);if (0 == val)continue;if (m_pNodeArray[i].m_bVisited)continue;Edge edge(row, i, val);edgeVec.push_back(edge);}//取出最小边int retIndex = getMinEdge(edgeVec);if (-1 != retIndex){//存储选中边edgeVec[retIndex].m_bSelected = true;m_pEdgeArray[iEdgeCount] = edgeVec[retIndex];cout << m_pNodeArray[m_pEdgeArray[iEdgeCount].m_iNodeIndexA].m_cData << " - ";cout << m_pNodeArray[m_pEdgeArray[iEdgeCount].m_iNodeIndexB].m_cData << " (";cout << m_pEdgeArray[iEdgeCount].m_iWeightValue << ") " << endl;iEdgeCount++;int iNodeIndex = edgeVec[retIndex].m_iNodeIndexB;//设置点被访问m_pNodeArray[iNodeIndex].m_bVisited = true;//存入目的点递归查找nodeIndexVec.push_back(iNodeIndex);}}}//最小生成树-克鲁斯卡尔算法void kruskalTree(){int val = 0;int edgeCount = 0;//定义存放节点集合数组vector > nodeSets;//第一步、取出所有边vector edgeVec;for (int i = 0; i < m_iCapacity; i++){for (int j = i + 1; j < m_iCapacity; j++){getValueFromMatrix(i, j, val);if (0 == val)continue;if (m_pNodeArray[i].m_bVisited)continue;Edge edge(i, j, val);edgeVec.push_back(edge);}}//第二步、从所有边中取出组成最小生成树的边//1、算法结束条件：边数=顶点数-1while (edgeCount < m_iCapacity - 1){//2、从边集合中找出最小边int retIndex = getMinEdge(edgeVec);if (-1 != retIndex){edgeVec[retIndex].m_bSelected = true;//3、找出最小边连接点int nodeAIndex = edgeVec[retIndex].m_iNodeIndexA;int nodeBIndex = edgeVec[retIndex].m_iNodeIndexB;//4、找出点所在集合bool nodeAInSet = false;bool nodeBInSet = false;int nodeAInSetLabel = -1;int nodeBInSetLabel = -1;for (int i = 0; i < (int)nodeSets.size(); i++){nodeAInSet = isInSet(nodeSets[i], nodeAIndex);if (nodeAInSet)nodeAInSetLabel = i;}for (int i = 0; i < (int)nodeSets.size(); i++){nodeBInSet = isInSet(nodeSets[i], nodeBIndex);if (nodeBInSet)nodeBInSetLabel = i;}//5、根据点集合的不同做不同处理if (nodeAInSetLabel == -1 && nodeBInSetLabel == -1){vector vec;vec.push_back(nodeAIndex);vec.push_back(nodeBIndex);nodeSets.push_back(vec);}else if (nodeAInSetLabel == -1 && nodeBInSetLabel != -1){nodeSets[nodeBInSetLabel].push_back(nodeAIndex);}else if (nodeAInSetLabel != -1 && nodeBInSetLabel == -1){nodeSets[nodeAInSetLabel].push_back(nodeBIndex);}else if (-1 != nodeAInSetLabel && -1 != nodeBInSetLabel && nodeAInSetLabel != nodeBInSetLabel){//mergeNodeSet(nodeSets[nodeAInSetLabel], nodeSets[nodeBInSetLabel]);nodeSets[nodeAInSetLabel].insert(nodeSets[nodeAInSetLabel].end(),nodeSets[nodeBInSetLabel].begin(),nodeSets[nodeBInSetLabel].end());for (int k = nodeBInSetLabel; k < (int)nodeSets.size() - 1; k++){nodeSets[k] = nodeSets[k + 1];}}else if (nodeAInSetLabel != -1 && nodeBInSetLabel != -1 && nodeAInSetLabel == nodeBInSetLabel){continue;}m_pEdgeArray[edgeCount] = edgeVec[retIndex];edgeCount++;cout << m_pNodeArray[edgeVec[retIndex].m_iNodeIndexA].m_cData << " - ";cout << m_pNodeArray[edgeVec[retIndex].m_iNodeIndexB].m_cData << " (";cout << edgeVec[retIndex].m_iWeightValue << ") " << endl;}}}};#endif // !_CMAP_H_

测试图结构：

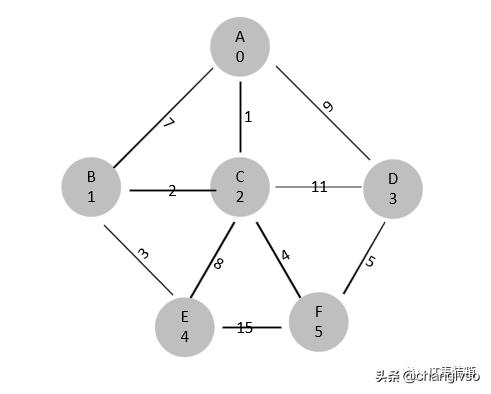
图3-测试图结构

测试函数main.cpp：

#include "CMap.hpp"#include using namespace std;int main(int argc, char**argv){CMap *pMap = new CMap(6);Node *pNodeA = new Node('A');Node *pNodeB = new Node('B');Node *pNodeC = new Node('C');Node *pNodeD = new Node('D');Node *pNodeE = new Node('E');Node *pNodeF = new Node('F');pMap->addNode(pNodeA);pMap->addNode(pNodeB);pMap->addNode(pNodeC);pMap->addNode(pNodeD);pMap->addNode(pNodeE);pMap->addNode(pNodeF);pMap->setValueToMatrixForUndirectedGraph(0, 1, 7);pMap->setValueToMatrixForUndirectedGraph(0, 2, 1);pMap->setValueToMatrixForUndirectedGraph(0, 3, 9);pMap->setValueToMatrixForUndirectedGraph(1, 2, 2);pMap->setValueToMatrixForUndirectedGraph(1, 4, 3);pMap->setValueToMatrixForUndirectedGraph(2, 3, 11);pMap->setValueToMatrixForUndirectedGraph(2, 4, 8);pMap->setValueToMatrixForUndirectedGraph(2, 5, 4);pMap->setValueToMatrixForUndirectedGraph(3, 5, 5);pMap->setValueToMatrixForUndirectedGraph(4, 5, 15);cout << "打印矩阵: " << endl;pMap->printMatrix();cout << endl;pMap->resetNode();cout << "深度优先遍历: " << endl;pMap->depthFirstTraverse(0);cout << endl;pMap->resetNode();cout << "广度优先遍历: " << endl;pMap->breadthFirstTraverse(0);cout << endl;pMap->resetNode();cout << "普里姆算法: " << endl;pMap->primTree(0);cout << endl;pMap->resetNode();cout << "克鲁斯卡尔算法: " << endl;pMap->kruskalTree();cout << endl;pMap->resetNode();system("pause");return 0;}

执行结果：

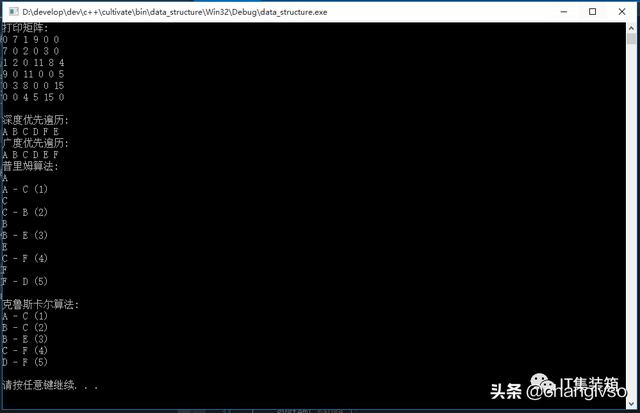
图4-执行结果

--|END|--