本文介绍了使用Time-Dependent Cox比例风险模型分析用户流失的步骤，涉及生存曲线KM估计、PH假设检验和Extended Cox模型。通过Python的lifeline和R的survival&survminer库进行实现。生存分析结合用户流失研究，能深入理解用户行为和风险因子，同时解决删失数据问题。
一分钟读完全文
介绍了Time-Dependent 生存模型应用于用户流失的主要建模步骤，主要包括生存曲线KM估计，PH假设检验，含有Time-Dependent系数与Time-Dependent协变量的Extended Cox PH Model建模。主要借助python中的lifeline和R中的survival&survminer包实现。
用户流失建模与生存分析
生存分析最初用于对病人服药后的存活时长进行拟合与风险因素分析，并因可解决censored data而被广泛采纳。随后，生存分析逐渐被利用于各种与duration有关的问题中，并成为了最著名的time-to-event模型之一。另一方面，用户流失是用户行为中的一个主要研究方向。随着机器学习的大热，许多机器学习模型如RF/SVM/NN都被应用于对用户流失的预测。但大部分预测都在做分类，即判断一个用户会不会流失，而非在做duration。如果把survival model引入进来做用户流失，可以解决两方面的问题，第一，可以研究duration，第二，对风险因子具有强解释性。
生存分析实际可以划分为两大块，生存曲线的拟合和风险因子的建模。第一块非常简单，利用Kaplan-Meier (KM) estimate对曲线进行估计即可；第二块本身也不难，但如果引入了时变效果，数据操作难度就相应增加了。Terry Therneau（R包survival的作者）在18年11月发表了 Using Time Dependent Covariates and Time Dependent Coefficients in the Cox Model，对如何处理时变因素做了非常好的讲解。本文也主要基于该文思路进行展开。
一个完整的生存分析可归纳为：
- 原始数据格式处理：把数据处理为用户、生存时长、是否删失的数据格式。
- KM估计及生存曲线的绘制。
- 判断协变量是否存在时变变量，如果有，进行数据格式的二次处理，将数据打断为用户、起始时间、结束时间、是否删失的格式。
- 判断协变量系数是否存在时变效果，即著名的PH假设检验。如果检验不通过，对时变效果进行绘制，并基于绘制结果进行数据分层（stratify）。
- 建立Extended Cox PH Model，对风险因子进行影响估计。
下面将逐步进行展开。
生存曲线估计
在介绍生存曲线之前，需要介绍一个概念叫“censored”删失。删失的意思很好理解，就是这个用户我不知道他啥时候流失的。比如说我在2018年第一天开始对N个用户进行观测，到最后一天结束。在这一年里，有K个用户流失了，有N-K个用户到最后一天还没流失。这时我们在计算每个用户的生存时长时，对于流失掉的K个用户，我们是可以计算的，但对于没有流失的N-K个用户，我们由于并不知道他们啥时候流失，我们计算出来的生存时长实际是偏小的，这些用户，我们称为“censored observation”或者“unobserved data”。censored还可以进一步分为left censor/right censor/inter censor，具体可以搜索，这里不做过多讨论。
在绘制生存曲线时，需要有一列来专门对每个用户是否censored进行标记。另外一列则是duration。我们在python里面的lifeline包中演示一下（R一样可以做，我只是习惯用py了）：
from lifelines import KaplanMeierFitter
import matplotlib.pyplot as plt
plt.rcParams["font.family"] = "Times New Roman"
plt.rcParams.update({'font.size':12})
kmf = KaplanMeierFitter()
T = agg_use_coup_final["duration_s"]
E = agg_use_coup_final["observed"] # 0: unobserved, right censored; 1: observed, churn.
kmf.fit(T, event_observed=E)
kmf.plot(show_censors=True, censor_styles={'ms': 2, 'marker': 'x'}, color='k')
plt.legend(['Censored data', 'Kaplan-Meier Estimate', 'Confidence interval'])输出图片如下：
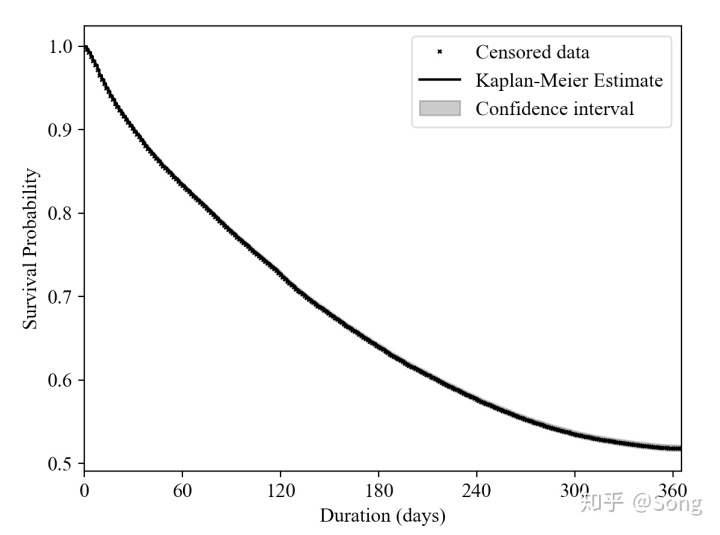
我们这个数据量很大，所以看censored data以及置信区间看得不是很清楚。拟合出曲线后，我们可以计算一些指标，比如中位流失时间等等。同时，如果没有时变因子，现有数据带上需要分析的协变量，就已经可以进行传统的COX PH建模了：
import lifelines
from lifelines import CoxPHFitter
cph = CoxPHFitter()
cph.fit(agg_use_coup_final, duration_col='duration_s', event_col='observed', show_progress=True)
# cph.plot_covariate_groups('Total_Number', range(0, 100, 10))
cph.print_summary() # access the results using cph.summary时变协变量处理
时变协变量是没有检验来检测的，需要自己判断。一个典型的例子就是多疗程治疗下用户的死亡时间，如果以用户接受的药剂量来做协变量，则属于一个经典时变变量。因为用户活得越久，接受大疗程越多，注入的要药剂也越多。换而言之，药剂量在用户的生存期内，是随时间变化的，不像性别这些因素一样保持不变。这样的问题在用户流失中同样存在，如优惠券的累计发放量，同样与药剂量类似。
对于这种变量，我们需要对原始数据做split。根据变化的时间节点，把原始数据打断为多行。以用户流失为例，假设某用户在一年内35日、186日、303日分别接受了优惠券：
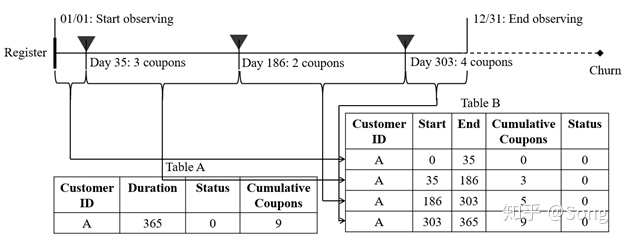
我们需要把数据格式从TABLE A变成TABLE B。在操作层面，可以借助lifeline中的to_long_format和add_covariate_to_timeline来完成：
import lifelines
from lifelines.utils import to_long_format
from lifelines.utils import add_covariate_to_timeline
from lifelines import CoxTimeVaryingFitter
# 构建两个矩阵：BASE矩阵与拆分矩阵
# BASE矩阵：存有每个用户的起终点时间
base_df = to_long_format(agg_use_coup_final, duration_col='duration_s')
# 拆分矩阵：记录的是在该时刻变量发生了变化。
# 比如，base_df中用户A的start为0，stop为10。sin_coupon_inf中用户的time为5，说明用户在5时优惠券信息发生了变化。
df = add_covariate_to_timeline(base_df, sin_coupon_inf, duration_col='time', id_col='authid_s', event_col='observed')时变系数处理
时变系数表示的是该变量对用户的影响随时间变化，比如某药剂对病人的疗效，会随着时间变长而逐渐减弱。对于这一类变化的判断，需要借助统计检验工具。自此之后我们切换到R的survival包来完成：
library(survival)
library(ggplot2)
library(dplyr)
library(ggfortify)
library(survminer)
#read raw data
dat <-
read.csv('/Users/husonghua/Desktop/EV+MONEY/data/0109agg_use_coup.csv')
dat$observed <- as.integer(dat$observed)
dat$observed <-
dat$observed - 1 # 1:the death was observed,0:thw survival time was censored
str(dat)
#timevarying cox model
cox_split <-
coxph(
Surv(start, stop, observed) ~ age + sexf + cumvalue + cumusecoup + coup_durt +
Count_bus + Count_metro +
Count_ev + near_bus + near_metro + near_price + Is_college +
Is_hub + LUM + Pop_density + Job_density +
cluster(authid_s),
data = dat
)
#TEST the PROPORTIONAL HAZARDS
zph0 <- cox.zph(cox_split)
ggcoxzph(zph0[4])
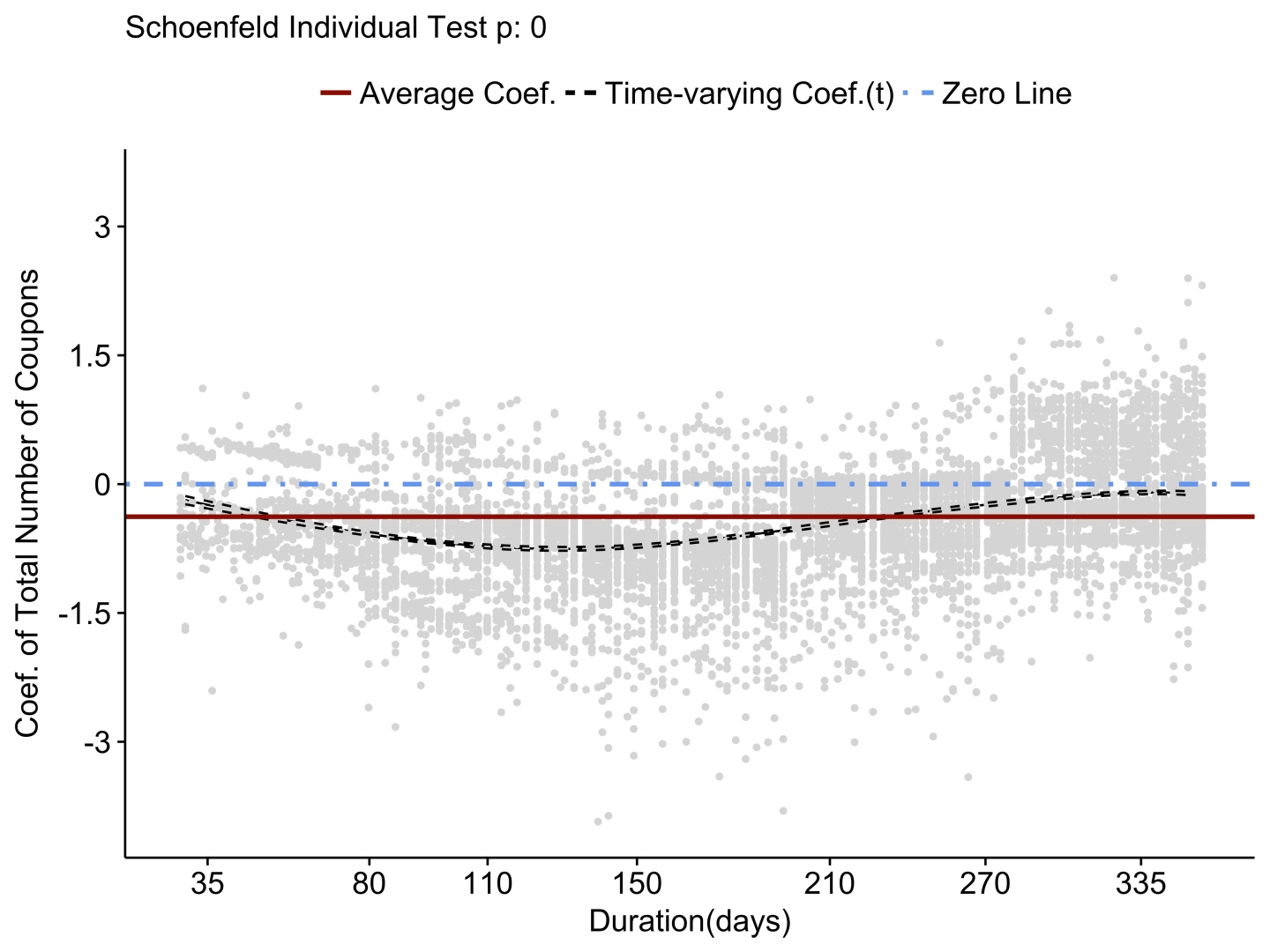
检测思路是先进行time-varying cox 的建模（注意此时的建模与传统额COX已经不同了，需要输入start stop observed三列），然后对模型进行cox.zph检测，检测结果中，P值越小，说明系数随时变效果越明显。举个例子，下图是一个检测结果，coupon的P值非常小，可以认为存在一个显著的时变系数。
最后对变化明显的系数进行时变图绘制。注意我们采用了survminer包来加强绘制效果（ggcoxzph）。此包的出图好过survival包的出图，同时还可以进行很多参数的修改：
ggcoxzph(
resid = T,#是否绘制点
zph0[4],
point.col = 'gray83',#点的颜色
df = 7,#曲线的自由度
nsmo = 100,
ggtheme = theme_survminer(#字体大小及主题设置
base_size = 14,
font.main = c(14, "plain", "black"),
font.submain = c(14, "plain", "black"),
font.x = c(14, "plain", "black"),
font.y = c(14, "plain", "black"),
font.caption = c(14, "plain", "black"),
font.tickslab = c(14, "plain", "black"),
legend = c("top"),
font.legend = c(14, "plain", "black")
)
)
ggsave(
'/Users/Desktop/5.png',
width = 8,
height = 6,
dpi = 1000
)
最后的出图效果：
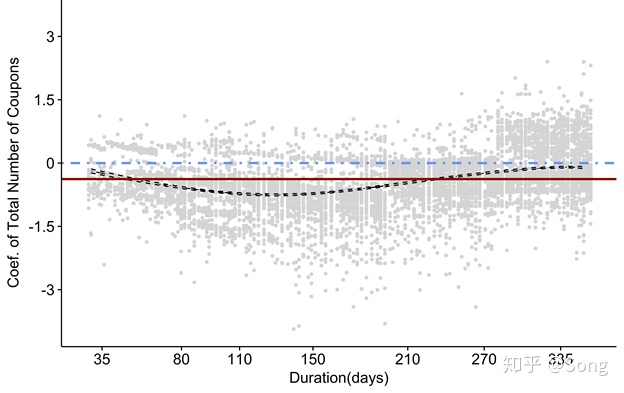
其中黑色曲线为影响系数随时间的变化拟合曲线，而棕色则是传统的比例COX模型的拟合结果。可见随时间变化明显，不能采用简单的比例COX模型建模。
如何解决这一类问题呢，Terry Therneau给出了几种办法，最简单的就是做分层（stratify），根据图形中的时变效果，进行阶段划分。比如这里我们根据130这个时间点，将数据划分为两个group，最后再重新拟合：
# 根据时间变化进行组的拆分
dat$tgroup <- 2
dat[dat$stop < 130, 'tgroup'] <- 1
# 重新拟合
cox_split1 <-
coxph(
Surv(start, stop, observed) ~ age + sexf + coup_durt + Count_bus + Count_metro +
cumvalue +
Count_ev + near_bus + near_metro + near_price + Is_college +
Is_hub + LUM + Pop_density + Job_density +
cluster(authid_s) + cumusecoup:strata(tgroup),
data = dat
)
#zph1 <- cox.zph(cox_split1)
summary(cox_split1)
注意此时多加了一项cumusecoup:strata(tgroup)，用于表示分层拟合。
结果解释
最终的COX模型结果输出都是类似的，主要需要看三列，第一列为系数，如果为正，则表示会增大风险，为负则减小风险。第二列为比值，即使风险（hazard rate）系数增大或减小的倍数，最后则是看P值，表示是否显著（这个解释和对logit model做解释很像，hazard rate类似于odds ratio，都是对系数做exp）。
举个例子，下图为一个原始的COX模型结果，可见优惠券的数量（total_number）可以明显的降低用户流失风险，且每增加一个优惠券，风险会变为原来的0.94倍。
至此，一个完整的生存模型完成了。
参考文献
Analyzing Customer Churn - Cox Regression
https://cran.r-project.org/web/packages/survival/vignettes/timedep.pdf
lifelines - lifelines 0.19.2 documentation
扫一扫
1078
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
