c语言分解质因数法求最大公约数,最大公约数求法大全

原标题：最大公约数求法大全

小复习

上一次我们介绍了一种特殊的最大公约数求法，叫做辗转相除法。你还记得吗？

辗转相除法

用较小数除较大数，再用出现的余数(第一余数)去除除数，再用出现的余数(第二余数)去除第一余数，如此反复，直到最后余数是0为止。如果是求两个数的最大公约数，那么最后的除数就是这两个数的最大公约数。

那么，今天我们就对最大公约数求法做一个总结噢。

最大公约数求法汇总

1、质因数分解法

思路：把每个数分别分解质因数，再把各数中的全部公有质因数提取出来连乘，所得的积就是这几个数的最大公约数。

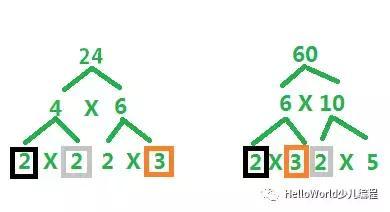
举例：假设我们求24和60的最大公约数。

第一步：分解24和60。

24=2X2X2X3

60=2X3X2X5

第二步：24和60的最大公约数=24和60共有的公因子相乘，即2X2X3=12。

2、短除法

思路：短除法求最大公约数，先用这几个数的公约数连续去除，一直除到所有的商互质为止，然后把所有的除数连乘起来，所得的积就是这几个数的最大公约数。

短除法的本质就是质因数分解法，只是将质因数分解用短除符号来进行。

举例：

12的因数有：1、2、3、4、6、12。

18的因数有：1、2、3、6、9、18。

12与18的公因数有：1、2、3、6。

12与18的最大公因数是6。

3、更相减损法

思路：

第一步：任意给定两个正整数；判断它们是否都是偶数。若是，则用2约简；若不是则执行第二步。

第二步：以较大的数减较小的数，接着把所得的差与较小的数比较，并以大数减小数。继续这个操作，直到所得的减数和差相等为止。

则第一步中约掉的若干个2与第二步中等数的乘积就是所求的最大公约数。

举例：

用更相减损术求98与63的最大公约数。

由于63不是偶数，把98和63以大数减小数，并辗转相减：

98-63=35

63-35=28

35-28=7

28-7=21

21-7=14

14-7=7

所以，98和63的最大公约数等于7。

代码实现：

4、辗转相除法

辗转相除法在之前的文章中有详细介绍噢！

这么多求法你掌握了几种呢~返回搜狐，查看更多

责任编辑：