c语言非递归实现二叉树的遍历算法,C语言 二叉树的遍历 递归和（多种）非递归算法...

于 2021-05-23 23:32:00 发布
阅读量431 收藏 1
点赞数
文章标签： c语言非递归实现二叉树的遍历算法

//二叉树遍历

//作者：nuaazdh

//时间：2011年12月1日

#include

#include

#define OK 1

#define ERROR 0

#define TRUE 1

#define FALSE 0

#define OVERFLOW -1

#define STACK_INIT_SIZE 100

#define STACKINCREMENT 10

typedef int Status;

typedef char ElemType; // 二叉树结点元素类型

typedef struct BiTNode{ // 二叉树结点结构

char data; // 结点数据

struct BiTNode *lchild; // 左孩子

struct BiTNode *rchild; // 右孩子

}BiTNode,*BiTree;

typedef BiTree SElemType;

typedef struct{//栈结构定义

SElemType *base;

SElemType *top;

int stacksize;

}SqStack;

Status InitStack(SqStack *S);

//构造一个空栈S

Status DestroyStack(SqStack *S);

//销毁栈S，S不再存在

Status ClearStack(SqStack *S);

//把栈S置为空栈

Status StackEmpty(SqStack S);

//若栈S为空栈，则返回TRUE，否则返回FALSE

int StackLength(SqStack S);

//返回S元素的个数，即栈的长度

Status GetTop(SqStack S,SElemType *e);

//若栈不为空，则用e返回S的栈顶元素，并返回OK；否则返回FALSE

Status Push(SqStack *S,SElemType e);

//插入元素e为新的栈顶元素

Status Pop(SqStack *S,SElemType *e);

//若栈S不为空，则删除S的栈顶元素，用e返回其值，并返回OK,否则返回ERROR

Status StackTraverse(const SqStack *S);

//从栈底到栈顶依次对每个元素进行访问

BiTree CreateBiTree(BiTree T);

// 按先后次序输入二叉树中结点的值(一个字符)，空格表示空树

// 构造二叉链表表示的二叉树T

Status PreOrderRecursionTraverse(BiTree T,Status (*Visit)(ElemType e));

// 采用二叉链表存储结结构，Visit是对数据元素操作的应用函数

// 先序遍历二叉树T的递归算法，对每个数据元素调用函数Visit

Status InOrderRecursionTraverse(BiTree T,Status (*Visit)(ElemType e));

// 采用二叉链表存储结结构，Visit是对数据元素操作的应用函数

// 中序遍历二叉树T的递归算法，对每个数据元素调用函数Visit

Status PostOrderRecursionTraverse(BiTree T,Status (*Visit)(ElemType e));

// 采用二叉链表存储结结构，Visit是对数据元素操作的应用函数

// 后序遍历二叉树T的递归算法，对每个数据元素调用函数Visit

Status PreOrderNonRecursionTraverse(BiTree T,Status (*Visit)(ElemType e));

// 采用二叉链表存储结结构，Visit是对数据元素操作的应用函数

// 先序遍历二叉树T的非递归算法，对每个数据元素调用函数Visit

Status InOrderNonRecursionTraverse(BiTree T,Status (*Visit)(ElemType e));

// 采用二叉链表存储结结构，Visit是对数据元素操作的应用函数

// 中序遍历二叉树T的非递归算法，对每个数据元素调用函数Visit

Status PostOrderNonRecursionTraverse(BiTree T,Status (*Visit)(ElemType e));

// 采用二叉链表存储结结构，Visit是对数据元素操作的应用函数

// 后序遍历二叉树T的非递归算法，对每个数据元素调用函数Visit

Status Visit(ElemType e);

// 对二叉树中的数据元素访问

int main()

{

BiTree T=NULL;

Status(*visit)(ElemType e)=Visit;

printf("请按先序遍历输入二叉树元素(每个结点一个字符，空结点为'#'):\n");

T=CreateBiTree(T);

printf("\n递归先序遍历：\n");

PreOrderRecursionTraverse(T,visit);

printf("\n递归中序遍历：\n");

InOrderRecursionTraverse(T,visit);

printf("\n递归后序遍历：\n");

PostOrderRecursionTraverse(T,visit);

printf("\n非递归先序遍历：\n");

PreOrderNonRecursionTraverse(T,visit);

printf("\n非递归中序遍历：\n");

InOrderNonRecursionTraverse(T,visit);

printf("\n非递归后序遍历：\n");

PostOrderNonRecursionTraverse(T,visit);

printf("\nEnd of main.\n");

return 0;

}

BiTree CreateBiTree(BiTree T){

// 按先后次序输入二叉树中结点的值(一个字符)，空格表示空树

// 构造二叉链表表示的二叉树T

char ch;

scanf("%c",&ch);

if(ch=='#') T=NULL;

else{

if(!(T=(BiTNode *)malloc(sizeof(BiTNode))))

exit(OVERFLOW);

T->data=ch; // 生成根节点

T->lchild=CreateBiTree(T->lchild); // 构造左子树

T->rchild=CreateBiTree(T->rchild); // 构造右子树

}

return T;

}

Status PreOrderRecursionTraverse(BiTree T,Status (*Visit)(ElemType e))

{ // 先序遍历递归算法

if(T){

if(!Visit(T->data)) return ERROR;

PreOrderRecursionTraverse(T->lchild,Visit);

PreOrderRecursionTraverse(T->rchild,Visit);

}

return OK;

}

Status InOrderRecursionTraverse(BiTree T,Status (*Visit)(ElemType e))

{ // 中序遍历递归算法

if(T){

InOrderRecursionTraverse(T->lchild,Visit);

if(!Visit(T->data)) return ERROR;;

InOrderRecursionTraverse(T->rchild,Visit);

}

return OK;

}

Status PostOrderRecursionTraverse(BiTree T,Status (*Visit)(ElemType e))

{ //后序遍历递归算法

if(T){

PostOrderRecursionTraverse(T->lchild,Visit);

PostOrderRecursionTraverse(T->rchild,Visit);

if(!Visit(T->data)) return ERROR;;

}

return OK;

}

Status PreOrderNonRecursionTraverse(BiTree T,Status (*Visit)(ElemType e)){

// 先序遍历二叉树T的非递归算法

SqStack S;

SElemType p;

InitStack(&S); Push(&S,T); // 根指针入栈

while(!StackEmpty(S)){

Pop(&S,&p);//访问根节点

if(!Visit(p->data)) return ERROR;

if (p->rchild)

Push(&S,p->rchild);

if(p->lchild)

Push(&S,p->lchild);

}//while

DestroyStack(&S);

return OK;

}

/**算法一

Status InOrderNonRecursionTraverse(BiTree T,Status (*Visit)(ElemType e)){

// 中序遍历二叉树T的非递归算法

SqStack S;

SElemType p;

InitStack(&S); Push(&S,T); // 根指针入栈

while(!StackEmpty(S)){

while(GetTop(S,&p)&&p) Push(&S,p->lchild); //向左走到尽头

Pop(&S,&p); //空指针出栈

if(!StackEmpty(S)){//访问结点，向右一步

Pop(&S,&p);

if(!Visit(p->data)) return ERROR;

Push(&S,p->rchild);

}//if

}//while

DestroyStack(&S);

return OK;

}

*/

Status InOrderNonRecursionTraverse(BiTree T,Status (*Visit)(ElemType e)){

// 中序遍历二叉树T的非递归算法

SqStack S;

SElemType p;

InitStack(&S); p=T;

while (p||!StackEmpty(S)){

if (p){

Push(&S,p);p=p->lchild;//根指针进栈，遍历左子树

}else{//根指针退栈，访问根节点，遍历右子树

Pop(&S,&p);if(!Visit(p->data))return ERROR;

p=p->rchild;

}//else

}//while

DestroyStack(&S);

return OK;

}

/**算法一

Status PostOrderNonRecursionTraverse(BiTree T,Status (*Visit)(ElemType e)){

// 后序遍历二叉树T的非递归算法

SqStack S;

SElemType p,q;

InitStack(&S); Push(&S,T); // 根指针入栈

while(!StackEmpty(S)){

while(GetTop(S,&p)&&p&&(p->lchild||p->rchild)){

Push(&S,p->rchild);// 右子树入栈

Push(&S,p->lchild);// 左子树入栈

}//注意栈中存在空指针，表示某个结点的右子树为空

if(!StackEmpty(S)){//访问结点

Pop(&S,&p);

if (p){

if(!Visit(p->data)) return ERROR;

}else{// 存在右子树为空的结点，继续向上返回

Pop(&S,&p);

if(!Visit(p->data)) return ERROR;

}

while (GetTop(S,&q)&&q&&p==q->rchild){//若当前为右子树，则继续出栈

Pop(&S,&p);

if(!Visit(p->data)) return ERROR;

GetTop(S,&q);

}

}//if

}//while

DestroyStack(&S);

return OK;

}

*/

/***算法二*/

Status PostOrderNonRecursionTraverse(BiTree T,Status (*Visit)(ElemType e)){

// 后序遍历二叉树T的非递归算法

SqStack S;

SElemType p,q;

InitStack(&S); Push(&S,T); // 根指针入栈

while(!StackEmpty(S)){

while(GetTop(S,&p)&&p) Push(&S,p->lchild); //向左走到尽头

Pop(&S,&p); //空指针出栈

GetTop(S,&p);

if(p->rchild){

Push(&S,p->rchild);

continue;

}

if(!StackEmpty(S)){//访问结点，向右一步

Pop(&S,&p);

if(!Visit(p->data)) return ERROR;

while (GetTop(S,&q)&&q&&p==q->rchild){//若当前为右子树，则继续出栈

Pop(&S,&p);

if(!Visit(p->data)) return ERROR;

}

GetTop(S,&p);

if(p->rchild){

Push(&S,p->rchild);

continue;

}else{

Pop(&S,&p);

if(!Visit(p->data)) return ERROR;

}

}//if

}//while

DestroyStack(&S);

return OK;

}

Status Visit(ElemType e){

// 对二叉树中的数据元素访问

if(e=='\0'){

return ERROR;

}else{

printf("%c",e);

}

return OK;

}

//-----------顺序栈操作--------------//

Status InitStack(SqStack *S){

//构造一个空栈S

S->base=(SElemType *)malloc(STACK_INIT_SIZE*sizeof(SElemType));

if(!S->base)//分配失败

{

printf("分配内存失败.\n");

exit(0);

}

S->top=S->base;

S->stacksize=STACK_INIT_SIZE;

return OK;

}

Status DestroyStack(SqStack *S){

//销毁栈S，S不再存在

if(!S)//S为空

{

printf("指针为空，释放失败.\n");

exit(0);

}

free(S->base);

return OK;

}

Status ClearStack(SqStack *S){

//把栈S置为空栈

if(!S)//S不存在

return FALSE;

S->top=S->base;//直接将栈顶指针指向栈底

return OK;

}

Status StackEmpty(SqStack S){

//若栈S为空栈，则返回TRUE，否则返回FALSE

if(S.top==S.base)

return TRUE;

else

return FALSE;

}

int StackLength(SqStack S){

//返回S元素的个数，即栈的长度

return S.stacksize;

}

Status GetTop(SqStack S,SElemType *e){

//若栈不为空，则用e返回S的栈顶元素，并返回OK；否则返回FALSE

if(S.top==S.base){

return FALSE;

}else{

*e=*(S.top-1);

return OK;

}

}

Status Push(SqStack *S,SElemType e){

//插入元素e为新的栈顶元素

if(S->top-S->base>=S->stacksize){//栈已满，追加存储空间

S->base=(SElemType *)realloc(S->base,(S->stacksize+STACKINCREMENT)*sizeof(SElemType));

if(!S->base)

{

printf("重新申请空间失败.\n");

exit(0);

}

S->top=S->base+S->stacksize;//更改栈顶指针

S->stacksize+=STACKINCREMENT;

}

*S->top++=e;

return OK;

}

Status Pop(SqStack *S,SElemType *e){

//若栈S不为空，则删除S的栈顶元素，用e返回其值，并返回OK,否则返回ERROR

if(S->top==S->base){//栈为空

return ERROR;

}

*e=*(--S->top);

return OK;

}

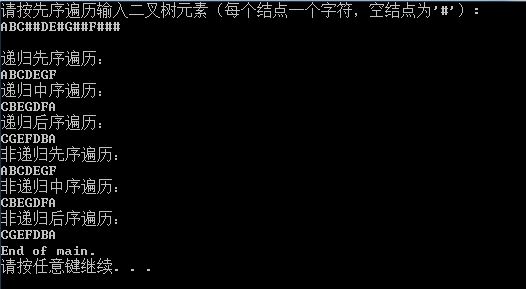
运行结果：

121d2be29ef2e872f5019b7d6d59b996.png

评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值