最大似然法监督分类步骤_阿尔茨海默病多模态分类的流形正则化多任务特征选择...

摘要：

准确诊断阿尔茨海默病及其前驱期(即轻度认知障碍)对疾病的早期治疗非常重要。最近，多模态方法已经用于融合来自多个不同且互补的成像和非成像模态的信息。尽管有许多现有的多模态方法，但是很少有人能够从通常用于分类的多模态数据中联合识别与疾病相关的大脑区域的问题。本文提出了一种流形正则化多任务学习框架，用于从多模态数据中联合选择特征。

具体来说，我们将多模态分类表述为一个多任务学习框架，其中每个任务侧重于基于每个模态的分类。为了捕捉多个任务(即模态)之间的内在关联性，我们采用了一种组稀疏正则化器，该正则化器只保证少量特征被联合选择。此外，我们引入了一个新的基于流形的拉普拉斯正则化项来保持每个任务的原始数据的几何分布，这可以导致选择更多的判别特征。此外，我们将我们的方法扩展到半监督设置，这是非常重要的，因为获取大量标记数据(即疾病诊断)通常是昂贵和耗时的，而收集未标记数据相对容易得多。为了验证我们的方法，我们对阿尔茨海默病神经成像计划(ADNI)数据库的基线磁共振成像(磁共振成像)和氟脱氧葡萄糖正电子发射断层扫描(FDG-正电子发射断层扫描)数据进行了广泛的评估。实验结果证明了该方法的有效性。

介绍：

阿尔茨海默病是最常见的痴呆类型，占年龄相关性痴呆病例的 60-80%。据预测，受影响的人数将在未来 20 年翻一番，到 2050 年，每 85 人中就有 1 人受影响。由于特定的大脑变化在患者出现症状前几年就开始了，因此早期临床诊断成为一项具有挑战性的任务。

最近，机器学习和模式分类方法已被广泛用于阿尔茨海默病和轻度认知障碍的神经影像分析，包括群体比较(即临床不同群体之间)和个体分类。早期的研究主要集中在从单一成像模态中提取特征(例如，基于感兴趣区域或基于体素)，如结构磁共振成像或氟脱氧葡萄糖正电子发射断层扫描等。最近，研究人员开始整合多种成像模式，以进一步提高疾病诊断的准确性。

不同的成像方式提供了大脑功能或结构的不同视图。例如，结构性核磁共振成像提供了关于大脑组织类型的信息，而功能性磁共振成像则测量葡萄糖的大脑代谢率。直观地说，多模态的集成可以揭示以前隐藏的信息，这些信息不能通过使用单一模态来找到。

一些特征选择技术已经被用于从多模态数据中识别疾病相关区域，而这些技术的明显缺点是它们没有考虑不同模态之间的特征之间的内在相关性。据我们所知，只有少数几项研究从多模态神经影像数据中联合选择特征用于阿尔茨海默病/轻度认知障碍分类。例如，黄等人提出利用稀疏复合线性判别分析(SCLDA)方法从多模态数据中联合识别与疾病相关的脑特征。张等人提出了一种用于广告分类的多模态多任务学习联合特征选择方法，并在广告分类中取得了最新的成绩。

在本文中，我们提出了一种新的基于多任务的联合特征选择模型，该模型同时考虑了多模态数据之间的内在关联性和各模态数据的几何分布。为此，我们将多模态数据的分类表述为多任务学习(MTL)问题，其中每个任务侧重于每种形态的分类。MTL 的目标是通过联合学习一组相关任务来提高泛化性能。具体来说，在所提出的模型中包括两个正则化项。第一个项目是组套索正则化器，它确保在不同的任务(即模态)中只联合选择少量的特征。第二项是拉普拉斯正则化项，它可以保留每个任务的整个数据的几何分布信息。这些信息可能有助于捕捉更多的辨别特征。此外，我们将我们的方法扩展到半监督设置(即，从标记和未标记的数据中学习)，这在实践中非常重要，因为标记数据的获取(即，疾病的诊断)通常是昂贵和耗时的，而未标记数据的收集相对容易得多。

流形正则化多任务特征选择：

我们首先简要介绍现有的多任务特征选择方法。然后，我们推导了我们提出的流形正则化多任务特征选择模型以及相应的优化算法。

多任务特征选择(MTFS)

假设有 M 个监督学习任务(即，模态的数量)，多任务特征选择(MTFS)模型求解以下目标函数:

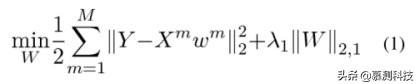
其中 W 是权重矩阵，其行 wj 是与不同任务的第 j 个特征相关联的系数向量。这里，

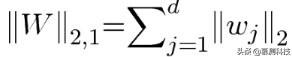
是矩阵 w 的行的 ℓ2-norms 的和，如在套索组[7]中使用的。ℓ2,1-norm 的使用鼓励了许多零行矩阵。换句话说，这种 ℓ2,1-norm 组合了多个任务，并确保在不同的任务中选择少量的共同特征。参数 λ1 是平衡两个项的相对贡献的正则化参数。

流形正则化多任务特征选择：

在 MTFS 模型中，采用线性映射函数将数据从原始高维空间转换到一维空间。在这个模型中，对于每个任务，我们只考虑数据和类标签之间的关系，而忽略了数据之间的相互依赖性，这可能导致映射后即使是非常相似的数据也有很大的偏差。

为了解决这个问题，我们引入了一个新的正则化项，它保留了整个数据的几何分布信息:

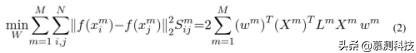
其中 S 表示相似性矩阵，该矩阵定义了不同主题之间任务 m 的相似性。

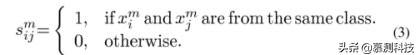
流形正则化多任务特征选择模型具有以下目标函数:

半监督 M2TFS：

一般而言，半监督学习方法试图利用未标记数据所揭示的内在数据分布，从而有助于构建更好的学习模型。很容易发现，在所提出的 M2TFS 模型中，只有等式中的第一项和相似性矩阵 S 涉及监督信息(即主题的类别标签)，因此我们可以很容易地将我们的模型扩展到半监督版本

我们首先定义一个对角矩阵 P ∈ R^(N×N)来表示已标记的数据，然后我们用下面的高斯函数重新定义相似矩阵 Sm：

最后，基于等式(4)我们的半监督 M2TFS 模型(表示为半 M2TFS)的目标函数可以写成如下:

最优化算法

优化等式 6 中的问题，我们利用了广泛应用的加速近端梯度(APG)方法。在本文中，我们实现了一个 APG 优化过程。具体来说，我们首先在等式中分离目标函数。(6)中光滑部分:

和非光滑部分:

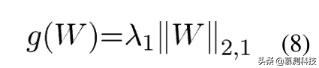
然后，构造以下函数来逼近复合函数 f(W) + g(W):

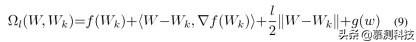
最后，AGP 算法的更新步骤定义为:

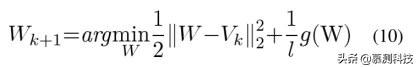
AGP 算法的关键是如何有效地解决更新步骤。文献的研究表明，这个问题可以分解成 d 个独立的子问题，并且这些子问题的解析解很容易得到。此外，根据其他文献中使用的技术，我们可以计算以下公式，而不是基于 Wk 进行梯度下降:

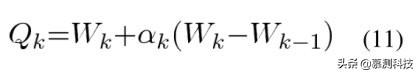
分类：

之后，我们采用了基于多核的支持向量机(SVM)方法进行分类。具体地，对于训练对象的每个模态，首先基于由上述提出的方法选择的特征来计算线性核。然后，采用多核 SVM 对多模态数据进行组合分类。

实验:

为了评估我们提出的方法的有效性，我们对来自阿尔茨海默氏病神经成像倡议(ADNI)数据库的多模态数据进行了一系列实验。我们总共使用了 202 名受试者，其具有相应的基线磁共振成像和正电子发射断层扫描数据，包括 51 名阿尔茨海默病患者、99 名轻度认知障碍患者(包括 43 名轻度认知障碍转换者和 56 名轻度认知障碍非转换者)和 52 名正常对照者。

为了评估所提出方法的性能，我们采用分类精度、接收器工作特性曲线下面积、灵敏度(即正确预测的患者比例)和特异性(即正确预测的正常对照比例)作为性能度量。分别对 202 个 ADNI 基线磁共振成像和正电子发射断层扫描数据进行了两组实验，即监督分类和半监督分类。在这两组实验中，分别建立了多个二进制分类器，即模数转换器与数控转换器、微通道转换器与数控转换器、微通道转换器与微通道非转换器。

有监督分类：

在当前的研究中，我们将我们提出的方法与基于多模态的最先进的方法进行了比较，包括其他文献中提出的多模态方法(分别对应于“无特征选择”和“套索作为特征选择”)和多任务特征选择方法(表示为 MTFS)。此外，为了进行更多的比较，我们还将磁共振成像和 FDG-正电子发射断层扫描的所有特征连接成一个长特征向量，然后执行两种不同的特征选择方法，即 t 检验、套索和顺序向前浮动选择(SFFS) 。最后，使用具有线性核的标准 SVM 进行分类。

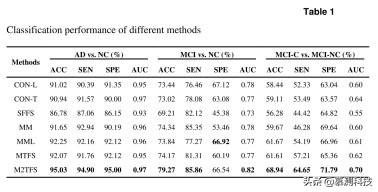
表 1 中可以看出，我们提出的 M2TFS 方法在三个分类组上始终优于其他方法。具体而言，我们提出的 M2TFS 方法对阿尔茨海默病和非阿尔茨海默病、轻度认知障碍和轻度认知障碍的分类准确率分别为 95.03%、79.27%和 68.94%，而其他方法的最佳分类准确率分别为 92.25%、74.34%和 61.67%。

半监督分类：

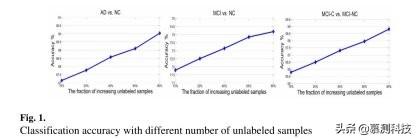
在实验中，我们验证了我们提出的方法在半监督设置下的分类性能。具体来说，我们首先将阳性和阴性受试者的比率 r1 =50%固定为标记数据。在以下程序中，我们使用其余受试者的分数 R2∑{ 10%、20%、40%、60%、80%}作为未标记数据。

图 1 显示了我们提出的方法在使用不同数量的未标记样本时的分类精度。从图 1 中可以看出，随着三个分类组上未标记样本的增加，分类精度可以得到一致的提高，这表明所提出的方法可以通过使用数据的几何分布来选择更具区别性的特征，因此分类性能随着未标记数据数量的增加而显著提高。这些结果也证明了通过添加数据的分布信息所获得的显著增益。

结论：

本文提出了利用数据的几何分布来建立多任务特征选择方法，以从多模态数据中联合选择特征。通过在多任务中引入流形正则化项，使用加速邻近梯度算法来寻找最优解，以找出信息量最大的特征子集。针对监督和半监督两种情况，我们提出了流形正则化多任务特征选择方法，相应的算法分别称为 M2TFS 和半 M2TFS。在 ADNI 数据集上的实验结果验证了该方法的有效性。与现有的多任务特征选择方法不同，该方法利用数据的几何分布知识对阿尔茨海默病进行早期诊断，效果更好。

致谢

本文由南京大学软件学院 2020 级博士生尹伊宁翻译转述