canvas 绘制直线 并选中_WebGL 直线直吗？

前言

如题，”直线直吗“？当思考这个问题时，我们回过头想想之前的文章所讲的直线是由什么组成的：WebGL 中图元有点、线和三角形，虽然三者都被定义为最基础的图形，但它们之间也有着密不可分的联系，正如《酒干倘卖无》中唱到的：”没有点哪有线“ 直线段便是由许多像素点组成的图形。

我们知道像素点其实是正方形的，那么如果展示的直线是水平或者垂直于水平方向的，那么像素点的排列也必然是沿水平或垂直于水平方向的，那么此时直线必然是直的。以俄罗斯方块距离，此时的直线应该是对应俄罗斯方块中的这图形：

但大多数情况下直线并不是严格水平或竖直的，那么这种情况下，我们看到的直线更像是下面这些图形的排列组合：

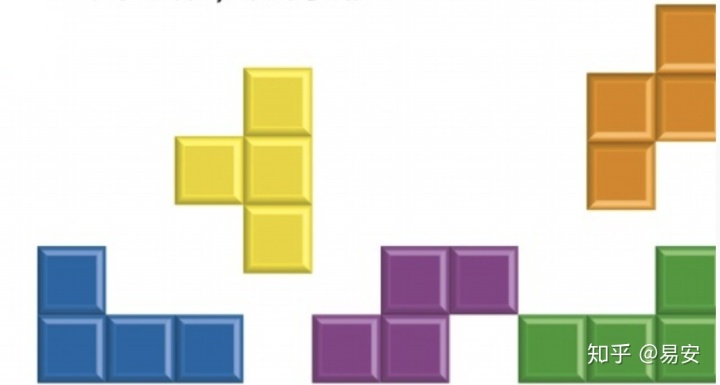
那这些像素点是以何规则排布的呢？就此引出我们今天的主题——直线段的扫描转换算法

直线段的扫描转换算法

在之前将 WebGL 工作流程时我们提到过一个环节叫做 光栅化，比较标准地解释是确定最佳逼近图形的像素集合，并用指定属性写像素的过程称为光栅化或图形的扫描转换。

听懂没？没？说白了就是把图像转化为像素点的过程。

本篇主要介绍三种直线段光栅化的算法：数值微分法、中点画线法和 Bresenham算法。

数值微分法

数值微分法（DDA） 也称为 离散插值分析法 （本文统称为数值分析法）。

大家都知道在坐标系中可以用

来表示一条直线，那么当我们知道了我们要绘制线段的端点

后，即可通过

两点式 求出其所在直线的表达式：

，从而再转换成

的形式。

分别就是点在屏幕上的坐标，假设

从

开始，每次绘制向

端点移动距离为1像素，那么我们要求的下一个点

：

这样我们就把求要绘制点的算法简化成了一个加法。同时，对屏幕而言，像素点的坐标值并没有小数一说所以需要对所求得的

值进行四舍五入处理。代码如下：

// vertex shader

let 

效果如图：

注意，该算法仅适用于

的情况，当

时，需要将

互换，即

增加1，

对应增加

。

中点画线法

假如当前绘制的点是

，则当在绘制下一个点时我们实际上有两种选择：

和

。若

为

的中点，

为理想直线与直线

的交点。则当

在

下方时，

应为下一个像素点；否则，

应为下一个像素点。这就是

中点画线法 的原理，如下图：

我们将直线方程标准化后可以得到：

的形式，其中

，同时点与直线的有如下关系：

因此，只需将点

带入

即可判断中点

与直线的关系。后续绘制就没什么两样了。

Bresenham 算法

该算法与中点画线法类似，只不过在此算法中定义了一个 误差项

，

并不是一个固定值，而是随着顶点的改变而变化的。误差项初始值为0，

下标每增加1，

的值相应增加直线的斜率值

，即

。而要绘制顶点的位置与误差项

关系如下：

• 时，直线与
  相交的点最接近于当前像素
  的右上方像素
  ；
• 时，交点更接近于当前像素右侧的像素
  ；

注意，假如下一个要绘制的点为右上方的像素时，因为我们选取了新的

方向的基准点，故

要减1。

结束语

总结一下三种直线段扫描算法的原理：

1. 数值微分法：使用
   ，求
   ，并四舍五入得到下一个要绘制的像素；
2. 中点画线法：如果中点在理想直线与
   交点的上方，则绘制右侧像素，反之绘制右上方像素；
3. Bresenham 算法：如果误差项
   ，则绘制右上方像素，反之绘制右侧像素。

这就是计算机如何绘制的直线，简简单单，不知和你想象中是否一致？我们在反过头看文章开篇的问题 “直线是直的吗”，或许你自己心中也有了答案！

大家可以看到上面图片中的直线有锯齿，这是因为像素逼近有误差，会使图形发生畸变，这种现象称为 走样。当然也有解决这种问题的技术方法，而这些技术则就称为 反走样，比如最粗暴的方法就是提高分辨率，同时还有 区域采样、加权区域采样 等方式。感兴趣的小伙伴可以自行了解

感谢阅读，欢迎关注公众号：Refactor！