点到直线的投影公式_射影法求异面直线之间的距离

特定方法对应特定题型，方法不是万能，灵活才是王道。

异面直线之间的距离不是高考中明确要求要考的内容，课本上也没有对应的内容，但与立体几何有关的最值问题中却经常出现，在一些难度中上的高二立体几何同步课测试中也会出现，求异面直线距离的方法较多，罗列如下：

1.定义法，找公垂线

2.建系，用向量求

3.转化法，线线距离转化为线面距离或面面距离

4.等体积转化法，也是转化法中的一种，单独归为一类是因为很重要也最常用，以后会单独出一篇关于等体积转化法的内容。

5.公式法，太复杂，记不住

6.极值法，原理是异面直线之间公垂线最短，用函数的思想去解，属于知道就可以型。

7.射影法，还算不错的方法，简单易懂

今天说到的射影法用到了上面的转化法，若异面直线a,b，其中b∈平面β，且a//β，则a到平面β的距离即为所求异面直线距离，若a∈平面α，b∈平面β，且α//β，则两平面之间的距离即为所求异面直线的距离。看下图：

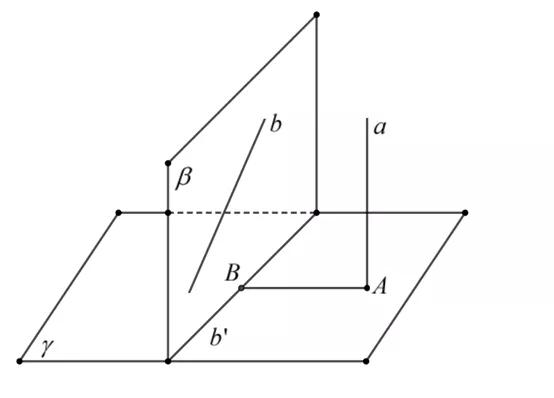
如上图所示，若异面直线a,b在平面γ中的射影分别为点A和直线b'，则点A到直线b'的距离即为异面直线的距离，从点A作AB⊥b'，B为垂足，则AB即为异面直线之间的距离。

证明过程很简单，直线a在平面γ上的射影为一点A，可知直线a⊥平面γ，若直线b不在平面γ上，且直线b在平面γ上的射影为b'，则直线b和b'可确定一个平面β，且平面β⊥平面γ，因此直线a//平面β，AB即为直线a与平面β的公切线，因此AB也为异面直线a,b之间的距离。

我们知道一条直线在另一个平面内的投影是一个点或一条线，若两条异面直线在同一个平面的投影为两条平行的直线，那么平行线之间的距离即为异面直线之间的距离，证明方法和上述类似，也可参照正方体来辅助理解，在此不提。

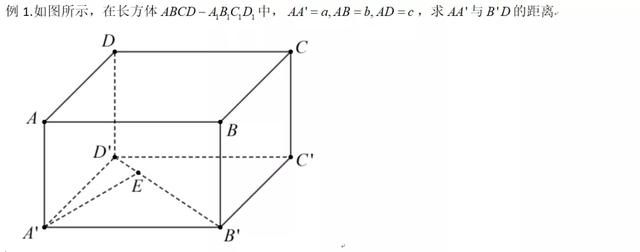
将异面直线AA'和B'D投射到底面A'B'C'D'上分别为点A'和B'D'，从A'向B'D'作垂线，垂足为E，则A'E的长度即为异面直线之间的距离。

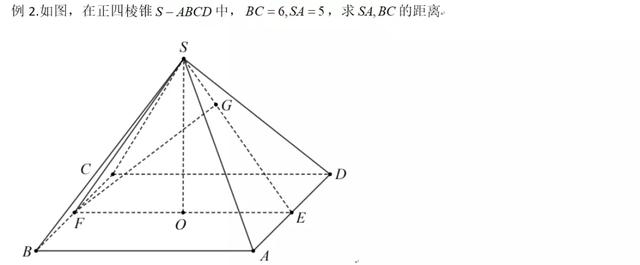
平面外的一条直线只要不与平面垂直，投影都会是一条直线，只有当直线与平面垂直时投影才是一个点，因此需要找到与两条异面直线其中之一垂直的平面即可，然后把立体几何转化为平面几何来解即可。

题目中为正四棱锥，因此取BC，AD的中点与S构成一个平面，这个平面与BC垂直，BC和SA在平面SEF上的投影分别为点F和SE，因此只需要求出点F到直线SE之间的距离即可。

以上两个题目需要用的投影平面要么几何体中本来就有的平面，或者很容易通过辅助线找到的平面，若所需的平面不是很容易作时，这种方法的优势就不见得有多强了，但话又说回来，不规则的几何体在高考中也不会出现，即便是不规则的几何体在高考中也能切割成若干个规则几何体的组合体，在今年4月24号发的2020年太原理科一模中有一个这样的题目，当时的解法是：

如下图，将BF放到平面AEF中，此时AC//平面BEF,异面直线的距离即为点A到平面BEF的距离，用等体积法求高即可：

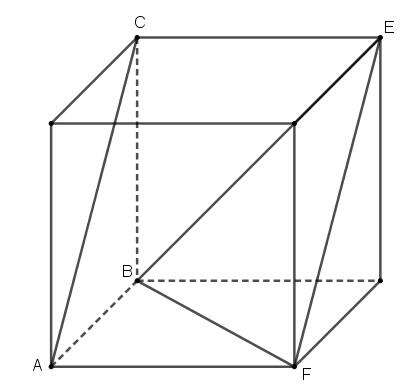
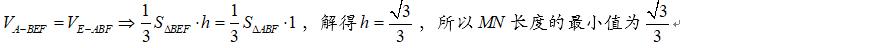
如果用射影法，先找到一个与AC或BF垂直的平面，显然与BF垂直的平面很容易找，与AC垂直的平面就跑到外面去了，作辅助线如下图：

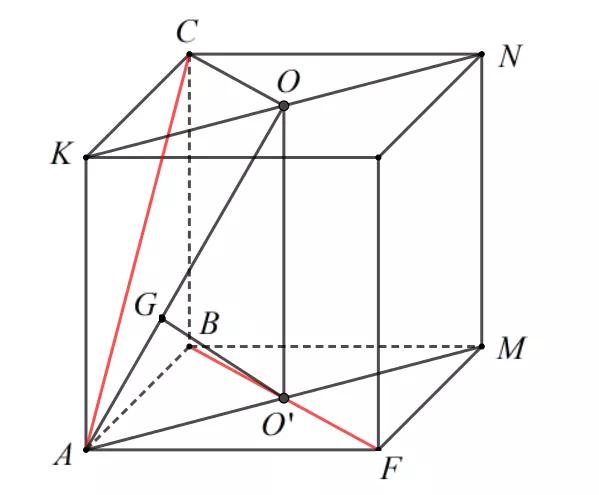
可知与BF垂直的平面为平面AMNK，BF和AC在平面AMNK上的射影分别为O'和AO，在直角△AOO'中，异面直线AC和BF的距离即为从O'点出发到AO边上的高线长度,因为OO'=1,AO'=√2/2,AO=√6/2,可求得O'G=√3/3

同学们可把本题目的两种做法做一个对比，显然射影法更简单直接一些。

综上所述：射影法求异面直线间的距离是常用方法的一种补充，对特定题目还是比较有效果的，但亦非通用方法，射影法不仅仅用在这里，在求二面角夹角余弦值和异面直线夹角时同样能用到，是和射影定理，三垂线定理，三垂面定义同样实用的几何方法，希望同学们给以重视。