支持向量机训练集多少个_支持向量机（原理）

最新推荐文章于 2025-06-02 18:39:57 发布

weixin_39702479

最新推荐文章于 2025-06-02 18:39:57 发布

阅读量1.1k

点赞数

文章标签：支持向量机训练集多少个支持向量机鸢尾花代码

本文详细介绍了支持向量机(SVM)的基本原理及其在不同场景下的应用。包括SVM的数学基础、分类间隔、硬间隔与软间隔的概念，以及如何通过核函数处理非线性问题。此外，还探讨了SVM在多分类问题中的解决方案。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

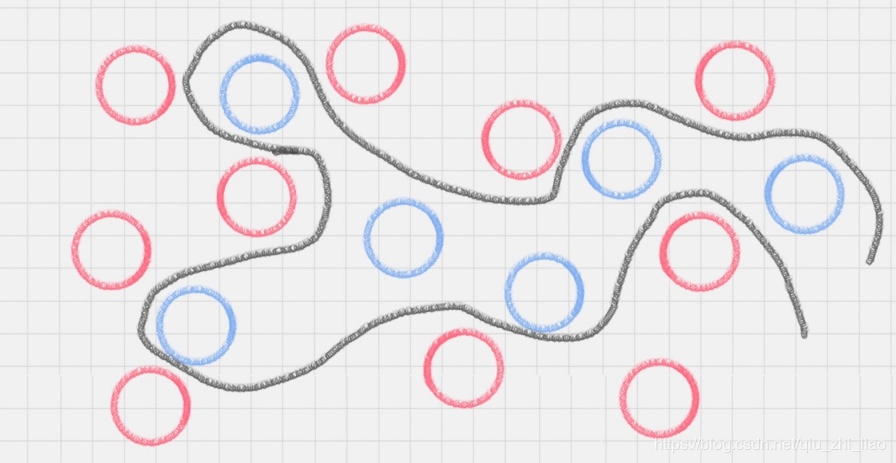
SVM 的英文叫 Support Vector Machine，中文名为支持向量机。它是常见的一种分类方法，在机器学习中，SVM 是有监督的学习模型。

什么是有监督的学习模型呢？它指的是我们需要事先对数据打上分类标签，这样机器就知道这个数据属于哪个分类。同样无监督学习，就是数据没有被打上分类标签，这可能是因为我们不具备先验的知识，或者打标签的成本很高。所以我们需要机器代我们部分完成这个工作，比如将数据进行聚类，方便后续人工对每个类进行分析。
SVM 作为有监督的学习模型，通常可以帮我们模式识别、分类以及回归分析。

先看一张图，明白超平面的概念：

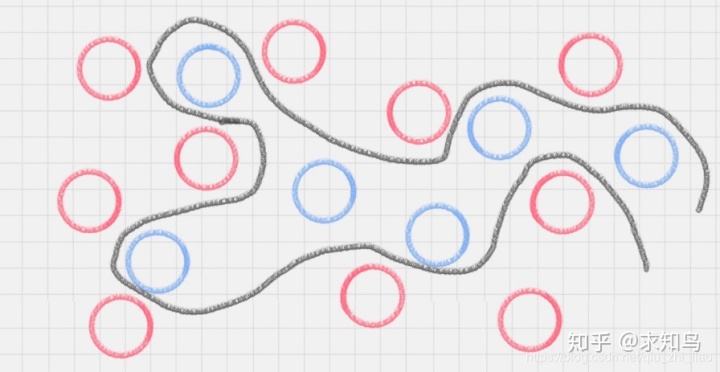
二维平面内，用曲线将颜色球分开了；进一步，三维立体层面？

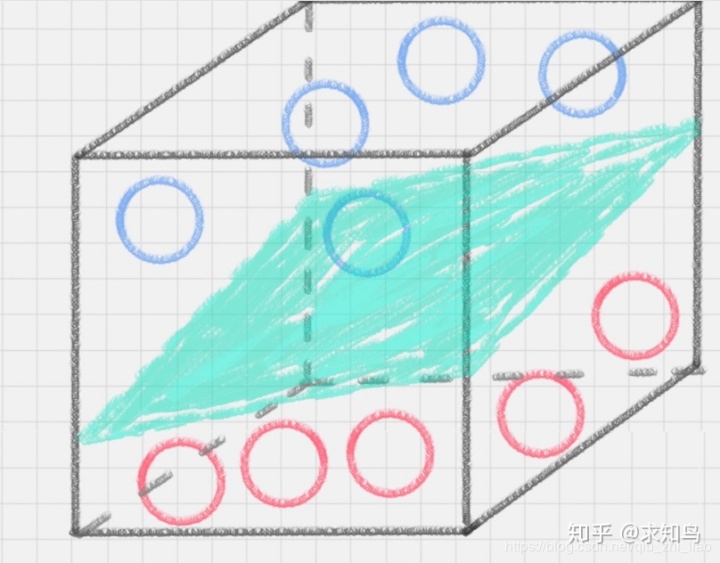
在这里，二维平面变成了三维空间。原来的曲线变成了一个平面。这个平面，就叫做超平面。

SVM 的工作原理

用 SVM 计算的过程就是帮我们找到那个超平面的过程，这个超平面就是我们的 SVM 分类器。

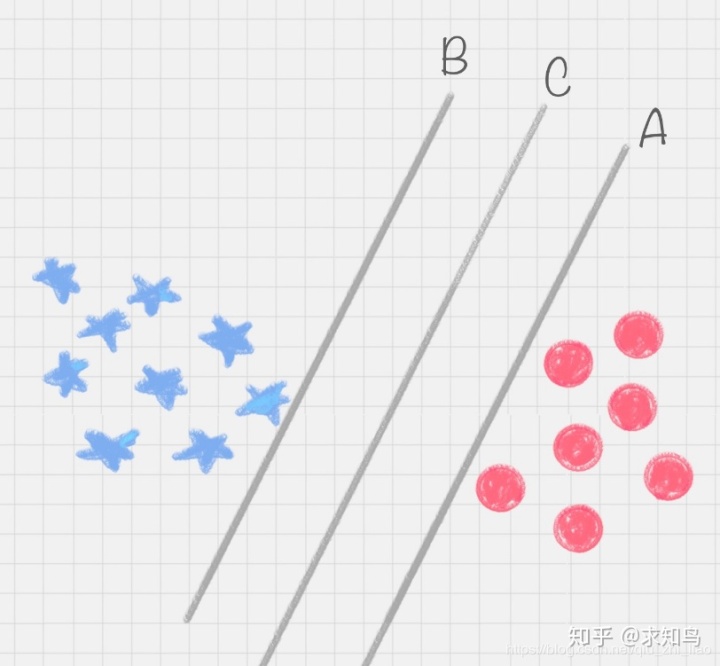
上图中，直线 A、直线 B 和直线 C，究竟哪种才是更好的划分呢？

B直线更好，因为B与蓝色球靠的很近；A直线更好，因为A与红色球更近；但，实际生活中，蓝色球可能会朝着红色区域移动，红色球会向着蓝色区域移动；所以，最终A直线更好，因为它的鲁棒性更好。

鲁棒性/抗变换性（英文：robustness）原是统计学中的一个专门术语，20世纪初在控制理论的研究中流行起来，用以表征控制系统对特性或参数扰动的不敏感性。

那怎样才能寻找到直线 C 这个更优的答案呢？这里，我们引入一个 SVM 特有的概念：分类间隔。

在保证决策面不变，且分类不产生错误的情况下，我们可以移动决策面 C，直到产生两个极限的位置：如图中的决策面 A 和决策面 B。极限的位置是指，如果越过了这个位置，就会产生分类错误。这样的话，两个极限位置 A 和 B 之间的分界线 C 就是最优决策面。极限位置到最优决策面 C 之间的距离，就是“分类间隔”，英文叫做 margin。

如果我们转动这个最优决策面，你会发现可能存在多个最优决策面，它们都能把数据集正确分开，这些最优决策面的分类间隔可能是不同的，而那个拥有“最大间隔”（max margin）的决策面就是 SVM 要找的最优解。

点到超平面的距离公式

必要的数学公式可以帮助我们理解模型的原理。

超平面的数学表达可以写成：

在这个公式里，w、x 是 n 维空间里的向量，其中 x 是函数变量；w 是法向量。法向量这里指的是垂直于平面的直线所表示的向量，它决定了超平面的方向。b是位移项，决定原点到超平面的距离。（法向量+距离可以唯一确定超平面的位置）

SVM 就是帮我们找到一个超平面，这个超平面能将不同的样本划分开，同时使得样本集中的点到这个分类超平面的最小距离（即分类间隔）最大化。

在这个过程中，支持向量就是离分类超平面最近的样本点，实际上如果确定了支持向量也就确定了这个超平面。所以支持向量决定了分类间隔到底是多少，而在最大间隔以外的样本点，其实对分类都没有意义。

所以说， SVM 就是求解最大分类间隔的过程，我们还需要对分类间隔的大小进行定义。

首先，我们定义某类样本集到超平面的距离是这个样本集合内的样本到超平面的最短距离。我们用 di 代表点 xi 到超平面 wxi+b=0 的欧氏距离。因此我们要求 di 的最小值，用它来代表这个样本到超平面的最短距离。di 可以用公式计算得出：

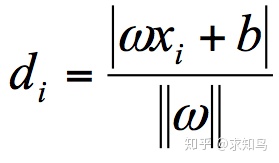
其中||w||为超平面的范数，di 的公式可以用解析几何知识进行推导；我们寻找的最大间隔

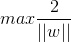
就是支持向量机。

支持向量机的求解通常借助于凸优化技术，如何提高效率，使得svm能够运用到大规模数据中，一直是研究的热点问题。

最大间隔的优化模型

在数学上，最大间隔的优化模型是一个凸优化问题（凸优化就是关于求凸集中的凸函数最小化的问题）。通过凸优化问题，最后可以求出最优的 w 和 b，也就是我们想要找的最优超平面。中间求解的过程会用到拉格朗日乘子，和 KKT（Karush-Kuhn-Tucker）条件。

硬间隔、软间隔和非线性 SVM

假如数据是完全的线性可分的，那么学习到的模型可以称为硬间隔支持向量机。换个说法，硬间隔指的就是完全分类准确，不能存在分类错误的情况。软间隔，就是允许一定量的样本分类错误。

我们知道，实际工作中的数据没有那么“干净”，或多或少都会存在一些噪点。所以线性可分是个理想情况，这时，我们需要使用到软间隔 SVM（近似线性可分），比如下面这种情况：

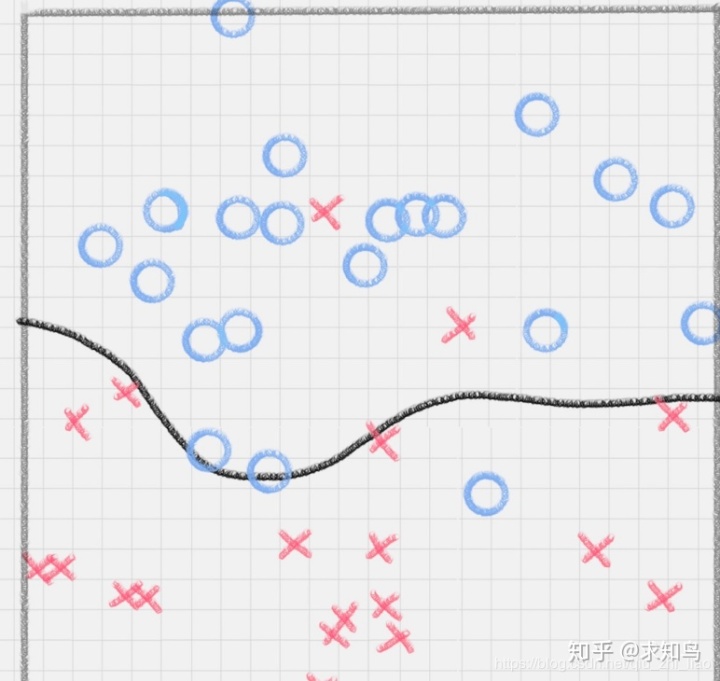
另外还存在一种情况，就是非线性支持向量机。

下图中的两类数据，分别分布为两个圆圈的形状。那么这种情况下，不论是多高级的分类器，只要映射函数是线性的，就没法处理，SVM 也处理不了。

这时，我们需要引入一个新的概念：核函数。它可以将样本从原始空间映射到一个更高维的特质空间中，使得样本在新的空间中线性可分。

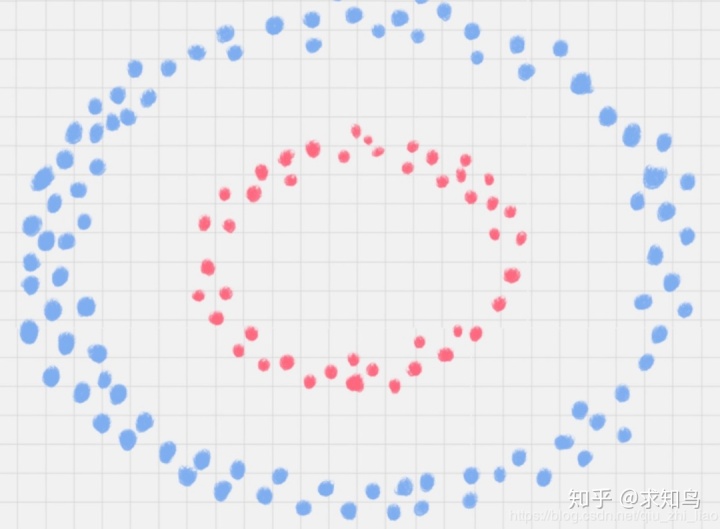
所以在非线性 SVM 中，核函数的选择就是影响 SVM 最大的变量。最常用的核函数有线性核、多项式核、高斯核、拉普拉斯核、sigmoid 核，或者是这些核函数的组合。这些函数的区别在于映射方式的不同。通过这些核函数，我们就可以把样本空间投射到新的高维空间中。新的高纬度空间，就可以使用之前的推导公式下进行推导。