excel求回归直线方程的公式_高中数学：线性回归方程

线性回归是利用数理统计中的回归分析来确定两种或两种以上变数间相互依赖的定量关系的一种统计分析方法，是变量间的相关关系中最重要的一部分，主要考查概率与统计知识，考察学生的阅读能力、数据处理能力及运算能力，题目难度中等，应用广泛．

一 线性回归方程公式

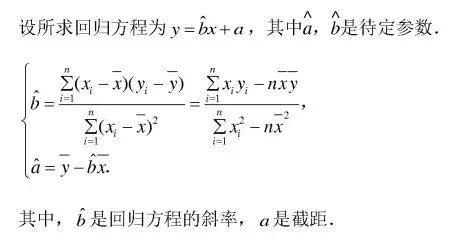
二 规律总结

(3)回归分析是处理变量相关关系的一种数学方法．主要用来解决：

①确定特定量之间是否有相关关系，如果有就找出它们之间贴近的数学表达式；

②根据一组观察值，预测变量的取值及判断变量取值的变化趋势；

③求线性回归方程．

三 线性回归方程的求法

例1

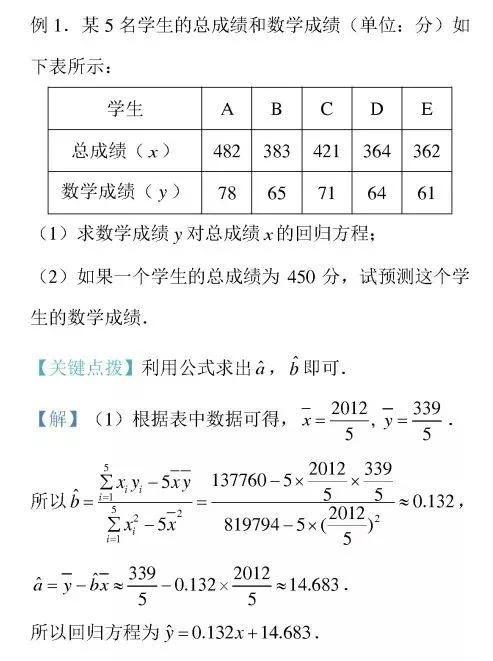
四 线性回归方程的应用

例2

例3

例4

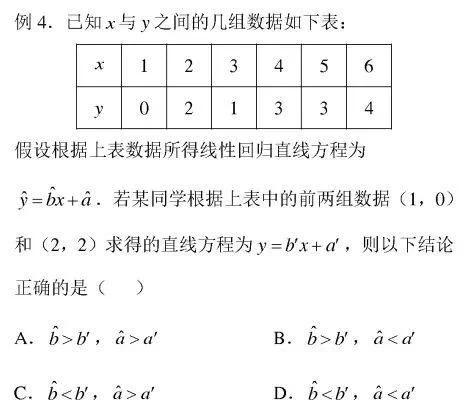
例5

例6

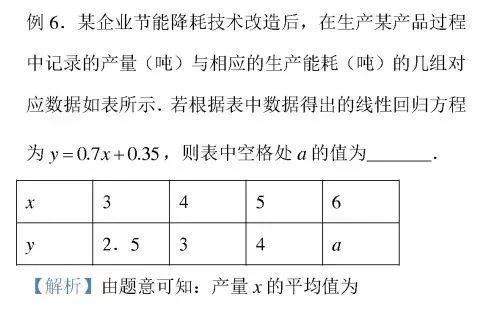
推导2个样本点的线性回归方程

例7 设有两个点A(x1，y1)，B(x2，y2)，用最小二乘法推导其线性回归方程并进行分析。

解：由最小二乘法，设，则样本点到该直线的“距离之和”为

从而可知：当时，b有最小值。将代入“距离和”计算式中，视其为关于b的二次函数，再用配方法，可知：

此时直线方程为：

设AB中点为M，则上述线性回归方程为

可以看出，由两个样本点推导的线性回归方程即为过这两点的直线方程。这和我们的认识是一致的：对两个样本点，最好的拟合直线就是过这两点的直线。

上面我们是用最小二乘法对有两个样本点的线性回归直线方程进行了直接推导，主要是分别对关于a和b的二次函数进行研究，由配方法求其最值及所需条件。实际上，由线性回归系数计算公式：

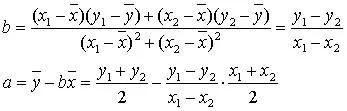
可得到线性回归方程为

设AB中点为M，则上述线性回归方程为

。

求回归直线方程

例8 在硝酸钠的溶解试验中，测得在不同温度下，溶解于100份水中的硝酸钠份数的数据如下

描出散点图并求其回归直线方程.

解：建立坐标系，绘出散点图如下：

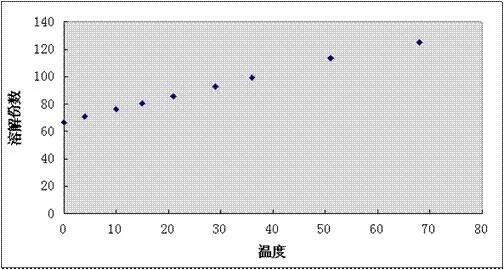
由散点图可以看出：两组数据呈线性相关性。设回归直线方程为：

由回归系数计算公式：

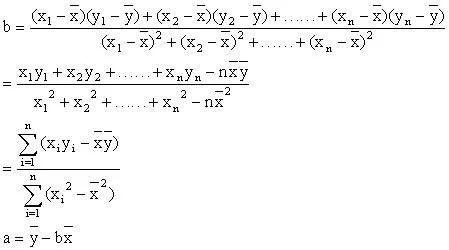
可求得：b=0.87，a=67.52，从而回归直线方程为：y=0.87x+67.52。

三、综合应用

例3、假设关于某设备的使用年限x和所支出的维修费用y(万元)有如下统计资料：

(1)求回归直线方程；(2)估计使用10年时，维修费用约是多少？

解：(1)设回归直线方程为：

(2)将x = 10代入回归直线方程可得y = 12.38，即使用10年时的维修费用大约是12.38万元。

线性回归方程也是高考常考考点之一，希望同学们能认真学习，掌握线性回归方程的求法及应用，认真体会线性回归方程的求解过程，理解变量间的相关关系，从而体会统计思想在实际生活中的应用及重要．

▍ 来源：综合网络

▍ 编辑：Wordwuli

▍ 声明：如有侵权，请联系删除；若需转载，请注明出处。

【来源：点知教育】

声明：转载此文是出于传递更多信息之目的。若有来源标注错误或侵犯了您的合法权益，请作者持权属证明与本网联系，我们将及时更正、删除，谢谢。