linux多线程编程实现圆周率,linux环境下使用Monte Carlo计算π

1 实验题目

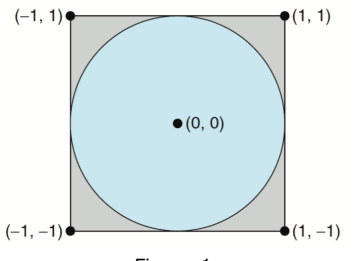
计算π的一个有趣方法是使用一个称为Monte Carlo的技术，这种技术涉及随机。该技术工作如下：假设有一个圆，它内嵌一个正方形，如下图所示。

首先，通过(x,y)坐标生成一系列的随机点。这些点应在正方形内。在这些随机产生的点中，有的会落在圆内。接着，根据下面公式，估算π。

π= 4✖️(圆内的点数)/(总点数)

(1)请编写一个多线程版的算法，它创建一组子线程，每个子线程产生一组随机点，并确定点是否落在圆内。每个子线程更新所有落在园内的点的全局计数。当所有子线程计算完毕后，使用父线程计算π。(通过采用互斥锁，保护对共享全局变量的更新)？

(2)针对题目(1)请考虑一下，该怎样来提高计算π的性能(速度)？请实现相关的思想或算法的代码，并给出分析说明和实验数据证明！

2蒙特卡洛方法介绍

百度百科：百度百科

蒙特卡洛法，也称为统计模拟方法，是二十世纪四十年代中期由于科学技术的发展和电子计算机的发明，而被提出的一种以概率统计理论为指导的一类非常重要的数值计算方法。是指使用随机数(或更常见的伪随机数)来解决很多计算问题的方法。

3分析思路

①蒙特卡洛的本质是统计方法，所以必然要获取大量的数据才能得到较为精确的圆周率，

②在计算π的公式中，S=πrr，所以π=S/(rr)，当r=1时，π此时等于S

③可以假设圆的半径为1，并且此时圆的外接正方形为22=4，设圆心位于坐标轴(0，0)④通过产生大量位[-1,1]的随机数坐标(x,y),即-1<=x<=1,-1<=y<=1,若x^2+y^2<=1,则某个随机点落在圆内，否则落在圆外

⑤最终我们所求的圆周率π即为随机数的个数和/落在园内的随机数和。

⑥通过使用互斥锁来保证结果的正确性

4代码实现

4.1 安装插件

POSIX下开发多线程主要依赖的就是Pthread。使用它需要包含头文件#include。因为这个库在Pthread之中，在编译的时候需要加上参数：-lpthread.

4.1.1

在终端输入命令

sudo apt-get install glibc-doc

然后输入密码