lasso回归_【机器学习-回归】岭回归与Lasso回归

书接上文。

不愿露名的笨马：【机器学习-回归】梯度下降(SGD/BGD/MBGD)​zhuanlan.zhihu.com

这一节我们主要考虑矩阵形式。考虑BGD的情形。

BGD情形下，全体样本损失函数：

进一步，有：

为求其最小值，应有偏导数为0：

化简，即有：

注：不会矩阵求导的萌新可以点开这个链接：

https://blog.youkuaiyun.com/daaikuaichuan/article/details/80620518​blog.youkuaiyun.com

到这里我们发现，模型的目标参数是对样本有一定要求的，即

的行列式值不宜为0，即

特征之间不宜存在共线性关系。而实际数据当中，自变量之间可能存在高度自相关性，一方面可以通过业务知识删除共线性关系；另一方面，可以通过 岭回归(Ridge Regression)/Lasso回归(Lasso Regression)来避免这个问题。

岭回归

岭回归的思路也比较简单，就是增加了个扰动项：

可以看到，偏回归系数

值在岭回归过程中通过干扰系数

变动，当

时，岭回归即退化成普通线性回归模型的系数值。

而其本质上，则是求解这个最优化问题：

注意到右侧添加了一个L2范数惩罚项。L2范数使得

的各分量不会过大(防止模型过拟合、降低模型复杂度)，起到一个收缩作用；而收缩的力度则通过

平衡。见下图：

L2惩罚项下模型复杂度、方差、偏差之间权衡，侵删

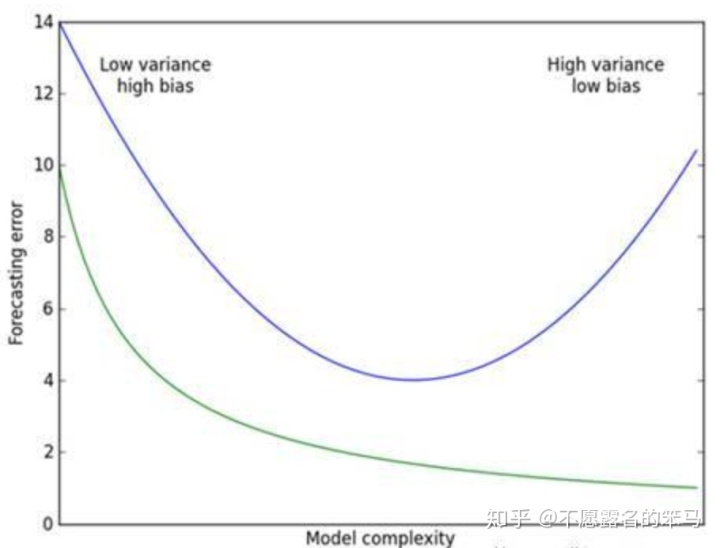
我们知道，预测误差=偏差(bias)+方差(variance)+噪声样本干扰(这一部分难以优化)。因此如何权衡方差与偏差之间的关系就显得很重要。在该图中，

较小时(左侧)为欠拟合，

较大时(右侧)为过拟合。因此

平衡误差与方差之间的关系显得较为重要，可以通过调整该参数以获取较为理想的岭回归系数。

岭回归的几何解释

说一千道一万，只说惩罚项添加以及它的好处还是不太能直观了解它到底在解空间是如何优化的，因此结合几何解释服用更佳。

将上述最优化问题拆分为以下两个条件：

损失函数：

约束条件：

为什么要添加这个约束条件？我们需要明确岭回归的目的，就是为了解决线性回归中的特征共线性的问题。由于特征之间共线性关系的存在，对应的几个特征之间的系数存在抵消关系，可以变得特别大。因此，增加一个平方和的约束，使得各特征的系数都被压制在一个范围内，降低模型的复杂度。

对应到几何图形中，如图(这里选取了特征数为2来展示)：

损失函数对应半椭球体，约束条件对应圆柱体

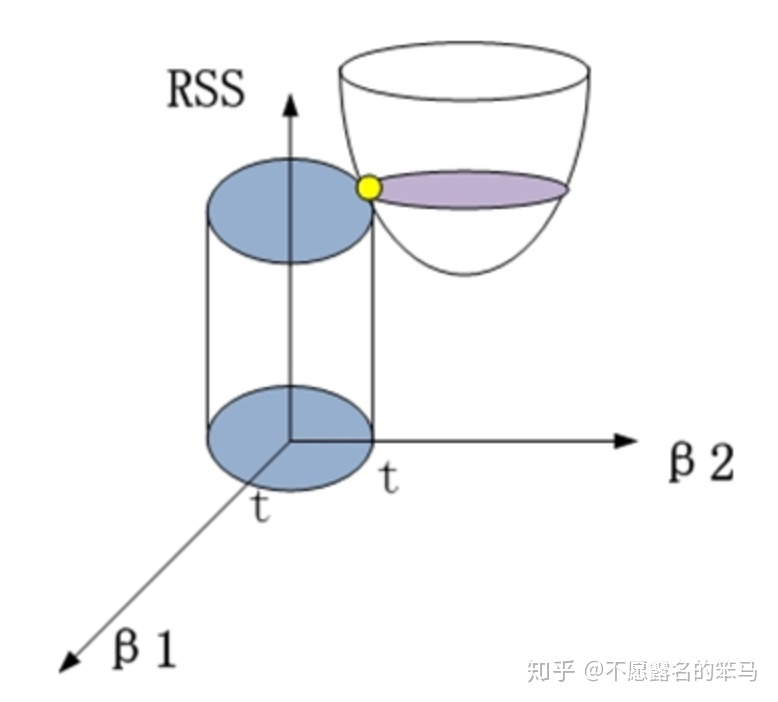
则岭回归所求解即为二者的交集，即黄点。

投影到平面上则更加直观：

平面上的岭回归几何解释

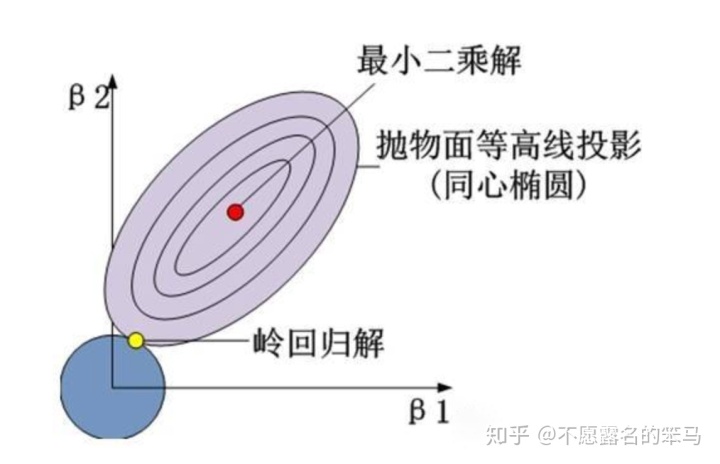
所求解即为圆与同心椭圆的切点。

下面附上几条性质：

1. 岭回归系数是最小二乘法估计的线性变换；
2. 岭回归系数是有偏的；
3. 时，岭回归系数具有压缩性(参数模降低);
4. 存在
   使得岭回归优于线性回归。

LASSO回归

LASSO回归设计的出发点与岭回归类似，都是为了解决特征之间存在共线性时线性回归的问题。区别在于，岭回归采用的是L2范数惩罚项，而LASSO回归采用的则是L1范数惩罚项，即最优化问题变为：

同理，可以转化为如下两个条件：

损失函数：

约束条件：

对应平面图则为：

平面上LASSO回归的几何解释

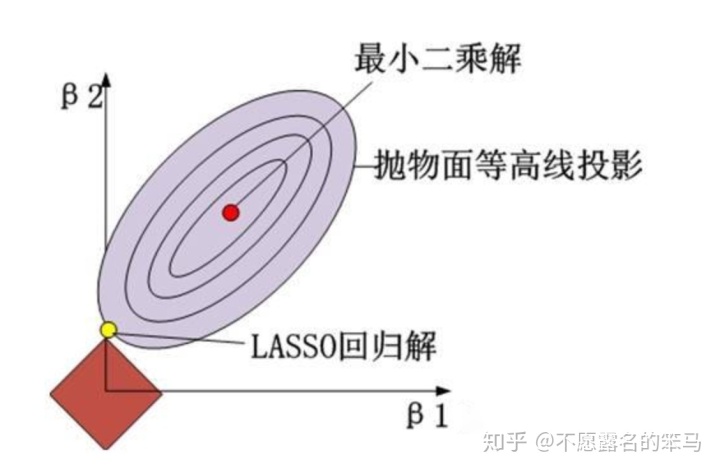
由于是L1范数，因此会出现"棱角"。当"棱角"与抛物面相交时，就会导致特征项易出现0(正方形在这里斜率为±1，不像圆相切要求较为苛刻)，因而相较于L2范数通过降低各系数的绝对值而防止过拟合、降低模型复杂度而言，L1范数惩罚项易构造稀疏矩阵，有特征选择作用，同时也有一定程度防止过拟合的作用。

回到第一篇文章的图，到这里应该也就理解了为什么，样本数多时候使用SGD、特征选择用Lasso、非特征选择用岭回归了。(注：ElasticNet属于Lasso与Ridge的过渡选择，这里不详细介绍了)

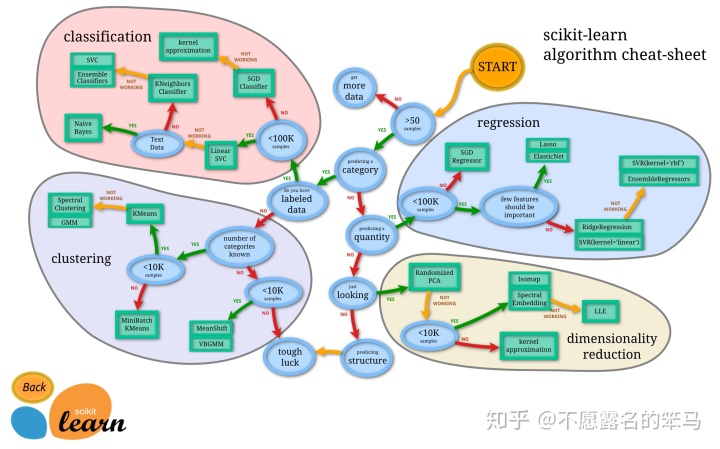
sklearn包中的岭回归与Lasso回归的应用

from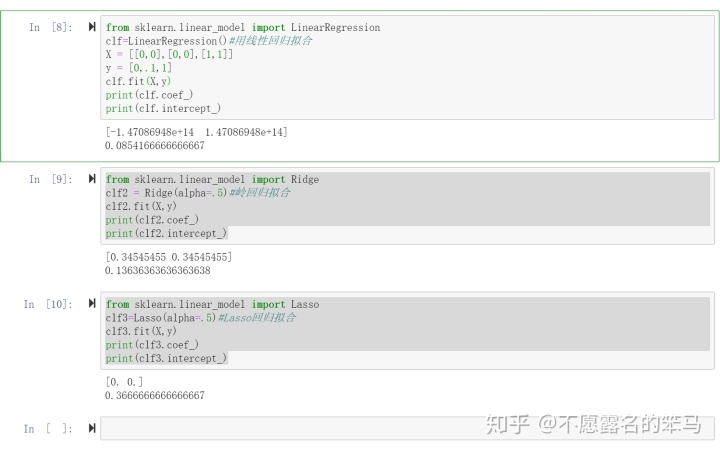 

可以看出，线性回归在不满足前提条件时，解出的答案已不具备可信度，Ridge与Lasso则可以给出一个可以接受的答案

到这里，线性回归的相关历程、损失函数、优化方法、几何解释已经阐述完毕，不了解的小伙伴可以反复观看这几节。下一节将讲述逻辑回归。

不愿露名的笨马：【机器学习-回归】线性回归​zhuanlan.zhihu.com

不愿露名的笨马：【机器学习-回归】梯度下降(SGD/BGD/MBGD)​zhuanlan.zhihu.com