施密特正交化计算器_如何理解施密特（Schmidt）正交化

https://www.zhihu.com/video/1238056375189774336

为什么要使用施密特正交化法

• 在一个平面，或者三维空间中，任意一点都可以被坐标系表示出来。而我们更喜欢的是单位直角坐标系，因为在一个单位直角坐标系中，任意一个向量的坐标分量，通过简单的投影就可以搞定。

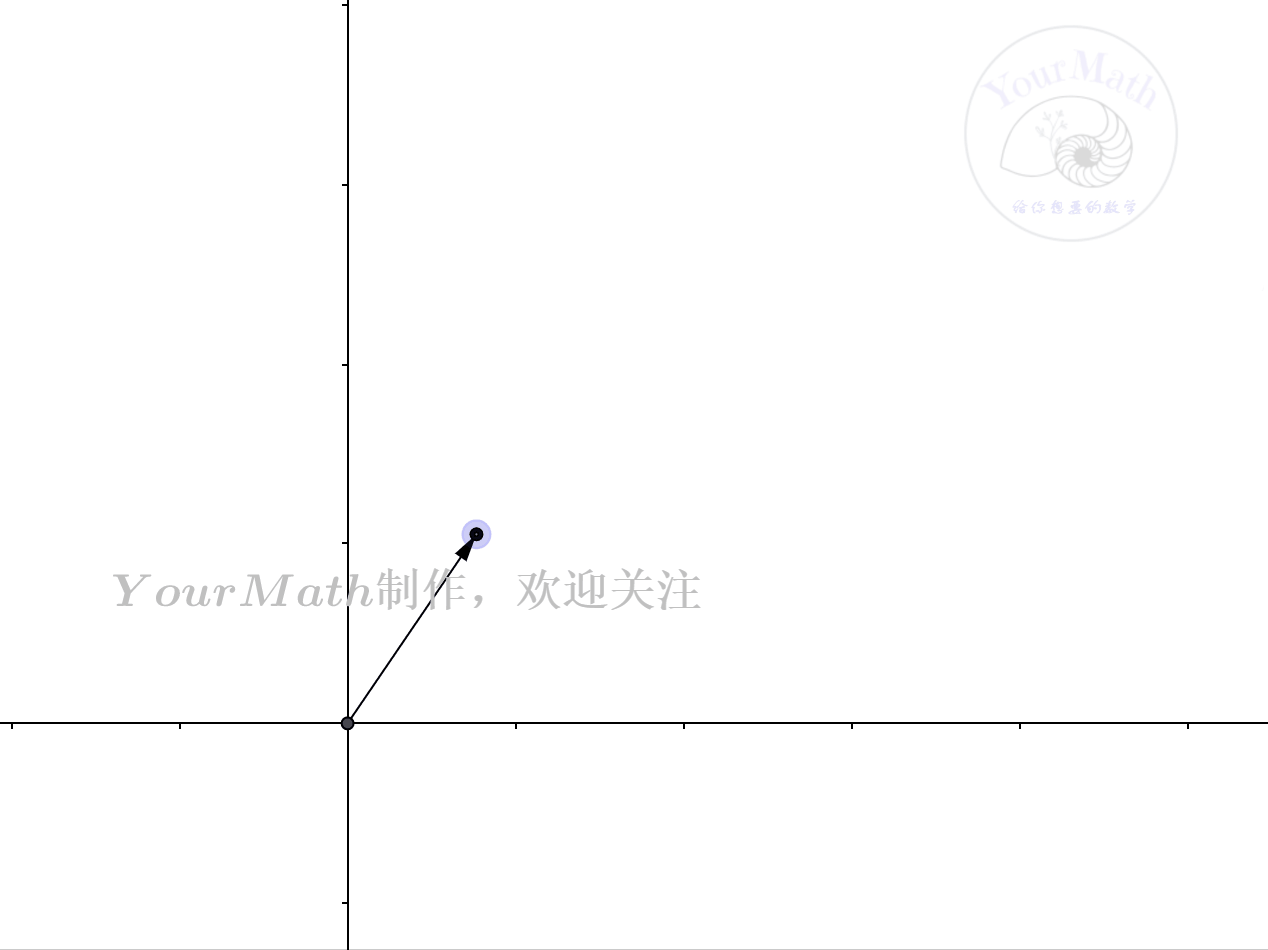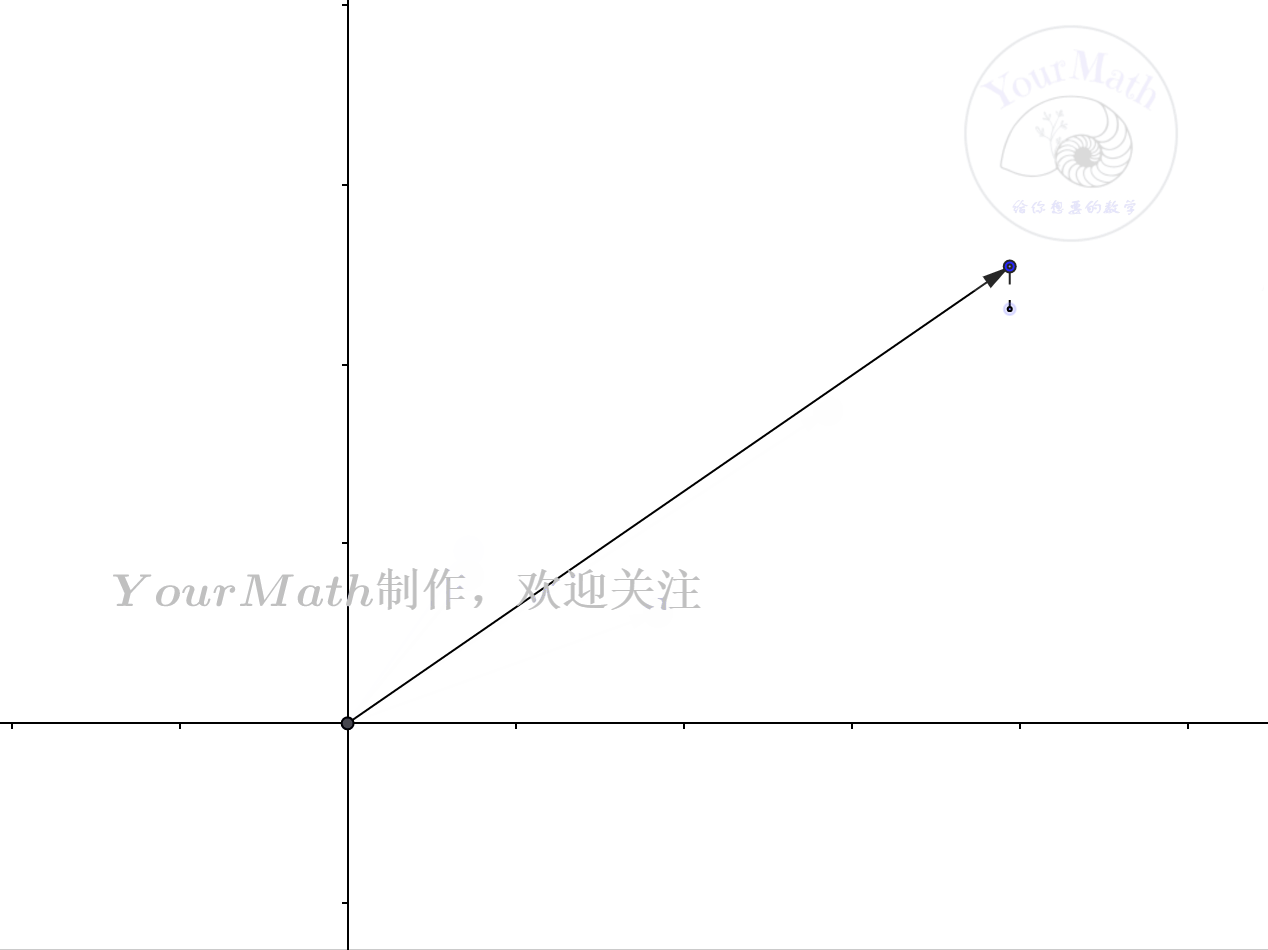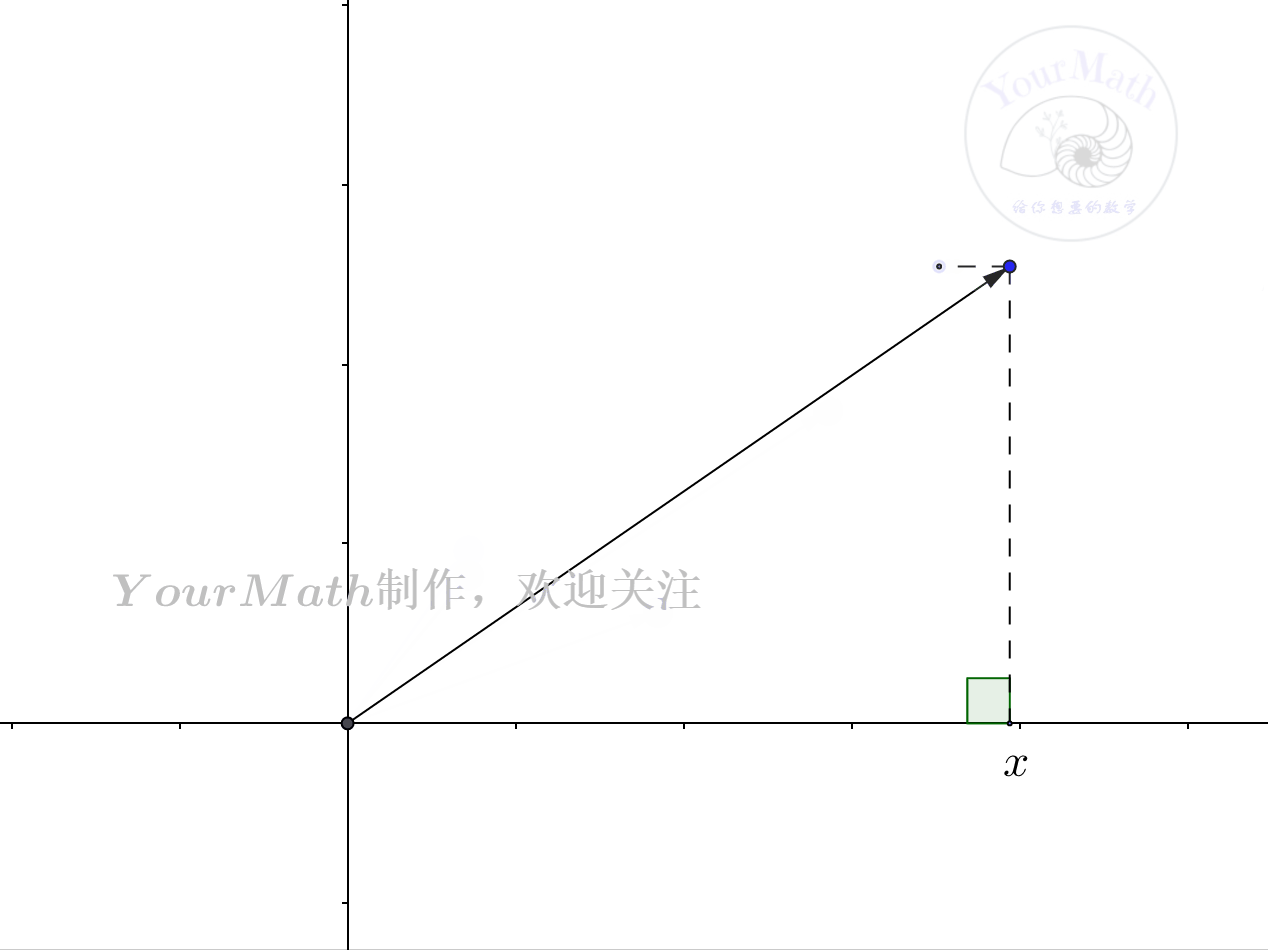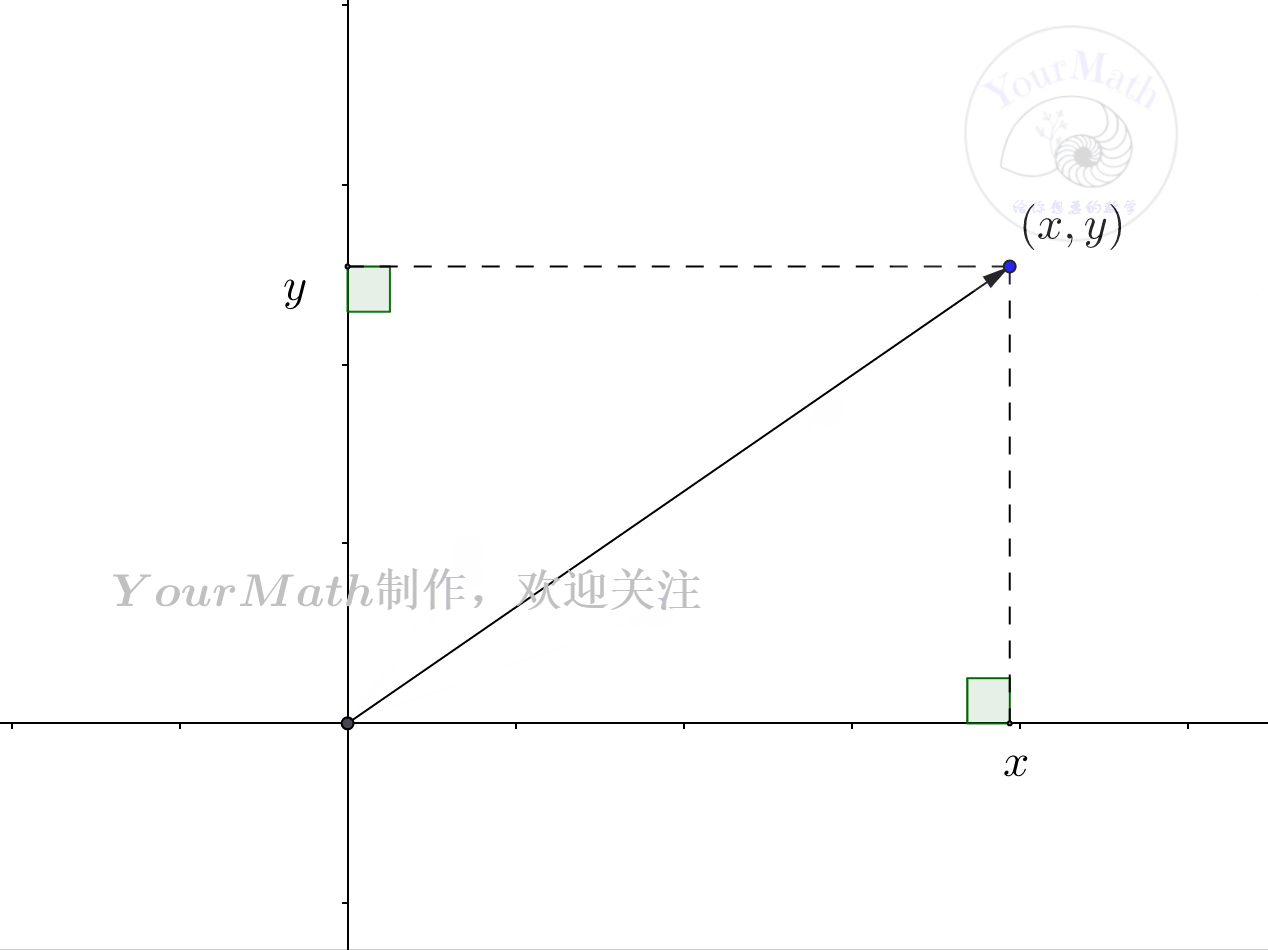
• 因此，如何找到欧式空间的一个“直角坐标系”，变得非常重要。施密特正交化法就告诉我们了一种把“任意坐标系”变为“直角坐标系”的方法。

---

如何理解欧氏空间

中的施密特正交化法

• 我们首先需要理解一个向量
  在另外一个向量
  的投影公式。只要利用正交的定义，就很容易知道
  在
  的投影向量为

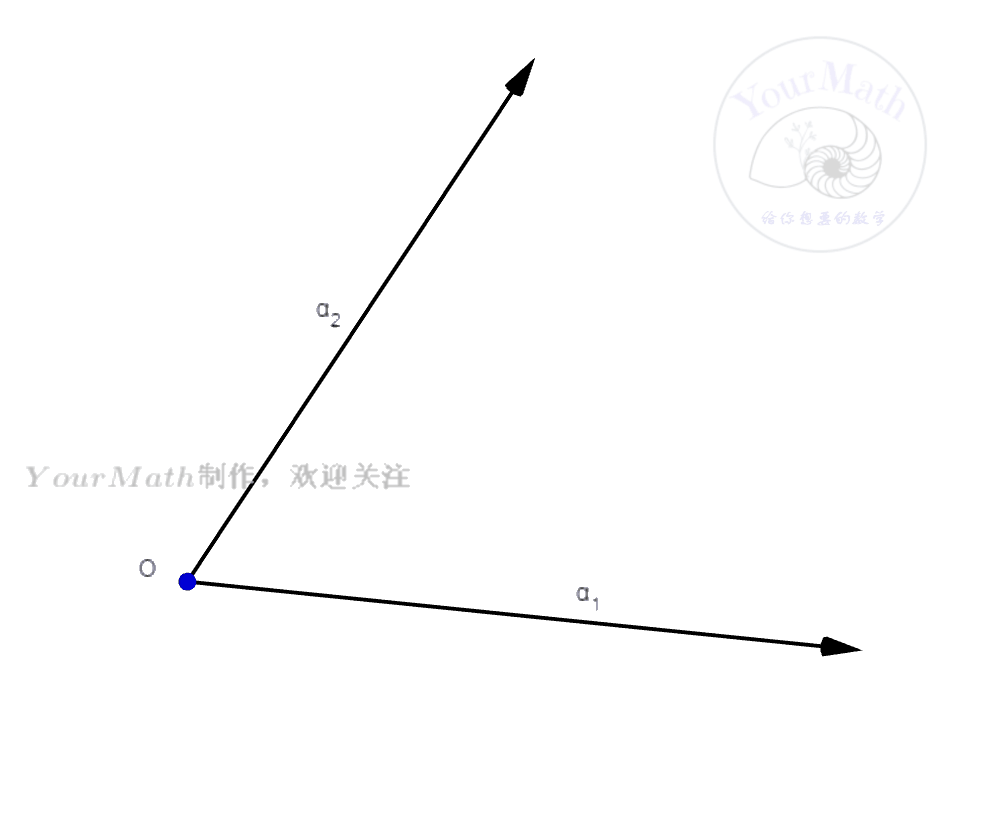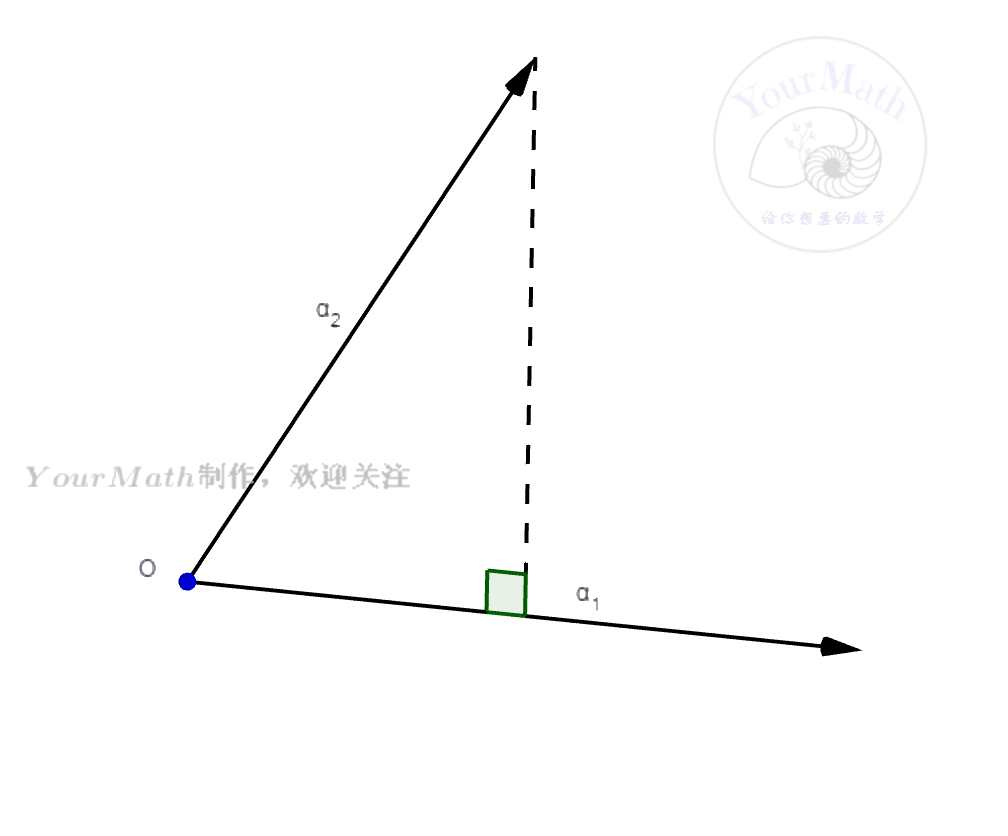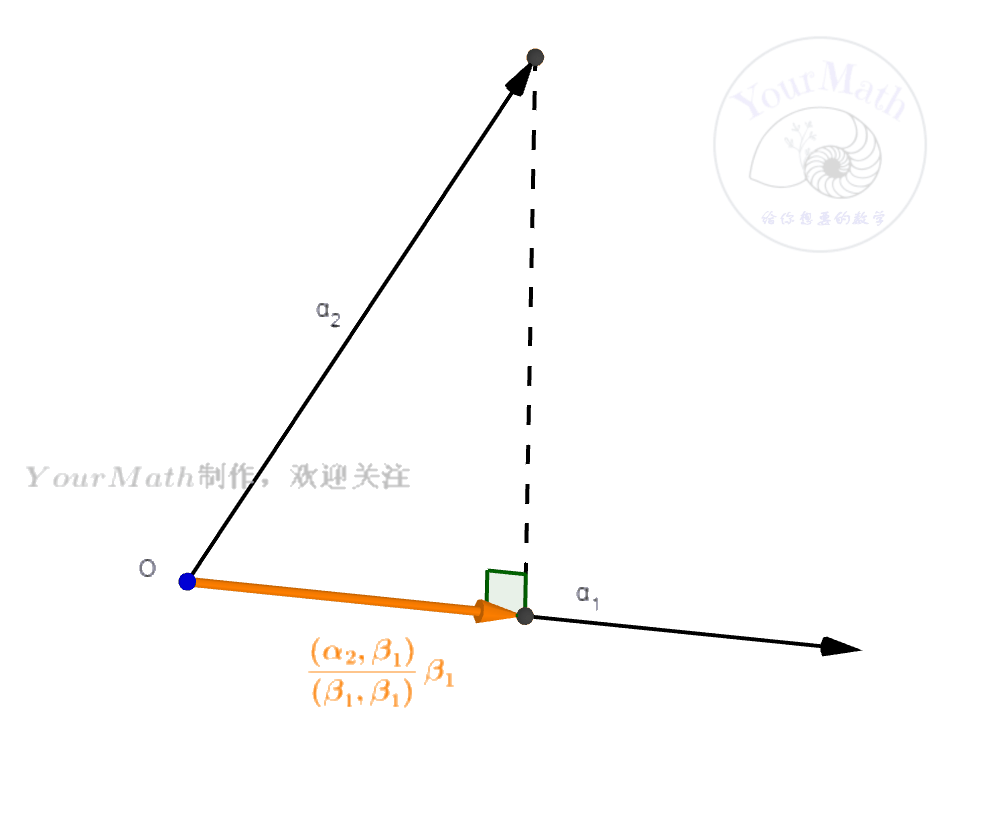
利用这个投影公式，我们便可以轻松理解施密特正交化法。

二维平面空间的情况

• 平面上任意两个不共线的向量都可以构成平面的一个坐标系(也就是一组基)，我们可以利用这两个向量之间的投影得到两个正交的向量：
  • Step1：令
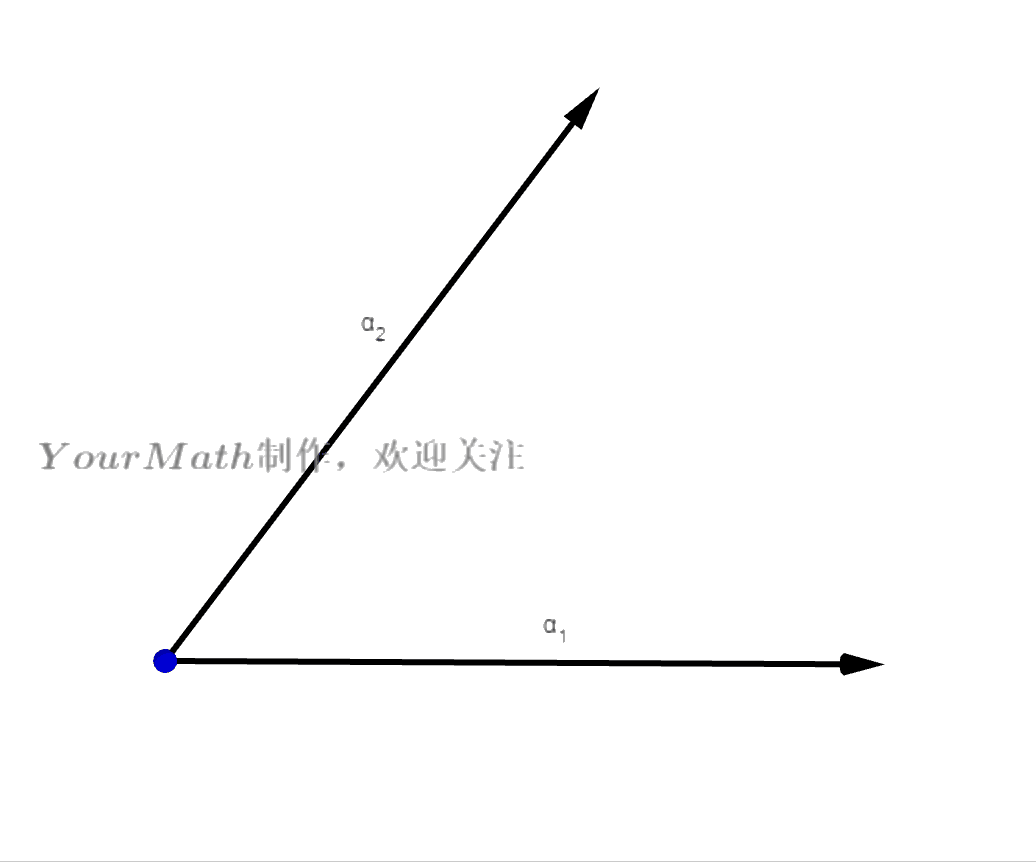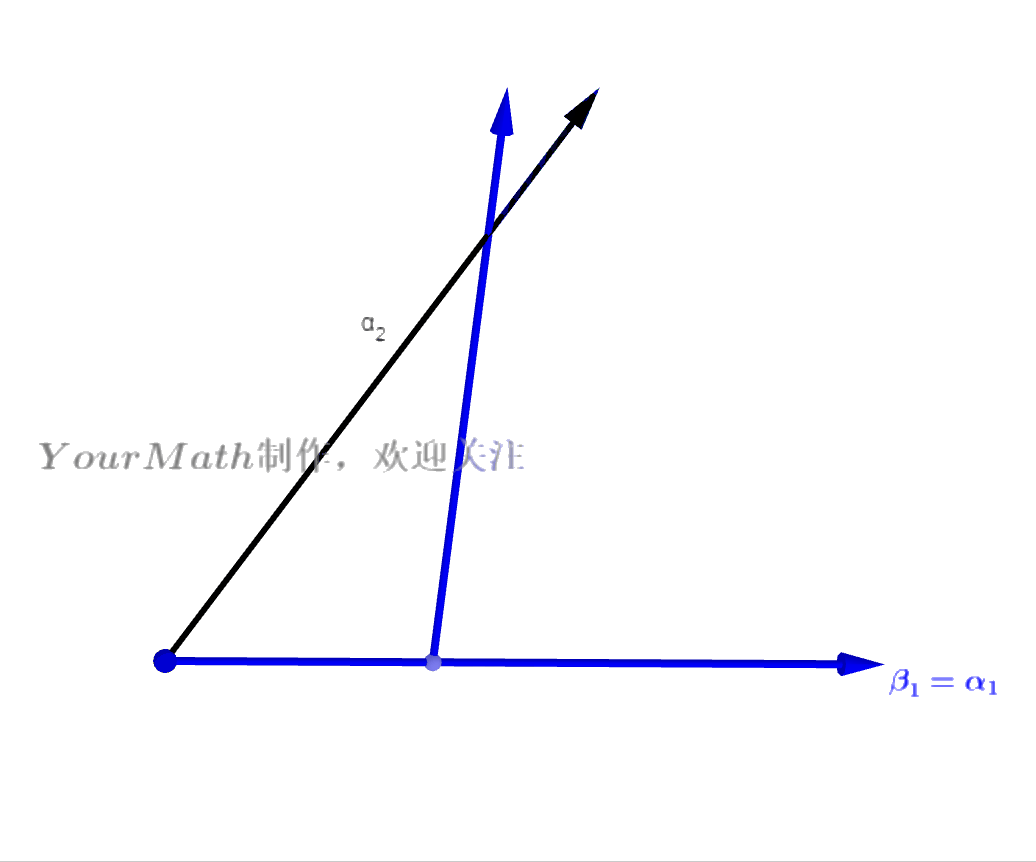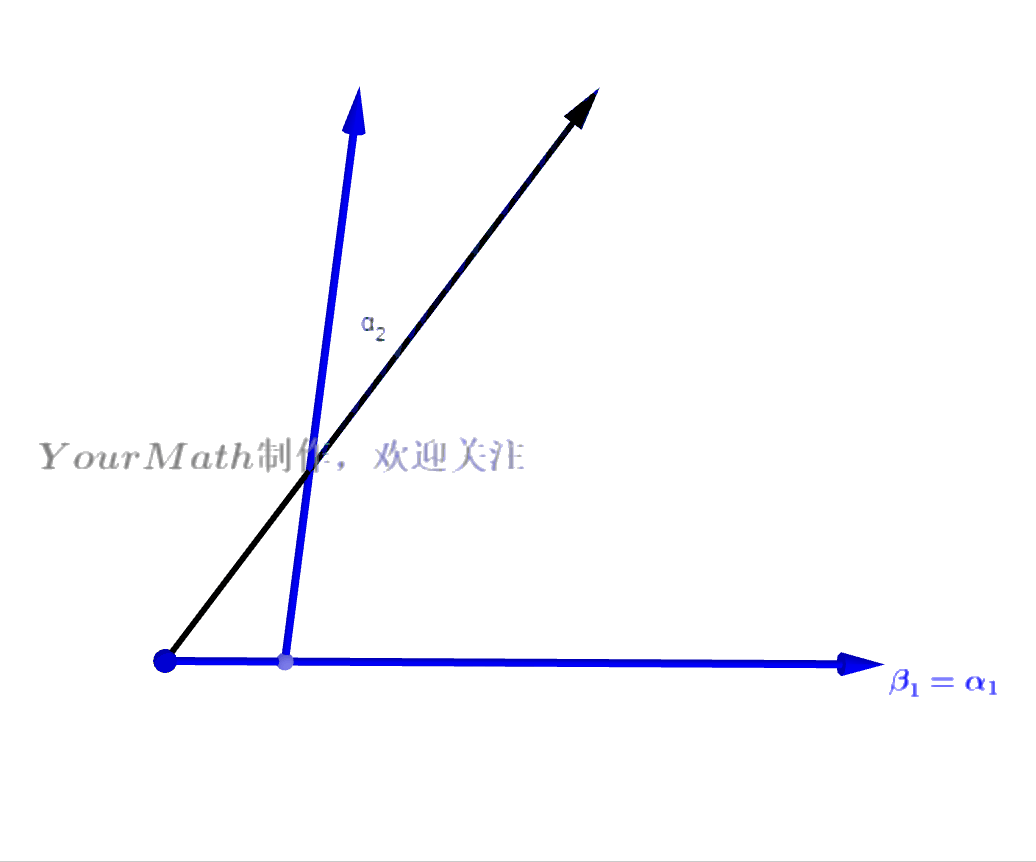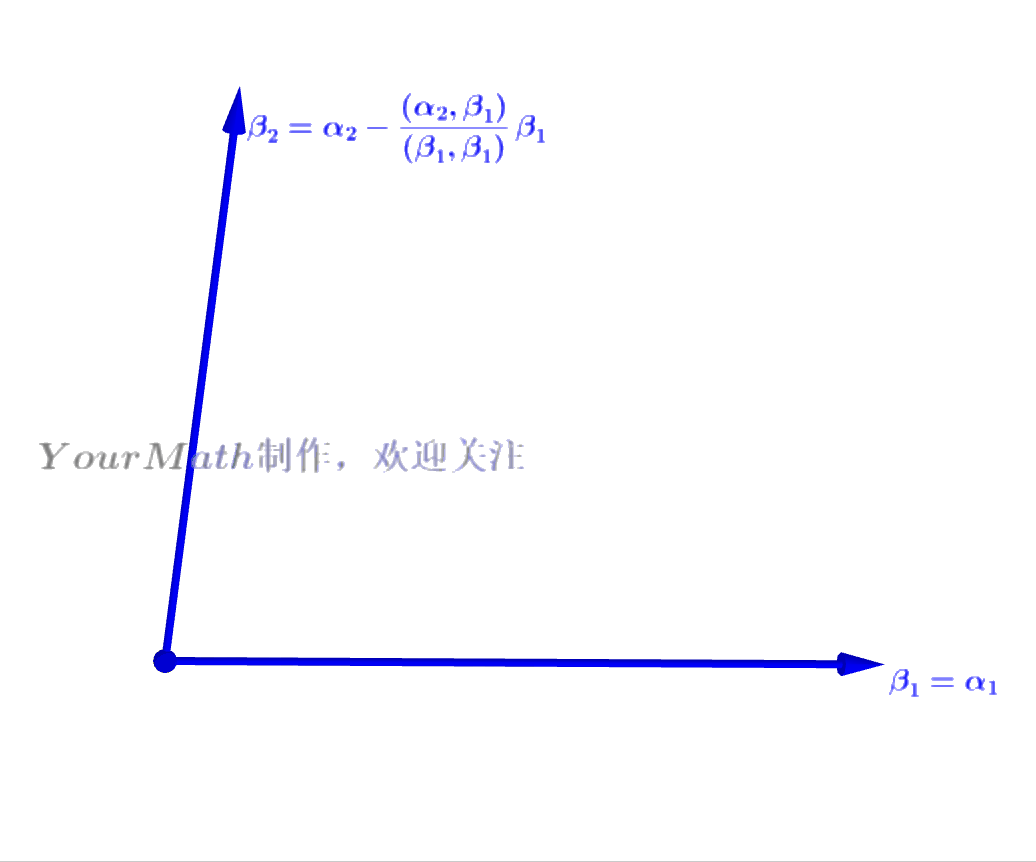
  • Step2: 做向量
    在向量
    的投影，并与
    做差得到

三维立体空间的情况

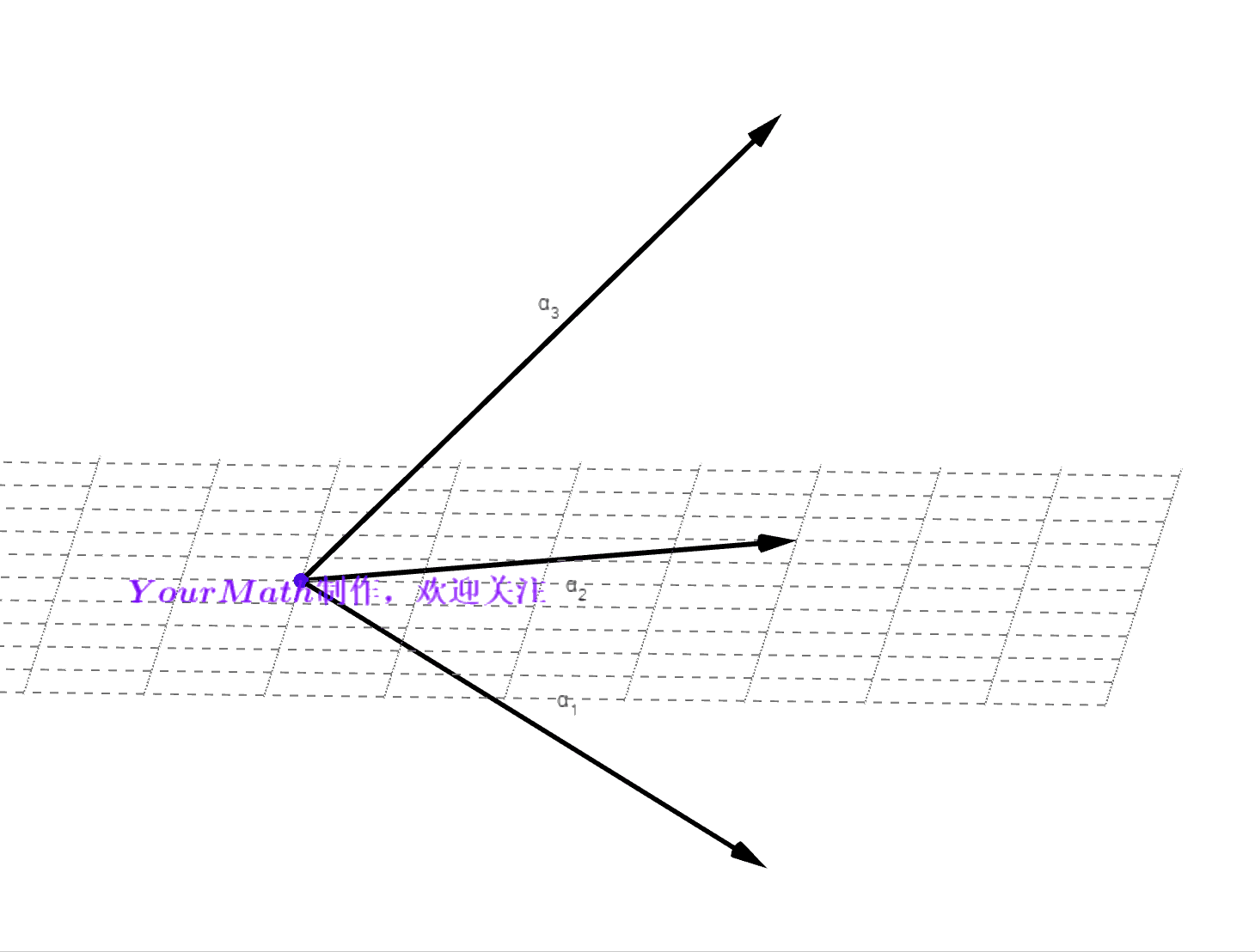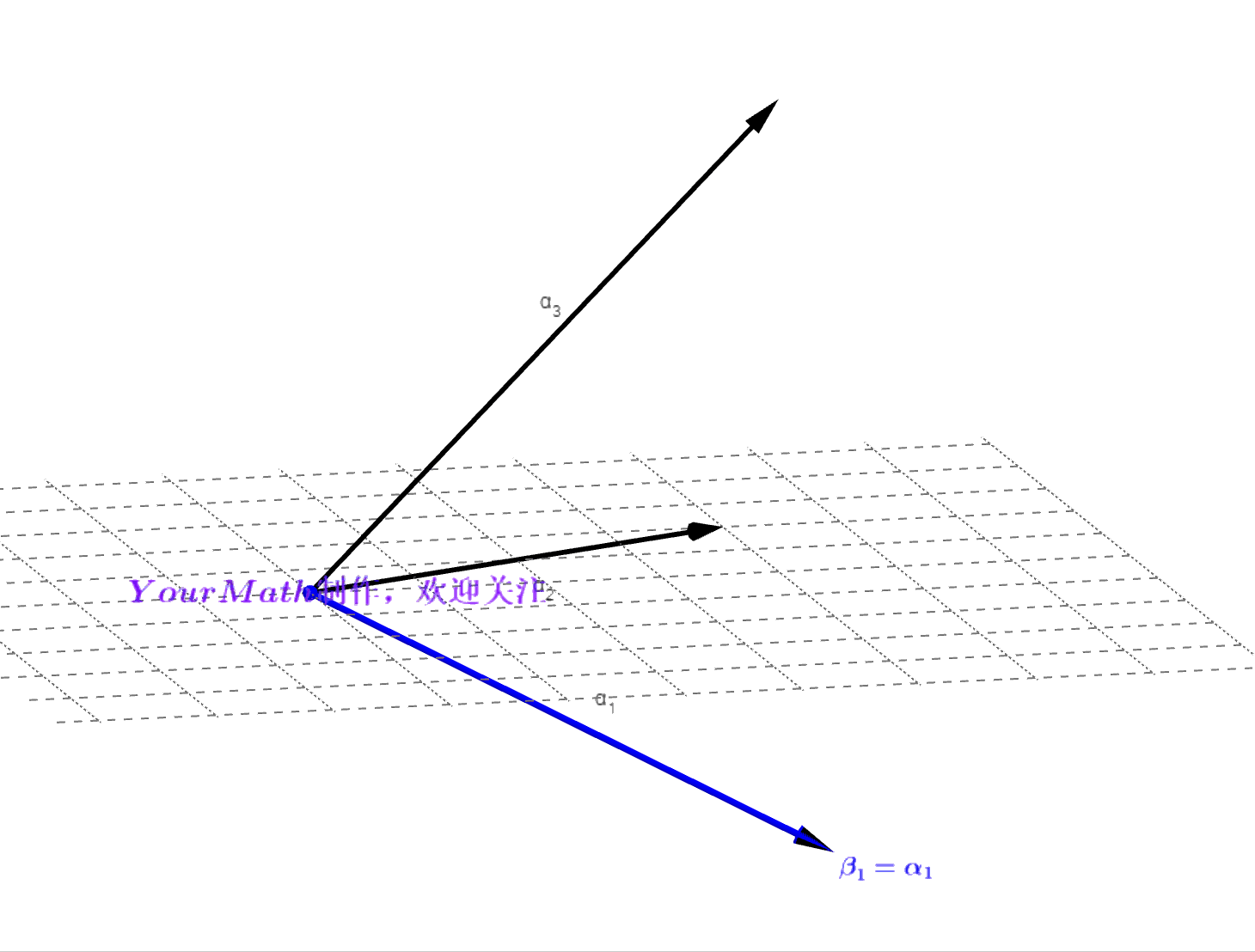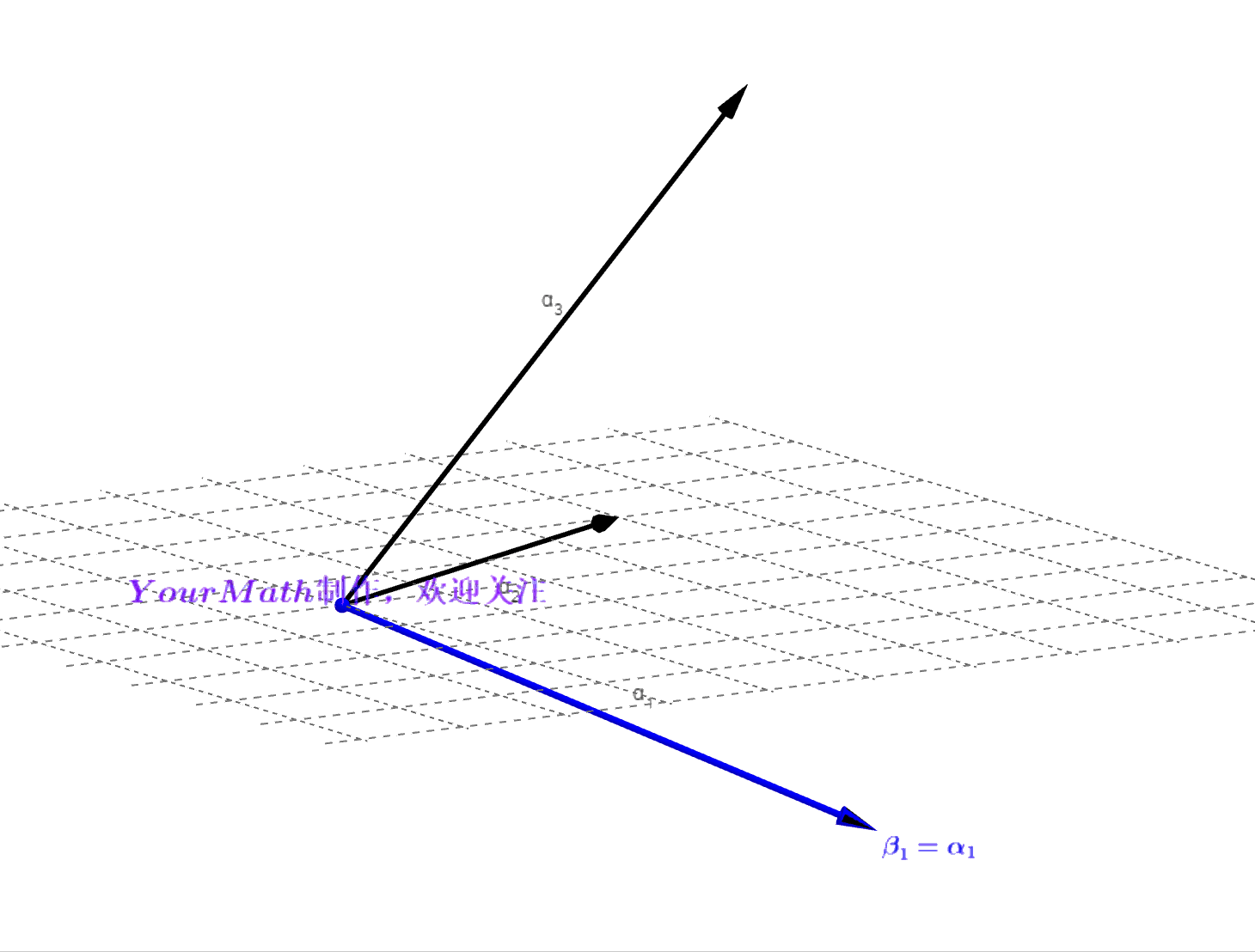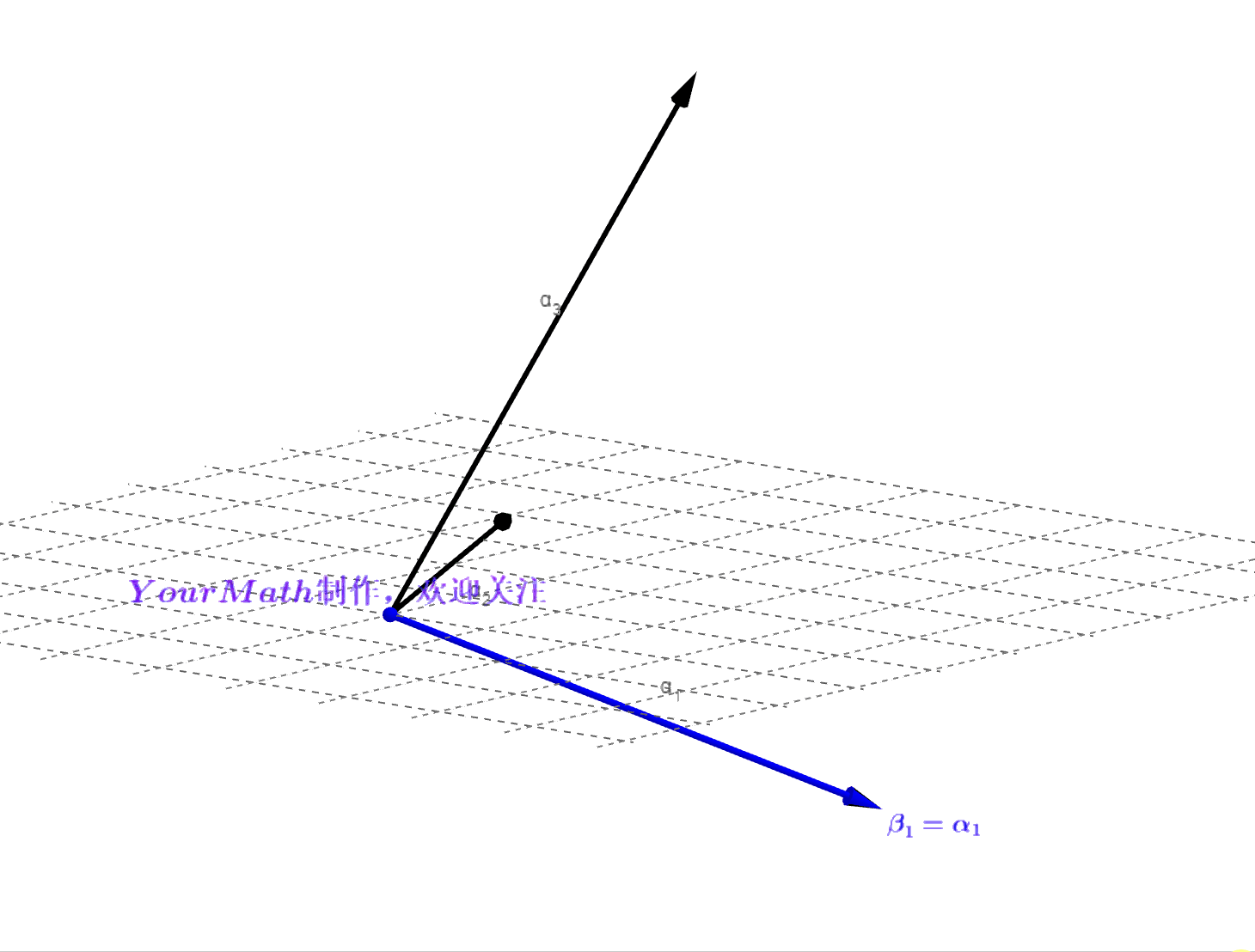
• 对于一个三维欧氏空间来说，首先可以轻松找到一组基：
  • Step1：任意取一个非零向量
  • Step2: 除去非零向量
    所在的直线后，任意取一个非零向量
  • Step3: 除去非零向量
    所在的平面，任意取一个非零向量
    。

图。。。。。

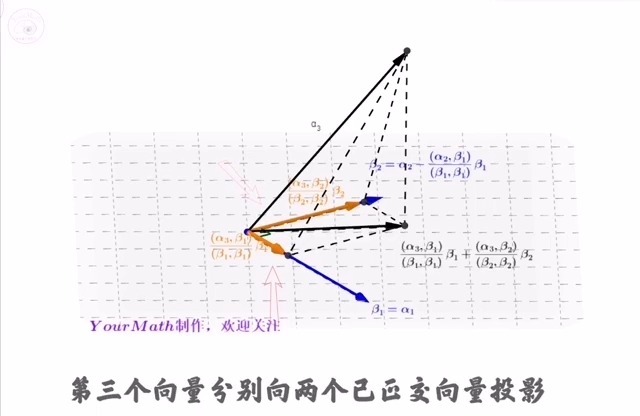
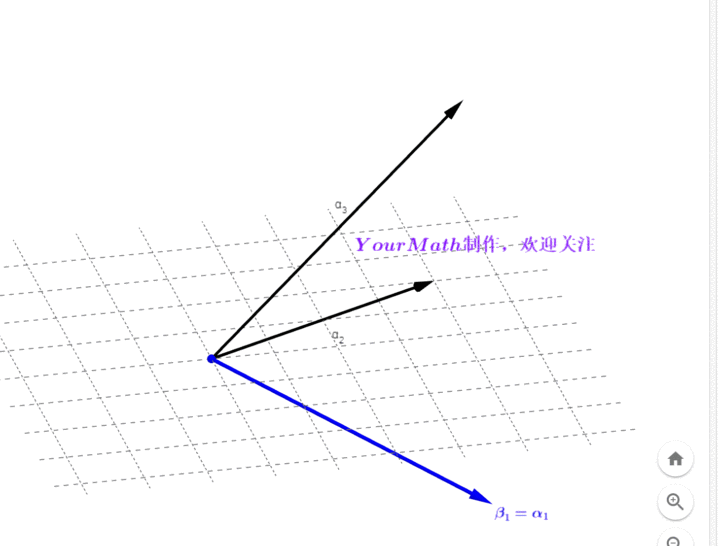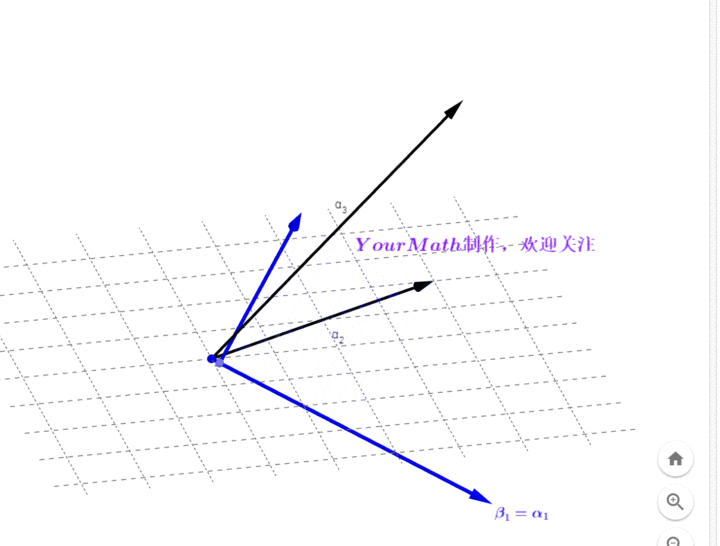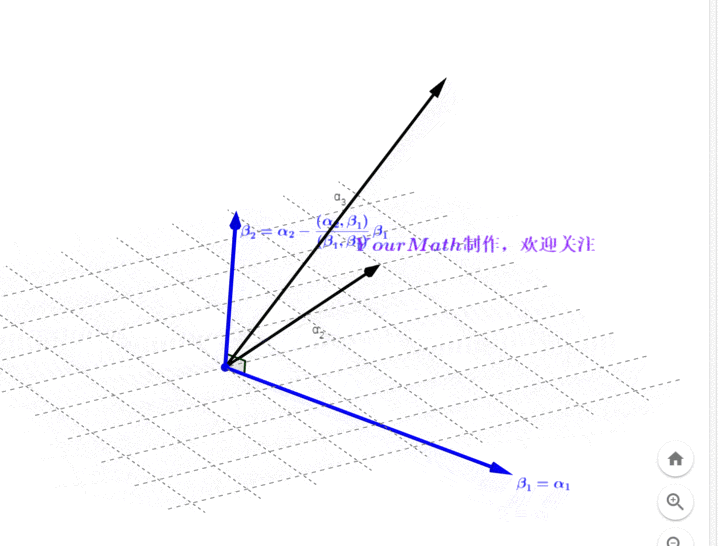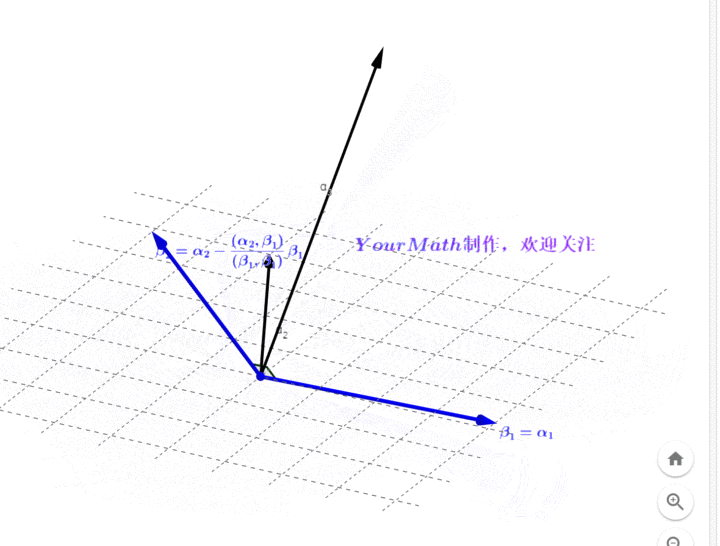
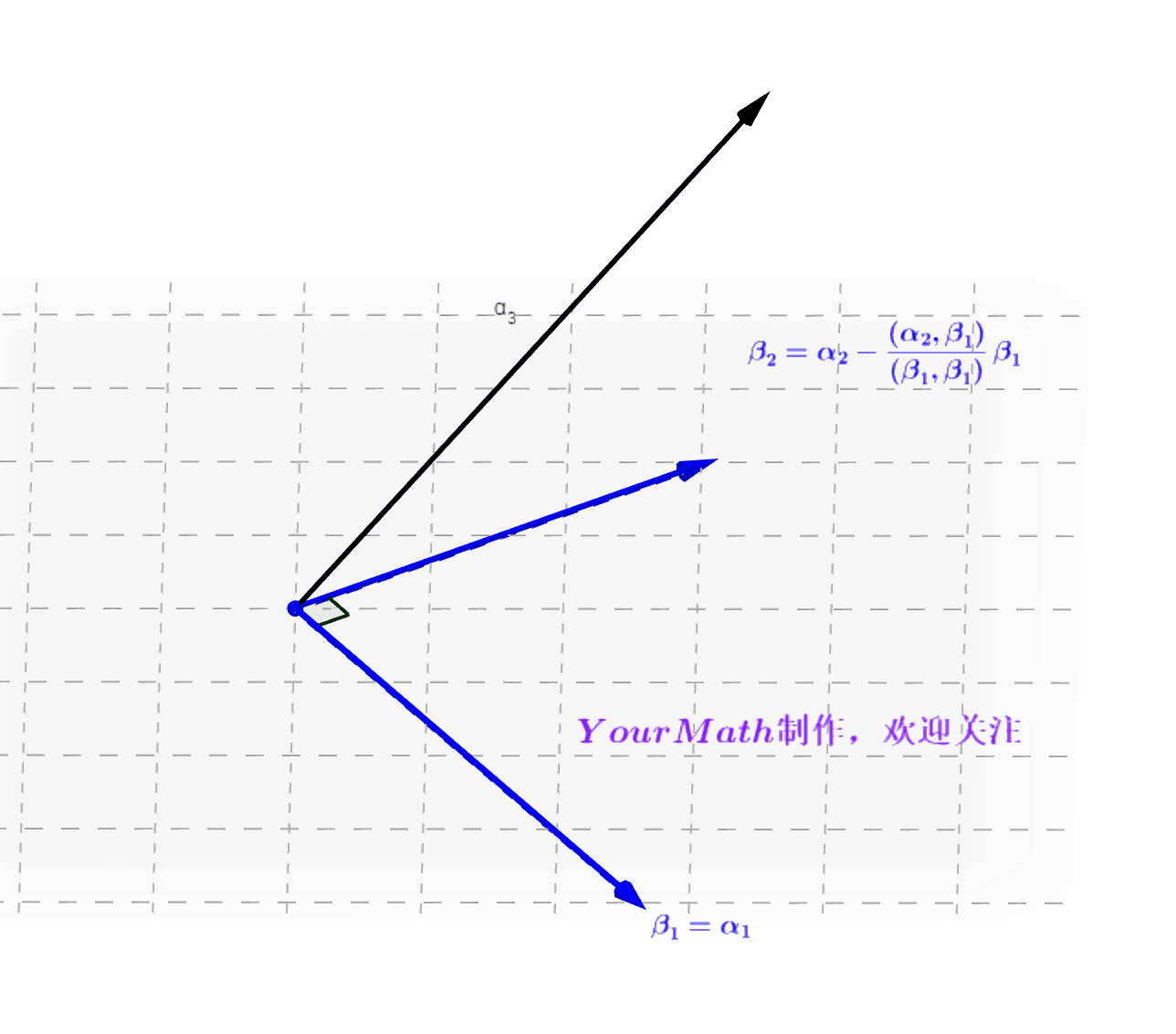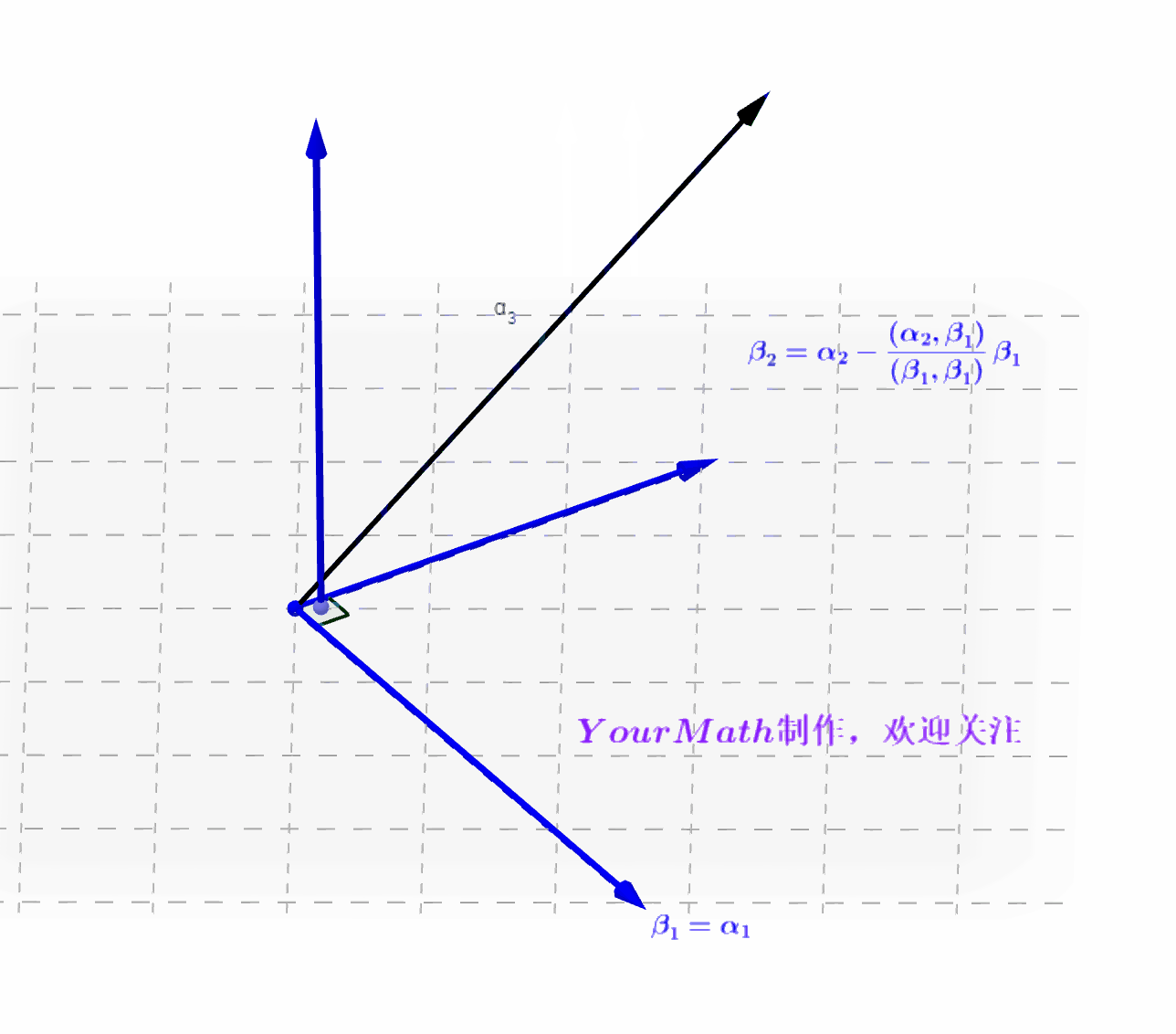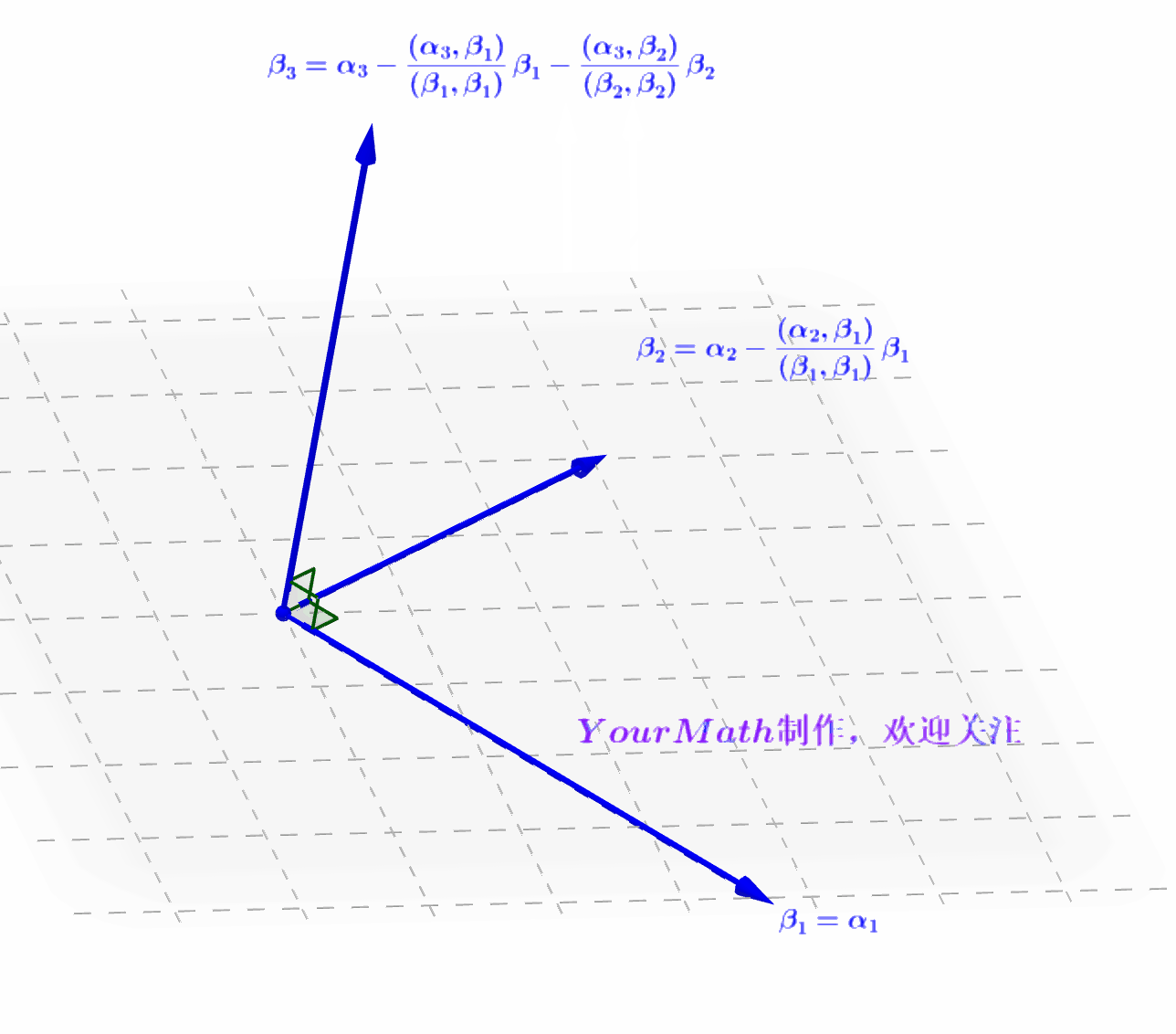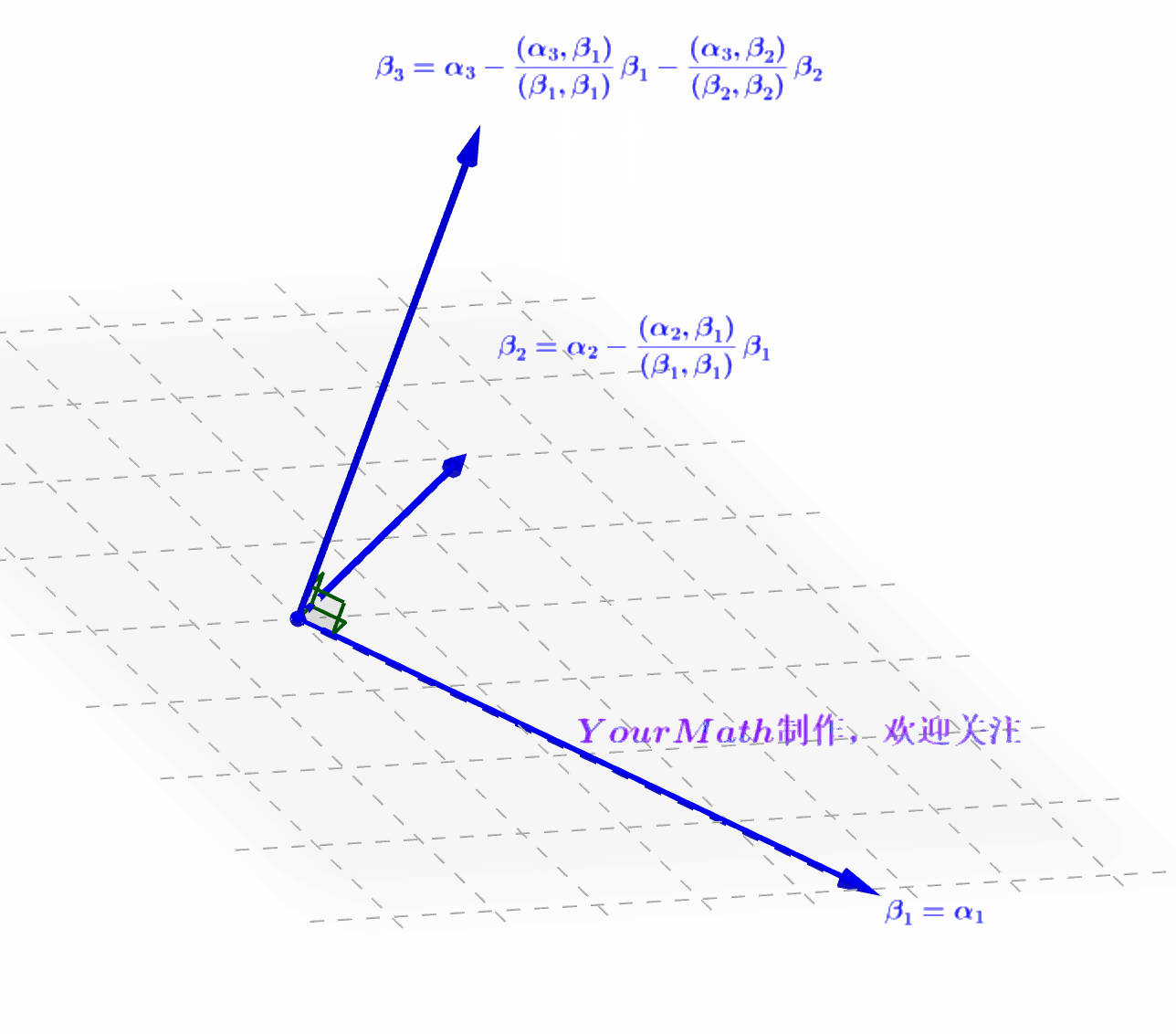
• 下面我们看看如何利用施密特正交化法将这一组基正交化。
  • Step1：令

• • Step2: 做向量
    在向量
    的投影，并与
    做差得到

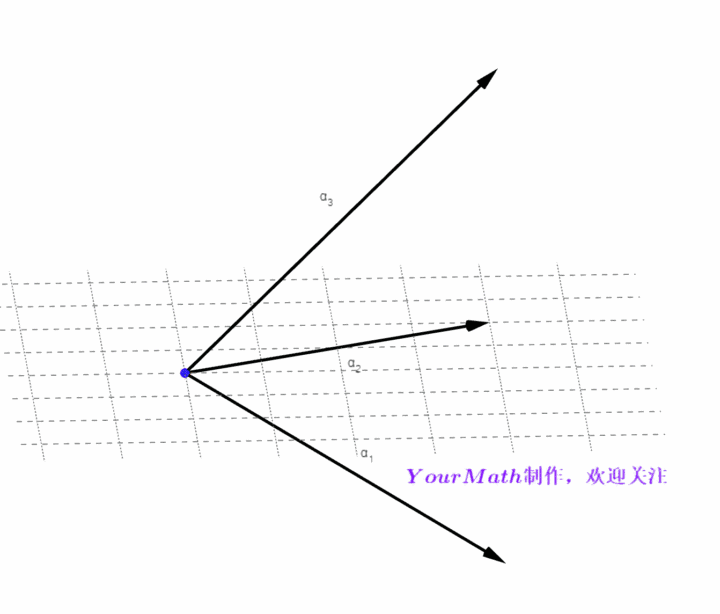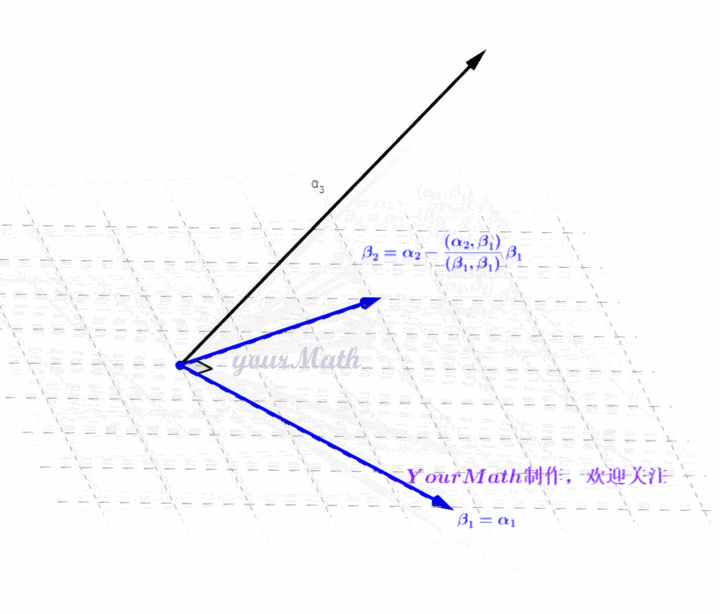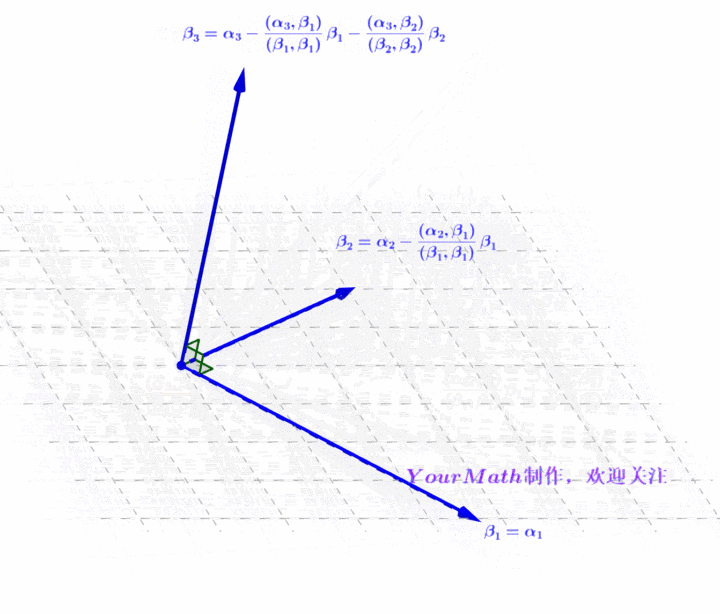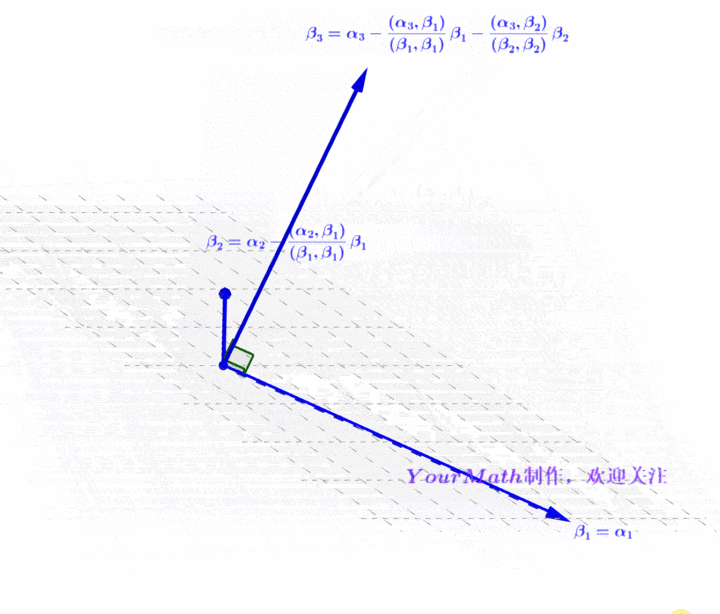
• • Step3：分别做向量
    在向量
    的投影
    ，利用
    减去两个投影的和得到

维欧氏空间的情况

• 对于任意一个
  维欧氏空间来说，我们也可以轻松得到一组基
  • Step1: 任意取一个非零向量
  • Step2: 除去非零向量
    所生成的子空间
    后，任意取一个非零向量
  • Step3: 除去非零向量
    所生成的子空间
    后，任意取一个非零向量
    。
  • Step4: 除去非零向量
    所生成的子空间
    后，任意取一个非零向量
    .
  • ...

因为空间维数有限，到第

步后一定可以产生

维欧氏空间的一组基。

• 利用施密特正交化找到一组正交基的过程与三维空间是类似的：
  • Step1：令
  • Step2: 做向量
    在向量
    的投影，并与
    做差得到
  • Step3： 分别做向量
    在向量
    的投影
    ，利用
    减去两个投影的和得到

• • Step4:分别做向量
    在向量
    的投影
    ,
    利用
    减去两个投影的和得到

• • ....

---

如果你想得到一个单位直角坐标系，或者单位正交基，那么你还需要对得到的正交向量逐个单位化即可。